输出自然数-第10届蓝桥杯国赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第7讲。
输出自然数,本题是2019年5月25日举行的第10届蓝桥杯青少组Python编程国赛真题,题目要求编程根据给定条件按照从小到大的顺序输出10个最小的自然数。
先来看看题目的要求吧。
一.题目说明
编程实现:
按照从小到大的顺序输出符合以下条件的10个最小的自然数:
它们是质数,且被3除余2,且被7除余6,且被11除余10,且被17除余16,且被23除余22。
输入描述:
无
输出描述:
10行,每行一个符合题目要求的自然数,按从小到大的顺序输出
评判标准:
-
30分:可以输出第一个符合题目要求的自然数;
-
50分:完全符合题目要求,即按照从小到大顺序输出了符合题目要求的10个自然数。
二.思路分析
这是一道计算的题目,涉及到的知识点包括循环语句、条件语句、余数运算以及质数的判断。
根据题意,可以将本题拆分成两个问题:
-
判断质数
-
余数的判断
首先是质数的判断,关于这部分的知识点,可以参考《包含3的数字-第10届蓝桥杯省赛Python真题精选》这篇文章,其中有详细的介绍。
需要注意的是,由于本题涉及的数字比较大,一定要使用效率更高的方法来判断质数。
余数的判断,则相对要简单多了,只需要使用%运算符即可。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们分两步来编写代码:
-
定义函数判断质数
-
输出10个自然数
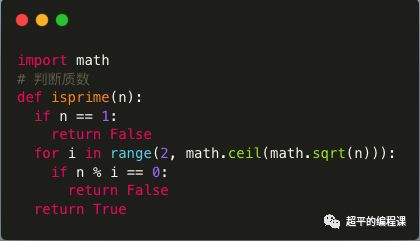
1. 定义函数判断质数
参考《包含3的数字-第10届蓝桥杯省赛Python真题精选》中的思路分析,定义函数如下:
需要注意的是,这里使用了math库中的ceil()方法,其作用是向上取整。为什么要向上取整呢,原因在于range()函数具备虎头蛇尾(有头无尾)的特点。
当然,你也可以使用int()函数保留整数部分,然后再增加1。
2. 输出10个自然数
有了上面定义的函数,接下来就简单多了,使用循环,找到前10个满足条件的质数即可。但是,我们需要考虑一个问题,可以使用for...in循环吗?
仔细思考,你会发现无法直接确定这10个数字的范围是多少。针对这种情况,可以改用while循环,并使用一个计数器,来记录输出自然数的个数,它可以作为循环的条件。
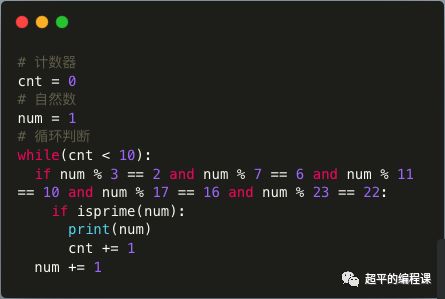
根据这个思路,编写代码如下:
代码比较简单,但是必须要强调一点,就是判断的写法和顺序。
题目是这么描述的,“它们是质数,且被3除余2,且被7除余6,且被11除余10,且被17除余16,且被23除余22。”
很多同学会自然而然地先判断是否为质数,再判断余数的情况。如果你这么写,那么输出10个自然数需要很长的时间,为什么呢?
原因很简单,由于数字跨度大,判断素数是非常消耗时间的。
所以比较好的方法,是先判断余数情况,再判断是否为质数,这样可以节省很多不必要的判断,极大地提升了效率。
运行程序,执行结果如下:
1083851216770328902713793481433540746966916141827632246970450377225679
至此,整个程序就全部完成了。
四.思考与总结
本题分数为50分,代码在20行左右,涉及到的知识点包括:
-
循环语句,包括for...in循环和while循环;
-
条件语句,主要是if语句及嵌套用法;
-
运算符的灵活使用,包括%和and;
-
数学函数库的使用;
-
函数的定义及使用;
题目难度一般,重点有两个,一是质数的判断,二是while循环的灵活运用。这些都是非常基础的Python编程知识,对于大部分同学都没有问题。
真正关键的是,如何提升程序的效率,在蓝桥杯比赛中,对程序运行的时间是有要求,一旦超时,是不能得分的。
所以,我们不仅要把程序写出来,还要想办法写得更好。一定要有优化思维,先保证写出来,然后在此基础上进行优化,提升程序的效率。
比如本题中质数的判断以及自然数的判断,无非都是使用枚举算法逐个处理,那么优化的思路就是能否去掉一些不必要的判断,让枚举的规模降低,从而提升效率。
计算机解决问题其实没有任何特殊技巧,它唯一的解决办法就是枚举,穷举所有的可能性。
而算法设计无非就是:
-
先思考如何枚举
-
再追求聪明的枚举
超平老师给你留一个思考题,关于质数(素数)的判断,除了本题中给出的算法,还有效率更高的算法吗,具体是怎么实现的呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香
需要源码的,可以移步至“超平的编程课”gzh。