博弈论入门

目录

什么是博弈？

博弈论的发展历史？

博弈的要素有哪些？

博弈的分类？

博弈论的应用

收益矩阵

纳什均衡的定义

博弈论的例子

1、田忌赛马

2、穷途困境

2.1优化反应函数法

2.2Nashpy库

2.3顶点枚举算法

3、Nash游戏

4、巴什博奕（Bash Game）

5、威佐夫博弈（Whthoff Game）

6、电子商务中的定价策略

---

什么是博弈？

概念1：博弈是指在一定的游戏规则约束下，基于直接相互作用的环境条件，各参与人依靠所掌握的信息，选择各自策略（行动），以实现利益最大化和风险成本最小化的过程。简单说就是人与人之间为了谋取利益而竞争。

概念2：博弈是指在平等的对决中参与双方分别根据对方的策略指定自己的应对策略，从而取得胜利。

博弈论的发展历史？

博弈论的发展历史可以追溯到两千多年前的中国和古希腊，最早的博弈案例包括《孙子兵法》、《孙膑兵法》、《三十六计》、《六韬》等书籍中的故事。然而，博弈论真正成为一门系统的学科，是在20世纪初。

在20世纪20年代，法国数学家波莱尔首次用数学语言刻画了博弈问题，提出了“策略”和“混和策略”概念，并用最佳策略和概念研究了下棋等决策问题。同时，德国哲学家和数学家莱布尼茨在1710年就预言了关于策略博弈理论出现的必要性和可能性。

随后，在1928年，约翰·冯·诺依曼与奥斯卡·摩根斯坦合作出版了《博弈论与经济行为》，标志着博弈论的正式诞生。他们提出了两人零和博弈的极小极大定理，并证明了博弈论的基本定理。

在20世纪50年代，博弈论发展到了鼎盛时期，包括纳什、海萨尼和泽尔腾等人在内的众多学者做出了重要贡献。纳什提出了“纳什均衡”的概念，海萨尼和泽尔腾等人也在合作博弈领域做出了重要贡献。

自那时起，博弈论在经济学、政治学、生物学等多个领域得到了广泛应用。尤其是经济学领域，许多学者如纳什、海萨尼和泽尔腾等，在博弈论领域做出了重要贡献。1994年，纳什、海萨尼和泽尔腾因在博弈论领域的突出贡献获得了诺贝尔经济学奖。

博弈论在军事战略、国际关系、法律等领域也有着广泛的应用。它提供了一种方法来理解和预测在特定环境中的行为结果，帮助人们制定出最优策略。

博弈的要素有哪些？

参与者：至少有两个参与者，他们之间存在相互依赖的关系。

策略集：每个参与者都有一套完整的策略集，定义了在不同状态下他们可以选择的行动。

效用函数：衡量参与者在每一组策略组合下的收益，参与者总是愿意选择高收益而不是低收益。

信息：参与者根据他们所掌握的信息做出决策。

博弈的分类？

博弈可以根据不同的标准进行分类，以下是一些常见的分类方式：

按照参与人数分类：可以分为单人博弈、双人博弈、多人博弈。

按照策略数量分类：可以分为有限策略博弈和无限策略博弈。

按照参与人对其他参与人的了解程度分类：可以分为静态博弈和动态博弈。

按照其他因素分类：例如，按照博弈中的得益分类，可以分为零和博弈、常和博弈、变和博弈；按照参与人之间是否合作分类，可以分为合作博弈和非合作博弈等。

此外，根据博弈的研究范式和研究方法的不同，博弈论还可以分为传统博弈论和演化博弈论等。

博弈论的应用

博弈论在许多领域都有广泛的应用，如生物学、经济学、国际关系、计算机科学、政治学、军事战略等。在经济学中，博弈论已经成为标准分析工具之一，生物学家使用博弈理论来理解和预测进化论的某些结果。

此外，博弈论也可以被视为一种思维方式和决策方法。它帮助人们分析问题，找到最优策略，以及理解和预测他人的行为。在商业、政治和日常生活中，博弈论都有广泛的应用，如商业策略、国际关系分析、法律和政策制定等。

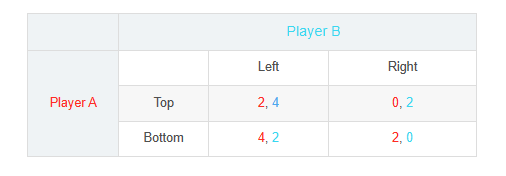
收益矩阵

有两名玩家A 和 B ，每个玩家都有两种策略，A 可以选择“TOP”或者“Bottom”，B 可以选择“Left”或者“Right”。做出不同的行为所对应的收益也是不同的。将二者的收益整理成如下矩阵，A的策略在左边，红色表示A的收益；B的策略在上边，蓝色表示B的收益。

纳什均衡的定义

在博弈论中，纳什均衡是指在博弈中所有参与者都采取最优策略的状态。具体来说，如果在一个博弈中，每参与者都选择了一种策略，且没有任何一个参与者可以通过改变自己的策略来获得更好的结果，那么这个状态就是一个纳什均衡。

纳什均衡可以分成两类：“纯策略纳什均衡”和“混合策略纳什均衡”。

纯策略（pure strategies）指的是如果一个策略规定参与人在每一个给定的信息情况下只选择一种特定的行动，称为纯策略，简称“策略” ，即参与人在其策略空间中选取唯一确定的策略。纯策略纳什均衡指的是，参与人采用纯策略确定的均衡。

混合策略（mixed strategies）指的是如果一个策略规定参与人在给定的信息情况下以某种概率分布随机地选择不同的行动，称为混合策略。参与人采取的不是明确唯一的策略，而是其策略空间上的一种概率分布。混合策略纳什均衡指的是，参与人采用混合策略确定的均衡。

博弈论的例子

1、田忌赛马

齐国大将田忌很喜欢赛马。他和齐威王约定，进行一次赛马比赛。他们各自将自己的马分为上、中、下三等，依次派出上等马、中等马和下等马，进行三轮比赛。由于齐威王每个等级的马都比田忌强，三场比赛下来，田忌都失败了。田忌军师孙膑帮他想了一个对策，建议田忌调整赛马顺序，先用下等马对齐威王的上等马，再拿上等马对齐威王的中等马，最后拿中等马对齐威王的下等马，三局两胜，以弱胜强，反败为胜！

以下为单次对决的代码：

import nashpy as nash
import numpy as np
'''
假设田忌有3匹马（A、B、C），
齐王有4匹马（a、b、c）
Aa上等马
Bb中等马
Cc下等马
'''
tianji_strategies = ["A", "B", "C"]
qiwang_strategies = ["a", "b", "c"]
tianji_payoff = np.array([[-1, 1, 2],
                         [-2, -1, 1],
                         [-3, -2, -1]])
​
qiwang_payoff = np.array([[1, -1, -2],
                          [2, 1, -1],
                          [3, 2, 1]])
​
game = nash.Game(tianji_payoff, qiwang_payoff)
equilibria = game.support_enumeration()
for eq in equilibria:
    print("纳什均衡策略组合：", eq)
# #重复博弈
# for _ in range(3):
#     game = nash.Game(tianji_payoff, qiwang_payoff)
#     equilibria = game.support_enumeration()
#     tianji_payoff, qiwang_payoff = qiwang_payoff, tianji_payoff # 交换角色
# print(list(equilibria))

纳什均衡策略组合：(array([1., 0., 0.]), array([1., 0., 0.]))

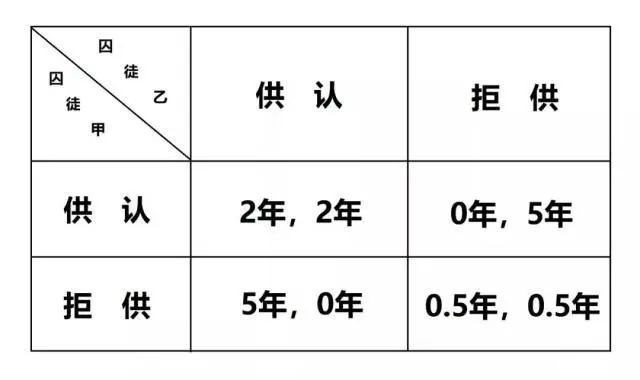
2、穷途困境

两个人因盗窃被捕，警方怀疑其有抢劫行为，但未获得确凿证据可以判他们犯了抢劫罪，除非有一个人供认或两个人都供认。即使两个人都不供认，也可判他们犯盗窃物品的轻罪。犯罪嫌疑人被分离审查，不允许他们之间互通消息，并交代政策如下：如果两个人都供认，每个人都将因抢劫罪加盗窃罪被判2年监禁；如果两个人都拒供，则两个人都将因盗窃罪被判处半年监禁；如果一个人供认而另一个拒供，则供认者被认为有立功表现而免受处罚，拒供者将因抢劫罪，盗窃罪以及抗拒从严而被重判5年。

2.1优化反应函数法

import numpy as np
​
# 定义博弈矩阵
A = np.array([
    [[-2, -2], [0, -5]],
    [[-5, 0], [-0.5, -0.5]]
])
​
# 计算最优反应函数
def best_response(A,i):
    j = 1 - i
    return np.unravel_index(np.argmax(A[i, :, j]), A.shape[:2])[0]
​
# 计算纳什均衡
br1 = best_response(A, 0)
br2 = best_response(A, 1)
if A[br1, br2, 0] == A[br1, br2, 1]:
    print(f'({br1}, {br2}) is a Nash equilibrium')
else:
    print('No Nash equilibrium')

(0, 0) is a Nash equilibrium

0-供认，1-拒供

甲乙都供认

2.2Nashpy库

纯策略

import numpy as np
import nashpy as nash
A = np.array([[-2, 0], [-5, -0.5]])
B = np.array([[-2, -5], [0, -0.5]])
game = nash.Game(A, B)
eqs = game.support_enumeration()
for eq in eqs:
    eq_left, eq_right = eq
    expected_payoff_left = np.dot(eq_left, A).dot(eq_right)
    expected_payoff_right = np.dot(eq_left, B).dot(eq_right)
    print("左方策略：", eq_left, "，右方策略：", eq_right, "，左方期望效用值：", expected_payoff_left, "，右方期望效用值：", expected_payoff_right)

左方策略：[1. 0.] ，右方策略：[1. 0.] ，左方期望效用值：-2.0 ，右方期望效用值：-2.0

0-供认，1-拒供

甲乙都供认，即刑期2年，

混合策略

import nashpy as ns
import numpy as np
​
A = np.array([[2, 0], [5, 0.5]])
B = np.array([[2, 5], [0, 0.5]])
payoff = ns.Game(A, B)
​
r = np.array([.5, .5])  # A玩家对应策略概率
c = np.array([0.7, 0.3])  # B玩家对应策略概率
​
payoff = ns.Game(A, B)
print(payoff[r, c])

[-2.525 -1.525]

甲以0.5的概率选这供认，0.5的概率选择拒供，收益2.525年刑期

甲以0.7的概率选这供认，0.3的概率选择拒供，收益1.525年刑期

2.3顶点枚举算法

import numpy as np
​
# 两个玩家的收益矩阵
A = np.array([[2, 0], [5, 0.5]])
B = np.array([[2, 5], [0, 0.5]])
​
# 玩家策略空间
strats_A = [0, 1]
strats_B = [0, 1]
​
def vertex_enumeration(A, B, strats_A, strats_B):
​
    equilibria = []
​
    # 枚举所有顶点
    for s_A in strats_A:
        for s_B in strats_B:
​
            # 计算最优响应
            br_A = np.argmax(A[s_B, :])
            br_B = np.argmax(B[:, s_A])
​
            # 判断均衡
            if s_A == br_A and s_B == br_B:
                equilibria.append((s_A, s_B))
​
    return equilibria
​
print(vertex_enumeration(A, B, strats_A, strats_B))

[(0, 0)]

3、Nash游戏

裁判拿出n个棋子，n可能很多。你和对手轮流取子，规则是：

当n是奇数时，你和对手都只容许拿走1颗棋子，

n是偶数时，有两个选择：拿走一个，或拿走一半，由自己判断选择采取哪一种做法。取胜的条件是：拿走棋子数量最多的取胜或没有棋子拿的失败。

4、巴什博奕（Bash Game）

一堆n个物品，两个人轮流从中取出（1~m）个，轮到谁取时发现物品没有了，判定该玩家输。

def bash_game(n, m):
    # 判断当前轮到的玩家是否处于必胜状态
    if n % (m + 1) == 0:
        return "后手必胜"
    else:
        return "先手必胜"
​
# 输入物品数量n和每轮最多取出的数量m
n = int(input("请输入物品数量n："))
m = int(input("请输入每轮最多取出的数量m："))
​
# 调用函数并输出结果
result = bash_game(n, m)
print(result)
​

5、威佐夫博弈（Whthoff Game）

有两堆各若干个物品，两位玩家轮流从任意一堆中取出至少一个或者同时从两堆中取出同样多的物品，规定每次至少取一个，至多不限（两堆不一定一样多），轮到谁取时发现物品没有了，判定该玩家输。

6、电子商务中的定价策略

两家公司A和B在网上销售同一产品。公司A可以选择以10美元或20美元的价格出售其产品,而公司B可以选择以10美元或15美元的价格出售其产品。给出每家公司的最优定价策略？

参考文献1、https://nashpy.readthedocs.io/en/stable/text-book/index.html2、《哈林顿博弈论》，哈林顿，中国人民大学出版社3、《用博弈的思维看世界》，蒋文华，浙江大学出版社