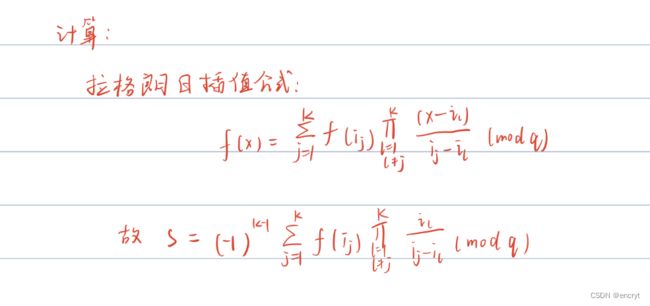论文阅读-Practical Secure Aggregation for Privacy-Preserving Machine Learning（谷歌.CCS.2017）

实用的用户隐私机器学习安全聚合的算法

1.前置知识

门限机制和Shamir秘密共享

秘密s通过某种方案被分成n个部分，每个部分被称为份额或者影子，由一个参与者持有，使得：

1. 由k个或多于k个参与者所持有的部分可以重构S
2. 由少于k个参与者所持有的部分则无法重构S

该方案称为（k,n）秘密分割门限方案，k称为门限值

shamir于1979年，基于多项式插值算法设计了shamir(t,n)门限共享体制，他的秘密分配算法如下：

组成：

• 份额分配算法
• 恢复算法

Shamir门限方案的构造思路：

例子：（3，5）门限方案

安全多方计算|基于shamir秘密共享方案

Diffie-Hellman密钥交换协议

公钥加密算法加解密复杂，花费的时间久，加解密数据时使用对称加密算法，密钥管理使用公钥密码技术；

Diffie-Hellman密钥交换算法利用的是离散对数的难解问题。

2.Practical Secure Aggregation for Privacy-Preserving Machine Learning

论文信息：CCS 2017 谷歌

1.introduction

主要内容就是提出了安全求和，用在联邦学习场景下从多个客户端场景下对每个客户端的梯度进行汇聚；

问题定义为：有m个客户端C1…Cm,每个客户端都有自己的私密数据Xi，业务需求求出客户端的总和，然后发送给服务器，同时还要满足安全型的需求，即不能向其他客户端泄露数据Xi。

应用场景：手机作为客户端，需要考虑两个问题，第一是通信开销，第二是解决掉线问题；

本文提出两种模型：

1. plain model：效率高，可以抵抗HBC攻击者
2. random oracle model：可以更加保护隐私，抵抗主动攻击;但是需要额外的一轮时间

2.SECURE AGGREGATION FOR FEDERATED LEARNING

为啥需要安全聚合，需要满足的要求：

1. 处理高纬度向量
2. 通信高效
3. 对掉线鲁棒
4. 较高的安全特性

3.CRYPTOGRAPHIC PRIMITIVES

3.1Secret Sharing

采用shamir的（t,n）门限值方案，参数在一个有限域F上，有一个大素数p生成；
$$SS.share(s,t,U)->\{(u,s_u){\}}_u\in U；s秘密信息，U全体用户，u得到秘密的用户$$

表示把秘密s分享给用户，每个人的秘密份额是Su
$$SS.recon(\{(u,s_u){\}}_u\in v,t)->s$$
表示给定一定系列用户(大于等于门限值t)和秘密份额以及阈值t,就可以重构秘密s;

3.2Key Agreement

a tuple of algorithms (KA.param,KA.gen,KA.agree)

KA.param(k)->pp 公共参数
$$KA.gen(pp)->(s_u^{SK},s_u^{PK})$$
允许任何一个用户去产生属于自己的公私钥对；
$$KA.agree(s_u^{SK},s_v^{PK})->s_{u,v}$$
用户u可以结合自己的私钥和对方的公钥得到一个秘密信息s（属于u和v之间的）;

本文采用的是Diffie-hellman密钥交换协议：
$$KA.param(k)->(G^{\prime },g,q,H)$$
生成素数q的群G‘ ，生成元为g，同时给定一个哈希函数
$$KA.gen(G^{\prime },g,q,H)->(x,g^x)$$
选取x作为私钥，g^x作为公钥
$$KA.agree(x_u,g^{x_v})->s_{u,v}计算s_u,v=H((g^{x_v}{)}^{x_v})$$

$$经过三个操作，共享数据可以只要只有他们两个知道的随机数S_{u,v}=s_{v,u}$$

3.3Authenticated Encryption

在认证和传输消息（两方交换信息的时候）的过程中可以保证机密性和完整性；

三个操作：

1. 密钥生成算法，生成密钥c
2. AE.enc(c,x)->y,密钥c对数据x进行加密
3. AE.dec(c,y)->x，用密钥c对密文y解密

3.4Pseudorandom Generator

给定一个种子，生成随机数，虽然是靠公式生成，但是和真随机的字符串不可区分，所以叫伪随机数生成器；

3.5Signature Scheme

$$
SIG.gen(k)->(d^{PK},d{sk}) 表示生成公私钥对

$$

$$SIG.sign(d^{sk},m)->s表示利用私钥对m进行签名$$

$$SIG.ver(d^{SK},m,s)->\{0,1\},通过公钥对签名进行认证，并与源数据m进行对比确定验证是否通过$$

3.6Public Key Infrastructure

为了防止服务器模拟任意数量的客户端（在主动对抗模型中），需要一个公钥基础设施的支持，允许客户端注册身份，并使用他们的身份签署消息，这样其他客户端可以验证此签名；
PKI 是用来实现基于公钥密码体制的秘钥和证书的产生、管理、存储、分发和撤销等功能的集合。这样各种基于秘钥的算法就能很容易地运行了。

4 .TECHNICAL INTUITION（技术出发点）

$$U代表全体用户，u代表其中的一个用户，x_u表示每个用户的私有数据，\sum _{u\in U}{x}_u需要求的目标$$

4.1Masking with One-Time Pads

第一种构造就是加入每个用户自己的数据Xu经过一个特殊的编码，假设一对用户（u，v）协商出一个秘密Su，v,u加上这个值，v减去这个值，那么总和就是不变的:

有两个shortcomings ：

1. 怎么协商随机数
2. 某个客户端突然掉线

4.2 Efficient Communication andHandling Dropped Users

1.使用Diffie-hellman密钥协商，协商出来一个密钥种子，给PRG，并借助PRG来减少通信开销，产生协商出的随机数

2.使用shamir的（t,n）门限方案，我们可以认为每个客户把Su,v采用秘密分享的方式发出去了，并且只要t个客户端在线就可以还原除秘密信息Suv，这样就可以解决掉线的问题；（实际上，分发的是公钥的share，然后根据公钥和v的数据，可以算出来Su,v）
但是这样仍然存在问题，就是加入说用户u的数据不是掉线，而是因为网络延迟导致的，这样服务器是可以通过已经收到的其他用户的数据来计算出用户u的数据的；

4.3Double-Masking

上面存在的问题可以通过引入一个新的随机数b，把这个随机数和数据绑定，就是这样：
每个用户u在生成Su,v的期间对附加种子bu进行采样，秘密共享回合期间，用户还生成bu的份额并将其分发给其他每个用户。

在分发阶段，随机数b和s均采用秘密分享的方案分发出去，并且保证t个用户就可以恢复；

在恢复阶段，对于一个诚实的用户v，他不会把bu和Su,v同时说出去，如果用户u掉线了，那么v会说出Su,v，如果用户u在线，那么v会说出bu；

因为采用了两类随机数，所以这个方法也叫做Double-Masking；
整体步骤如下所示：

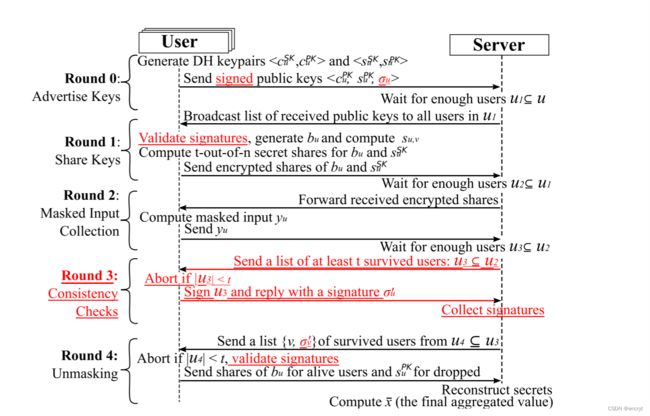
红色的代表要抵抗主动攻击对手所要做的必要的步骤；

5 .A PRACTICAL SECURE AGGREGATION PROTOCOL

$$有n个用户，四轮，每个用户u有自己的向量x_u（都是等长的数据）$$

$$任何一方在任何时候都可以停止发送信息，只要有t个人能存活到最后一轮，协议就可以正常运行$$

总的协议如下：红色的代表要抵抗主动攻击对手，需要额外的签名和一个PKI；


下面仔仔细细的分析每一轮：针对HBC的方案
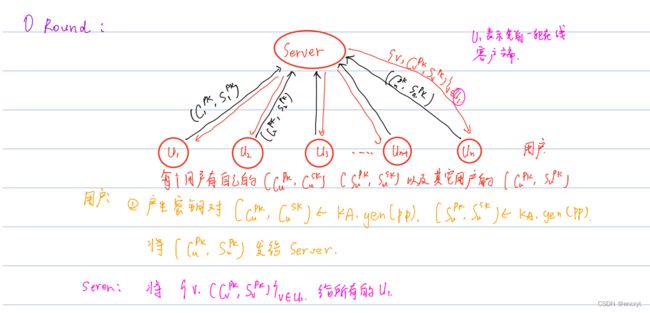
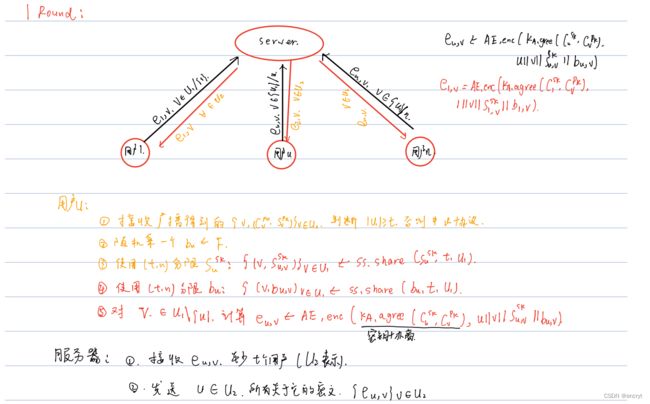
1.设置阶段：

2.Round0：

3.Round1：

4.Round2：

5.Round4：

针对抵抗主动攻击的防御，就是在原来HBC的基础上，增加一个数字签名个PKI的设施，具体的看方案很容易理解，这里不细说，在安全性分析里会说；

6.SECURITY ANALYSIS

请看另一篇文章；