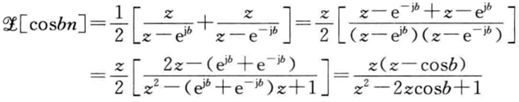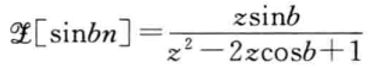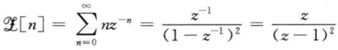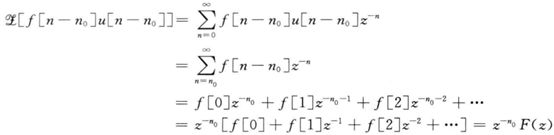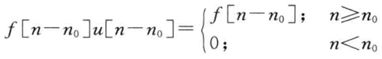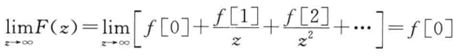信号与系统复习归纳（十一）：Z变换+例题

对象：离散时间系统
过程：差分方程——z变换——复频域模型（代数方程）——系统特性
类比微分方程用LT，也是使得计算简化。
逆z变换：变回离散时间变量

1 ZT的定义

这部分内容和LT的非常像

1.1 ZT的类型和定义

（1）双边ZT（下标带b）

z是一个复数，用Σ+jΩ表示。
（2）单边ZT
根据双边ZT拆开

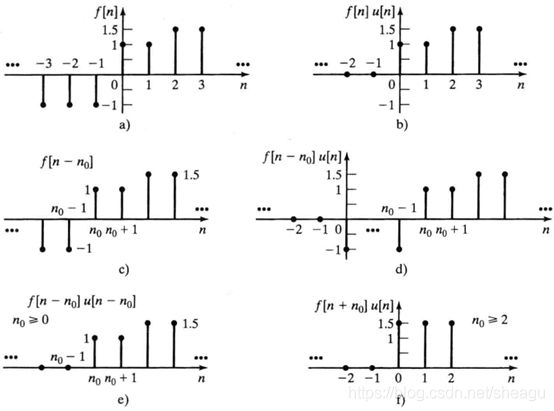
规定f[n]在n<0的时候是0，那么只剩下右边的，即：

单边ZT简称ZT。

1.2 IZT

（1）用反演积分定义

积分路线是Γ，它是z平面的逆时针闭合积分路线。但一般不这么算，太烦了，查表。
单边的逆z变换形式和这个一样，得到的结果是f[n]，它是整个时间轴上的函数，但是规定n<0的时候是0。
（2）用部分分式展开法求
对于下面的例子

右边是两个分数相乘，只要分子的次数不大于分母，它一定可以拆开为

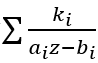
的形式，所以右边的分子是二次、一次、零次都可以。现在是二次的，按理说可以直接拆开，但拆完以后每个分子都是常数，而这个形式在ZT表上查不到，表上的都是分子是一次的。所以，在进行拆分之前，需要拿走一个z，等拆完后再乘上去，分子的次数就升到了一次，方便用ZT表了。即：

再求系数

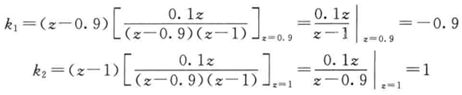
因此

利用z/(z-a)的IZT很容易得到

（3）用长除法展成幂级数求
适用于只需要知道y[n]的前几项的时候。因为长除法不一定能找到规律，可能写不出级数的表达式。

进行降幂长除：

得到：

（4）有复数极点的情况
当然可以用（2）的方法求，但是最后的形式是：系数是复数，函数是复数，虽然它们加起来之后虚部会相互抵消，结果仍然是实数，但是看起来复杂。这里的方法可以把逆变换直接表示成实函数的和。
对于下面这个实函数：

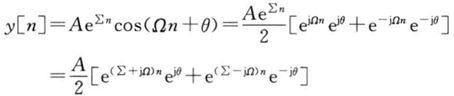
第一个表达式是实数形式的，我们的目标就是从后面两个复数形式，推得它。关键就在于求A、Σ、Ω、θ。
查表得到y(n)的ZT（星号表示共轭，注意e^(jθ)是常数，直接拎出来）：

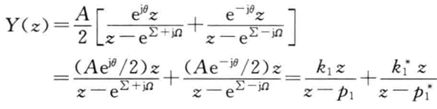
利用下面的关系：

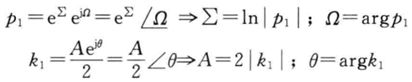
对于一个已经得到的Y(z)，我们知道的是k和p，再通过p计算Σ和Ω，通过k求A和θ，就得到了这四个系数，可以还原成实数的表达式了。
比如：


因为


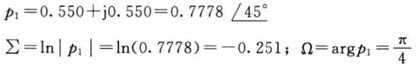
所以

1.3 可以进行ZT的条件和收敛域

f(n)能够使得

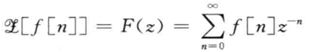
收敛。
因为n无穷的时候，z^(-1)越来越小，所以z的幅值变大更可能收敛，即收敛于的形式一般是|z|>|r|，r由f(n)决定。
双边ZT的收敛域（ROC）必须考虑。

2 常见函数的ZT

级数在用闭式函数表示ZT的时候很有用。闭式函数：由初等函数经有限次初等运算复合而成。

2.1 阶跃函数

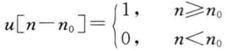
则

右边是一个级数：

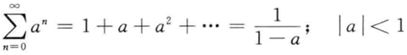
把a代成z^(-1)：

因此：

用ZT的定义求出来的相函数的自变量是z^(-1)，看着难受，可以写成：

2.2 指数函数

因此：

即

拓展：如果把a^n表示成

那么就可以得到

后面会用到。

2.3 冲激函数

因此

如果n_0=0，那么

2.4 三角函数

因为

所以

利用指数函数的ZT里的结论得到

同理

2.5 衰减振荡函数

所以

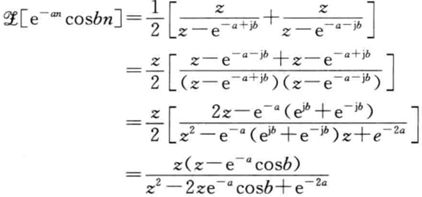
对比一下4和5：

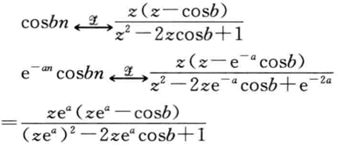
这里有一个一般规律（频域伸缩变换特性）：

因此，根据

可以得到

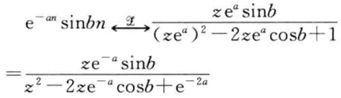
2.6 单位斜坡函数

根据幂级数求和公式

得到

即

2.7 总结

3 ZT的性质

3.1 线性变换

3.2 两个函数乘积的z变换~=两个函数z变换的乘积

3.3 时域平移特性

n_0>=0时

n_0<0时

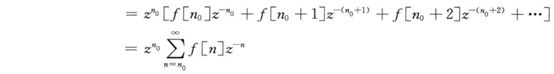
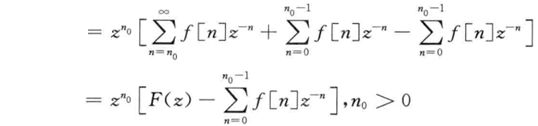
（1）求解差分方程
对于一个α数字滤波器（低通）

进行ZT：

因此

这是差分方程的第三种解法。前面用过的还有经典解法、迭代解法。
定义传递函数为

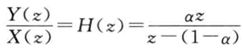
用来表示LTIDT系统

（2）规定α=0.1，求这个滤波器的单位阶跃响应
输入阶跃信号的ZT为

因此

再进行IZT就可以得到y(n)了。但是这个Y(z)比较复杂，可以用部分分式展开，先化成查表能查到的形式。同时右边的分子次数比较高，先除过去：

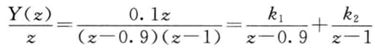
待定系数求得

因此

再查表

（3）对比不同的平移


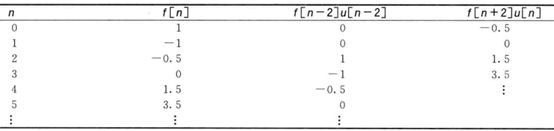
从第三个可以看出，两个离散间隔的时间提前，使得最初的两个采样值丢失。
符合

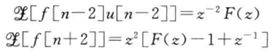
3.4 频域伸缩变换特性/调制特性

左边乘以e^ (-an)，导致 z平面上发生伸缩变换e^ a：a可以是复数，从复数的角度考虑，e^a可以写成模乘以(cos+jsin)的形式，相当于长度变化+角度变化。

3.5 复移位特性

可以从频域伸缩变换特性推。

3.6 初值定理

根据F(z)，直接得到f(0)，不需要再进行IZT

即

3.7 终值定理

根据F(z)，直接得到f(n)的稳态值

使用条件：f[n]的终值，即f[∞]存在（代进去看看就知道了）。一般来说，如果F(z)在单位圆内，除了z=1外仅有单个极点，那么f[0]的终值存在，而且只有在z=1处含有单个极点才能使终值不为0。

3.8 尺度变换

k为正整数时

m=n/k即n=mk会产生额外的样本值，将所有额外的样本值设为0。
相反，如果是f[nk]，k为正整数，那么会导致样本值的丢失。

3.9 时域卷积定理

3.10 总结

4 ZT的作用：分析LTIDT系统

4.1 用ZT求H(z)

适用对象：离散线性时不变系统
建模工具：线性常系数差分方程
用差分方程表示系统：

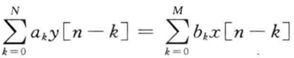
一般为了方便讨论，取M=N（多余的置零）：

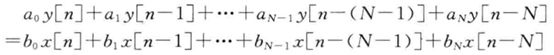
根据时间延迟特性：

得到ZT（这里是单边的ZT，要求信号是因果的，否则延迟特性不能这么用）：

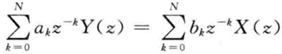
即

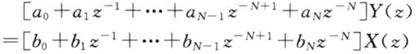
系统的传递函数：

这个式子和第10章推导的仅适用于复指数输入信号的传递函数相同，但可以用于任何一个可以进行ZT的信号，是第10章中传递函数的推广。
知道传递函数后，就可以用Y(z)=H(z)X(z)求响应了，用部分分式分解法，然后查表凑IZT啥的，前面有例子。

4.2 再从H(z)看系统性质

（1）因果性
对于一个时间提前单元（与后面时刻输入有关，非因果）

如果初态是0，那么

得到

这是时间提前单元的传递函数。在初态为0的假设下，N个级联的效果是

如果有N个延迟单元，那么传递函数是z^(-N)。
如果H(z)就是上面的简单形式，那么从H(z)就可以一眼看出系统是不是因果的了。但是H(z)未必那么简单，比如它可能是复杂分数

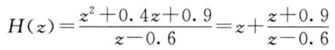
像这样的H(z)可以拆出整式，也就可以看成是两个系统的并联：一个是z时间提前，另一个是(z+0.9)/(z-0.6)，既然有提前的部分，它就是非因果的。实际上，只要分子的次数比分母高，系统就是非因果的。这是通过H(z)判断系统因果性。
疑问：我可以先装一个延迟单元，然后把它的输出接入提前单元，这样的系统虽然有提前单元，但也是可以实现的，从H(z)观察时，会不会因为分子次数高而判断错误？不会，因为延迟单元是z^(-1)，如果延迟单元的数目和提前单元的一样的话，分子分母就约分约掉了，不影响H(z)的表达式。其实应该这么表述：如果系统的提前单元个数多于延迟单元的个数，那么它的H(z)的分子次数会高于分母次数，它是非因果的，不可实现的。
对于z的次数是负数的表达式

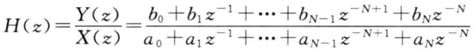
则如果a_0=0，那么系统是非因果的。
（2）BIBO稳定性
定义：对于每一个有界输入，都有有界输出。一定是“每一个”，如果输入无穷多个，叠加起来的效果就不好说了；也一定是“有界输入”，否则如果输入是无穷的，输出很难有界，用无穷输入来批评某个系统不稳定是不公平的。
对于下面的传递函数

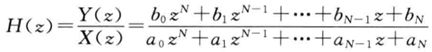
分解分母多项式得到：

它的解就是极点p，如果z取这些值，输出就是无穷的，肯定不稳定。
如果H(z)的极点没有重根（这里只是方便讨论，后面得到的BIBO稳定性条件也是适用于有重根情况的），则输出可以表示为

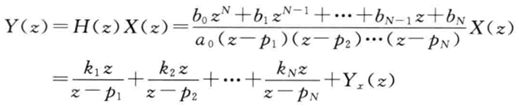
其中Y_x(z)表示展开的部分分式中源于输入信号X(z)极点的分式之和。因此，Y_x(z)表示强迫响应分量。这里可能比较抽象，举个例子：
比如，H(z)是这个：

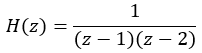
而输入信号是这个：

系统的极点是1和2，输入的极点是3。输出是：

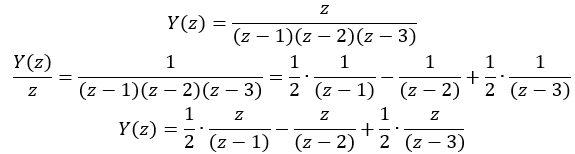
它的第三项就是所谓的Y_x(z)，是强迫响应分量。其实从分式拆分的过程也可以看出，既然X(z)的分母乘进了Y(z)里，那么拆分的时候必然又会分出来，所以最后的Y(z)的表达式一定包含了H(z)和X(z)两者的特征。
如果上面的H(z)的分子次数不大于分母（因果），对上面的式子进行IZT：

它是用下面这对ZT反推的：

y_n(n)来源于传递函数的极点，因此称为自由响应，与x(n)无关。每个p ^n称为系统的模态（其实就是对传递函数进行IZT之后得到的指数表达式，它反映了系统的特性）。
这样就把y(n)分成了强迫响应和自由响应，强迫响应是由输入决定的，自由响应是由系统决定的。如果x(n)是有界的，那么y_x(n)也是有界的，这是因为它们有相同的函数形式（Y_x(z)和X(z)有相同的极点）。所以，如果想让输出无界，那么必须让y_n(n)无界，也就是至少有一个kp^n是无界的，也就是至少有一个|p|>1。
反过来讲，系统BIBO稳定的条件是：传递函数的所有极点都位于z平面的单位圆内。如图：

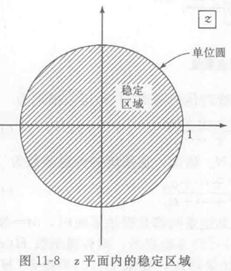
另一种说法：如果系统是稳定的，那么极点都在单位圆内，而h(n)是因果的，所以H(z)的收敛域是(R,∞)，要同时满足这两点，就要求R<1，即H(z)的收敛域包括单位圆。这是BIBO稳定的充要条件。

（3）可逆性
可逆系统的传递函数定义如下：

即

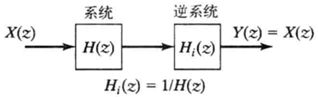
如果原系统的传递函数是这样的（M<=N）：

逆系统是这样的：

如果要让原系统和逆系统都是因果的，只有M=N
如果原系统稳定，则H的极点都在单位圆内，而逆系统稳定，则H的零点都在单位圆内。两个系统都稳定：H的零极点都在单位圆内。

4.3 从H(z)求系统的频率响应

系统的频率响应：对于不同频率的输入，得到的输出是什么样的。
采样函数的频谱是

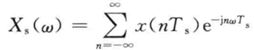
对比双边的ZT：

当

时，二者是相同的（x(nT_s)的T_s一般省略，和f(n)是一样的）。因此，可以说，采样函数的频谱可以投影到z平面的单位圆上。
为了求系统的频率响应，可以令

并在0<=Ω<=pi范围内计算传递函数，详细介绍在第12章。目前而言，下式在z平面上可以绘制单位圆的上半圆：

而

因此频率变量的范围0<=Ω<=pi是香农采样定理所允许的整个频率范围。
系统的频率响应表示为

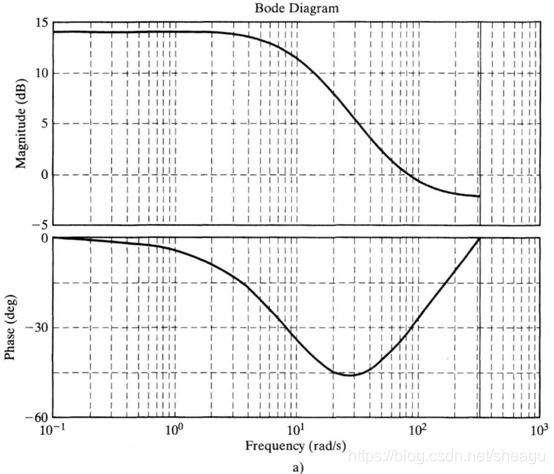
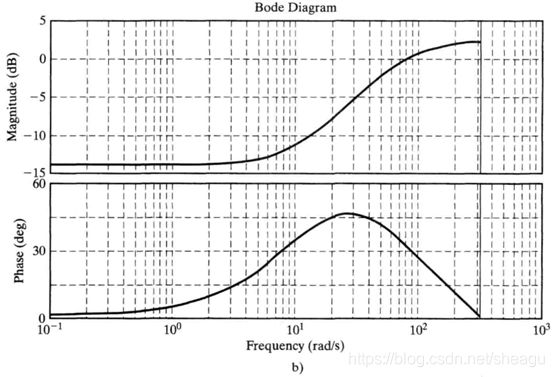
（1）一个例子

T是采样周期。逆系统是


图a是原系统的bode图，图b是逆系统的。从图a可以看出，系统在低频有一个不变的增益，高频则衰减，因此，原系统是一个低通系统。而逆系统是高频系统。
对于指定点的频率响应，这么算：


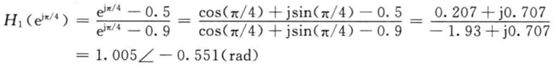
即

在图上也可以读出。

5 双边ZT

5.1 关于收敛域

双边ZT和IZT：


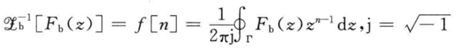
和单边的不同，双边的IZT需要知道收敛域才行。
对于右边信号，它的双边ZT和IZT可以直接用单边的公式，只需要注明收敛域（查表）。比如

收敛域是根据ZT的定义根据级数存在求的。

计算

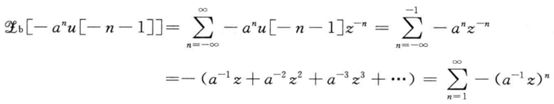
其中u(-n-1)在n>=0时为0，和u(n)互补。
因为

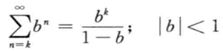
令b=a^(-1)z，k=1，得到：

收敛域也可以表示为|z|<|a|。对比一下：

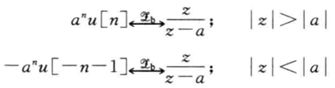
所以，如果不知道收敛域，那么根据z/(z-a)是不能确定IZT的。
（1）一个例子


考虑它们的差


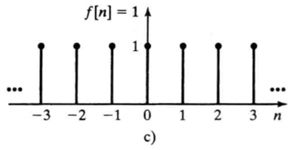
但是

因为右边的两个ZT不存在公共的收敛域，也就是说，对于ZT_b(1)而言，没有收敛的z存在，所以f(n)=1的ZT不存在。

5.2 关于函数和双边ZT的一些定义

（1）右边信号
f(n)=0, n （2）左边信号
f(n)=0, n>n_0
（3）双边信号
既不是右边，也不是左边，也就是不存在某个绝对值，使得|n|超过它之后f(n)=0。
（4）时限信号
既是左边，也是右边，可以看成是窗口截出来的。

5.3 双边ZT

对于一个函数，可以分解为两个信号：

f+是右边信号，f-是左边信号。如果双边ZT存在，那么可以表示为：


（1）指数序列的双边ZT
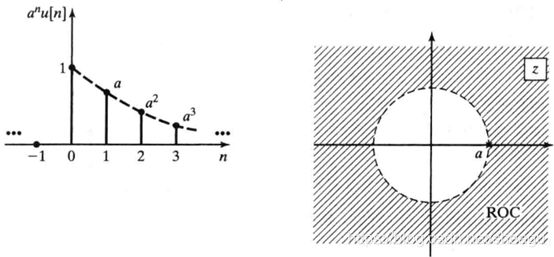
f(n)=a^|n|，如图

把f(n)表示为

分别进行ZT：


因此

只有在|a|<1的时候，这个变换才存在。

5.4 收敛域的进一步讨论

（1）f(n)只在n=0和1时非零
f(n)是一个时限信号。

这个相函数除了z=0外处处存在，因此收敛域是除原点外的整个z平面。
（2）f(n) 只在n=0和-1时非零

这个相函数在有界的z平面上处处存在，因此收敛域是除了无穷远处之外的整个z平面。
（3）f(n)是任一时限信号
一般来说，F_b(z)只能在原点和无穷点有极点。即，一个有限序列的双边ZT在有界的z平面上处处存在，原点可能除外。
（4）双边ZT的收敛域形式
右边信号：中心圆的外部
左边信号：中心圆的内部（原点可能除外）
双边信号：中心圆环
时限信号：整个有界的z平面（原点可能除外）
注意：收敛域都是开集，边界上常常有极点。

5.5 双边IZT

如何求双边IZT？
先拆开：

F+的极点在收敛域内侧，F-的极点在收敛域外侧，由此判断收敛域，得到F。
对于


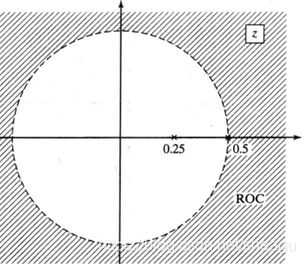
极点在收敛域内侧，f(n)是右边信号，因此

对于


收敛域在外侧，是左边信号

对于


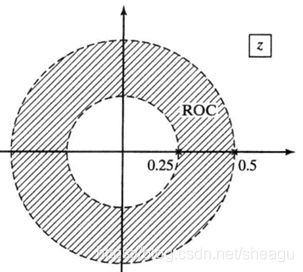
收敛域是圆环，z/(z-0.25)是右边的，z/(z-0.5)是左边的

参考文献

[1]Charles L.Phillips,John M.Parr,Eve A.Riskin(2014).信号、系统和变换(陈从颜等).北京:机械工业出版社(2015.1).