算法刷题笔记

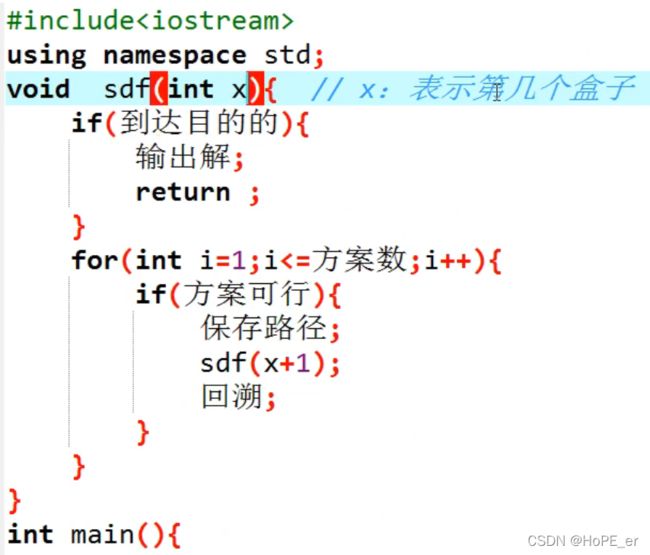
回溯问题

模板如下：

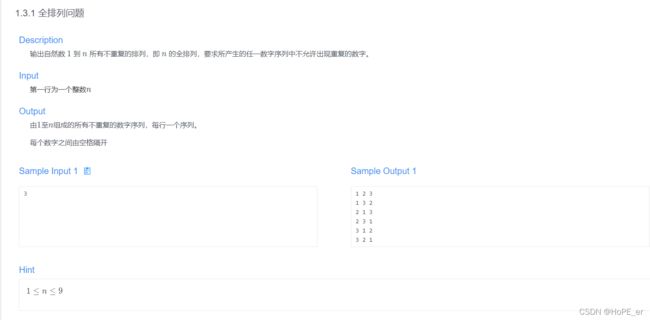
全排列问题

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        int len=nums.length;
        List<List<Integer>> res = new ArrayList<>();
        if(len==0) return res;
        boolean[] used = new boolean[len];
        List<Integer> path = new ArrayList<>();
        dfs(0,nums,len,used,path,res);
        return res;
    }
    public void dfs(int height,int[] nums,int len,boolean[] used,List<Integer> path,List<List<Integer>> res){
        if(height==len){
            res.add(new ArrayList<>(path));  //特别注意此处是new ArrayList<>(path)，这是因为java中指针问题
            return;
        }
        for(int i=0;i<len;i++){
            if(!used[i]){
                path.add(nums[i]);
                used[i]=true;
                dfs(height+1,nums,len,used,path,res);
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}

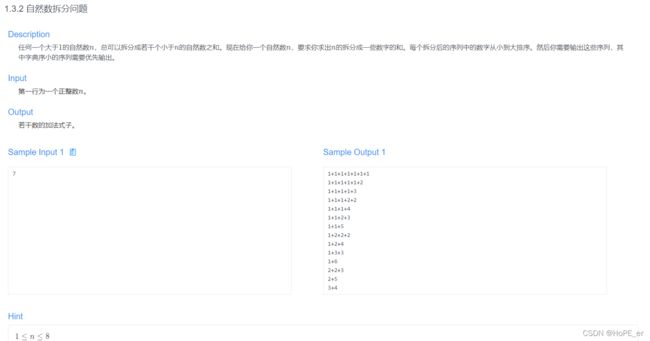
自然数拆分问题

此题b站教学视频

public class Test {
    @org.junit.Test
    public void test(){
        Scanner scanner = new Scanner(System.in);
        int sc = scanner.nextInt();
        int[] box=new int[200];
        sdf(1,sc,box);
    }
    //由于此处盒子的长度是会变的，不能用盒子长度判断结束条件，因此需要另寻条件变量
    void sdf(int x,int y,int[] box){  //此时x为盒子指针，y控制条件
        if(y==0 && x>2){
            for(int i=1;i<x;i++){
                System.out.println(box[i]+"+");
            }
            System.out.println(box[x]);
            return;
        }
        for(int i=1;i<=y;i++){
            if(i>=box[x-1]){
                box[x]=i;
                y-=box[x];
                sdf(x+1,y,box);
                box[x]=0;
                y+=box[x];
            }
        }
    }
}

动态规划

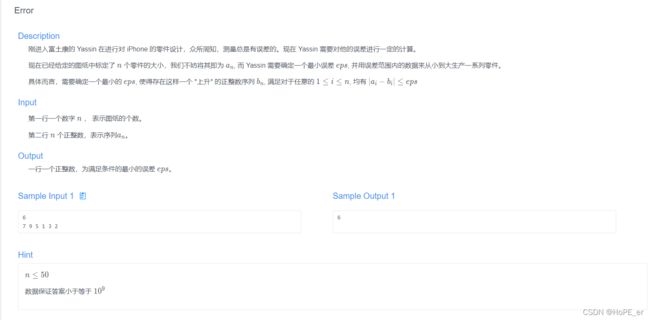
最长上升子序列

b站
问题描述：

思路：设置动态数组dp[i]，表示第i个数最长上升子序列的长度。那么再搞一个变量j，j从0–i之间遍历，如果nums[i]>nums[j],那么dp[i] = Math.max(dp[i], dp[j] + 1)。
对于1，4，5，3，6。dp[0] =1,dp[1]=2,dp[2]=3,dp[3]=2,再求dp[4]时就体现到了使用Math.max的原因了。

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

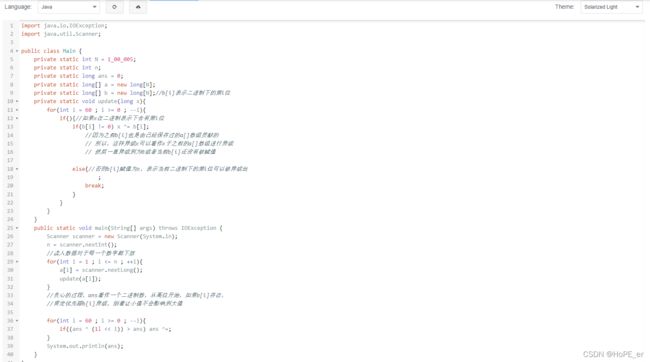
最长上升子序列（二分查找）

使用二分法求解最长上升子序列时需要构建一个辅助数组b[]用来记录上升子序列，用len表示上升子序列长度。（java使用ArrayList更方便）
代码如下：

执行过程：（注意） 此时求出的b只能记录上升子序列的长度，不能记录子序列。

最长公共子序列

B站讲解
问题描述：

启发： 对于双指针问题的状态转移方式，使用二维数组分别来记录i和j指到相应位置时
**dp[i][j]**来记录最终结果的中间状态变化。
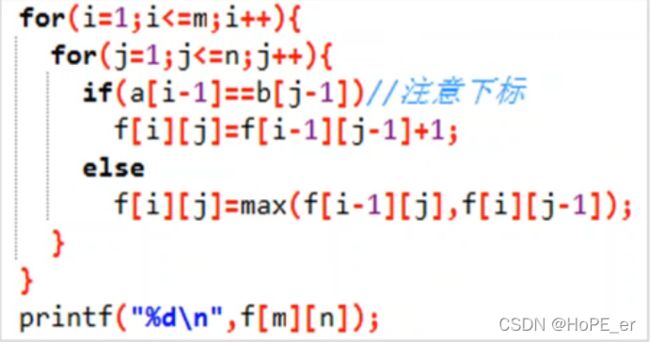
状态转移方程：

由此可得最长公共子序列长度：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp =new int[text1.length()+1][text2.length()+1];
        for(int i=1;i<=text1.length();i++){
            char c1 = text1.charAt(i-1);
            for(int j=1;j<=text2.length();j++){
                char c2 = text2.charAt(j-1);
                if(c1==c2){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}

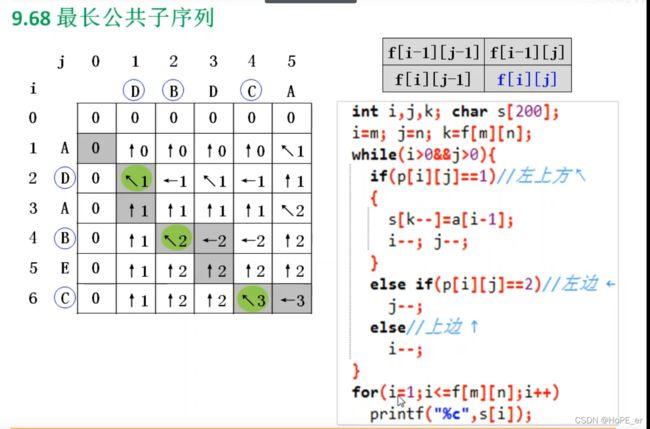
对于求解最长公共子序列问题（不只是求长度那么简单），需要一个中间变量**p[i][j]**来记录状态转移的过程。

p[i][j]记录了最长子序列成长过程（灰色部分）

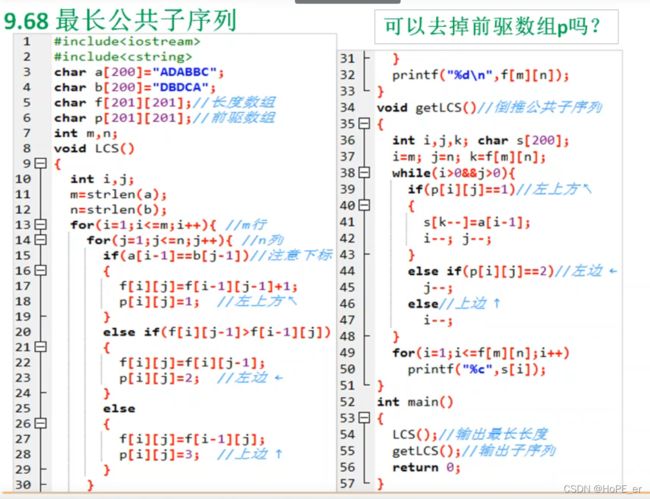
完整代码如下：

单调队列

滑动窗口

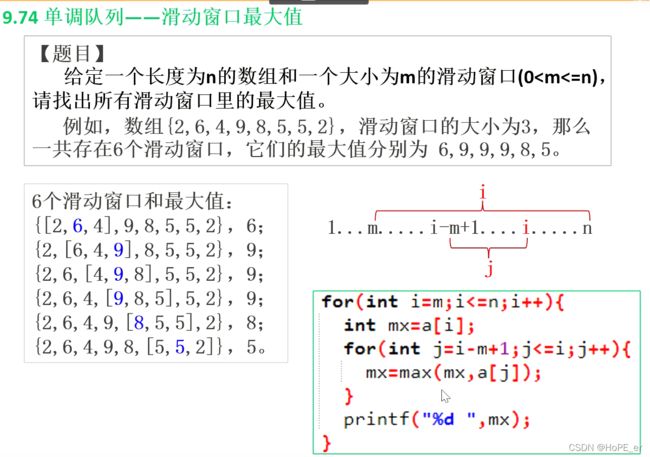
单调队列：

m=3大小的窗口，滑动取窗口内最大值过程模拟：


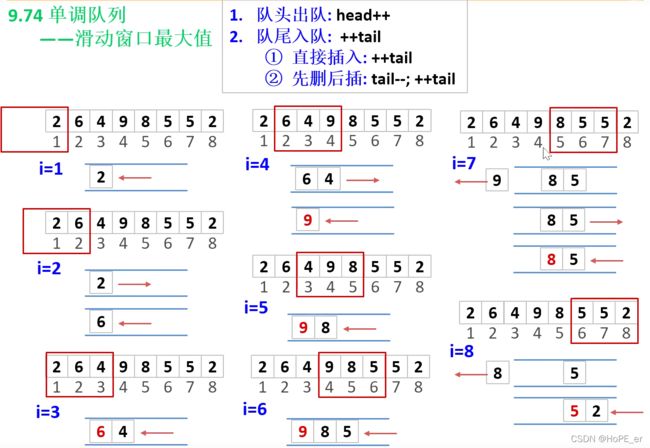
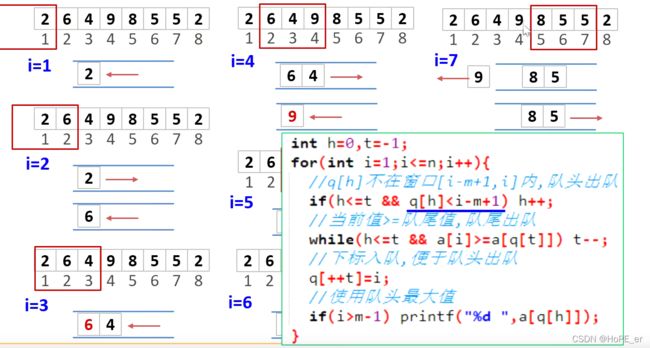
过程模拟

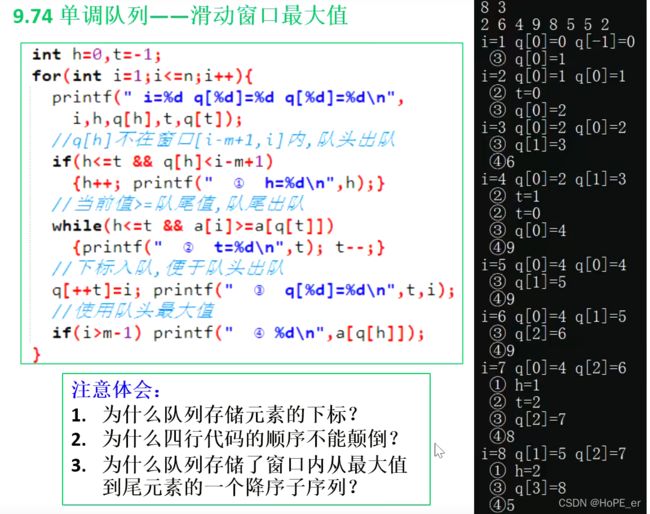
背包问题

b站讲解视频：背包问题

01背包

定义动态二维数组dp[i][j]。其中i表示可选物品的种类，j表示当前背包容量，dp[i][j] 的值表示当有i中可选为物品，背包容量为j时，所带来的最大价值（最优解）。
w[i]表示当前物品的重量
c[i]表示当前物品的价值

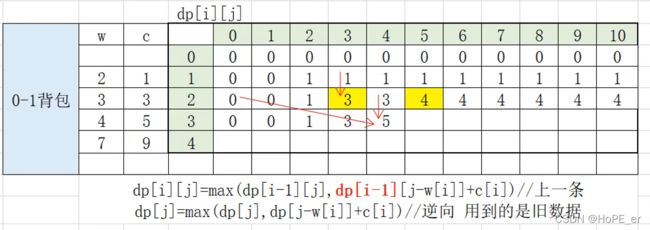
背包所能容纳的最大价值（dp[][]的最优解）求解过程：当来了一个新物品（i）时，随着背包容量不断增大（j++）,此时背包已经能够容纳新物品的重量，那么就要考虑要不要把该物品（第i个物品）放入背包。此时就是比较dp[i-1][j] 和 dp[i-1][j-w[i]]+c[i] 的大小。
dp[i-1][j] 表示：当前背包容量下，不选择第i个物品所带来的价值。
dp[i-1][j-w[i]]+c[i] 表示选择第i个物品所带来的价值。

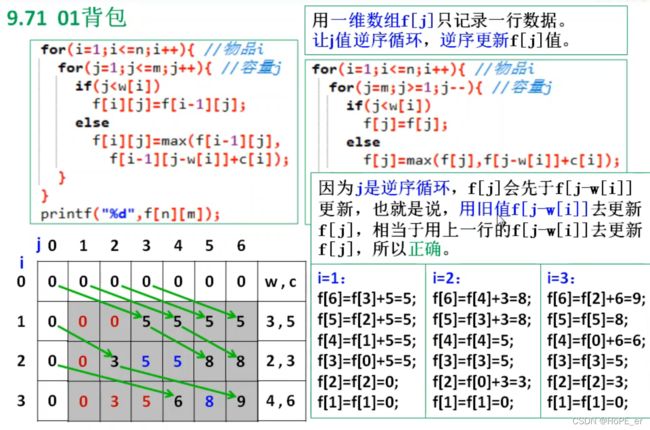
完全背包

完全背包问题和01背包的区别：完全背包中物品的数量是无限的，而01背包中物品的数量要么没有，要么一个。

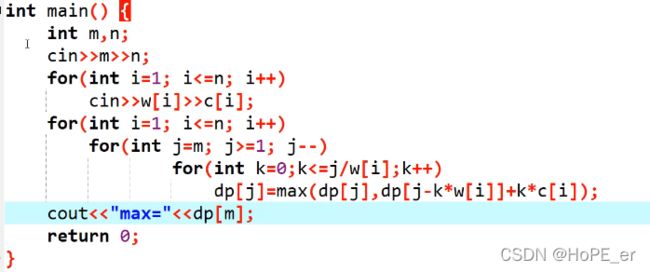
朴素的完全背包思想： 由于在完全背包中物品的数量是无限的，但是背包的容积V确是有限的，因此背包中可容纳的最多的某物品i的数量k=dp[j]/w[i] (dp[j]表示当前背包能容纳的重量，w[i]表示物品的重量)。
由此可在01背包的基础上加上一层循环即可：

由于完全背包可以放入多个同种物品，在二维dp状态下与01背包状态转移是有区别的：


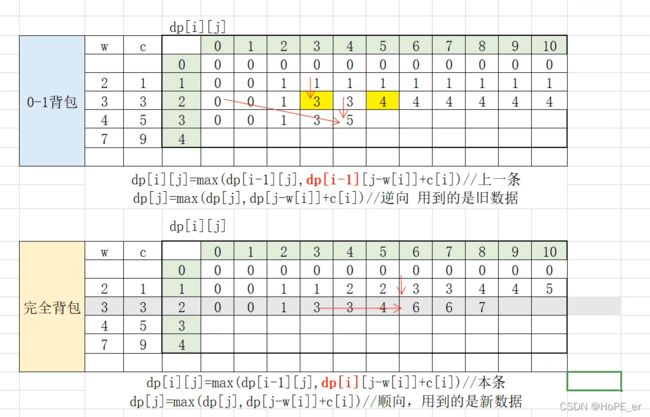
二维数组实现完全背包：

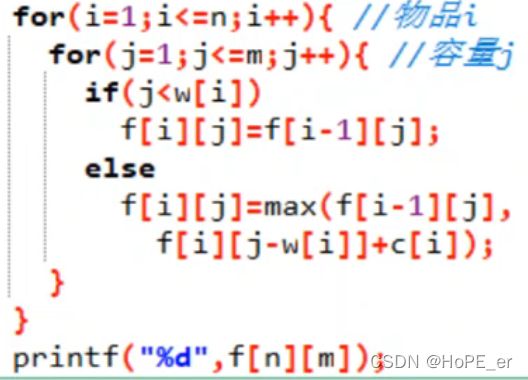
一维数组实现01背包和完全背包的差别：

多重背包

问题描述：与01背包不同的是，01背包只能取一件或零件，多重背包在取物品时可以取0.1.2…s件。
朴素算法：在朴素算法中，可以多加一个for循环，把多重背包问题转化为01背包问题：

朴素算法弊端：当k过大时容易超时，因此需要改进。

二进制优化方法：

混合背包

混合背包就是把01背包、完全背包、多重背包混合到一起。
问题描述：
处理思想：分类处理

把01背包和多重背包换做一类，将完全背包换成一类：

分别处理完全背包和01背包：

其他

字符串数组排序

对字符串数组进行从小到大排序，如果相等，则把字典顺序小的排后边。

字典树

实现 leetcode208
应用 leetcode720

Lambda表达式

Java8 Lambda表达式详解手册及实例

三目运算符

三目运算符踩坑

StringBuffer与StringBuilder

由于 StringBuilder 相较于 StringBuffer 有速度优势，所以多数情况下建议使用 StringBuilder 类。然而在应用程序要求线程安全的情况下，则必须使用 StringBuffer 类。
String、StringBuffer与StringBuilder

二分法

使用 int mid = l + (r - l) / 2 防止溢出
为什么mid这么计算

大数求余

答案对1e9+7（1000000007）取模原因
参考文章
大数求余原因：大数越界
大数越界：随着n增大，f(n)会超过Int32甚至Int64的取值范围，导致最终的返回值错误。
当一个问题只对答案的正确性有要求，而不在乎答案的数值，可能会需要将取值很大的数通过求余变小。
求余运算规则：
a mod b表示a除以b的余数。有下面的公式：
(a + b) % p = (a%p + b%p) %p
(a - b) % p = ((a%p - b%p) + p) %p
(a * b) % p = (a%p)*(b%p) %p
以防x，y本身就超出int32范围，可以创建一个long型变量tmp保存临时结果。

二维矩阵的常见转换技巧

两个技巧
leetcode661

位运算

位运算