线性代数的本质——动画+描述（向量、矩阵、线性变换和矩阵乘法）

线性代数的本质——动画+描述（向量、矩阵、线性变换和矩阵乘法）

---

源视频：

• 线性代数的本质 - 系列合集

---

一、向量和矩阵

1.向量的本质

在线性代数中，我们约定使用下述方式来描述向量——2×1的矩阵，在计算机中称为一维数组：


在二维空间中，两个向量的相加，即两个1×2的矩阵直接相加，符合了矩阵相加的定义

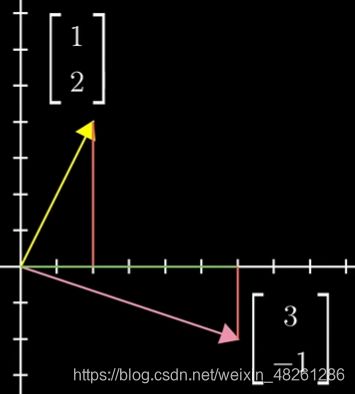
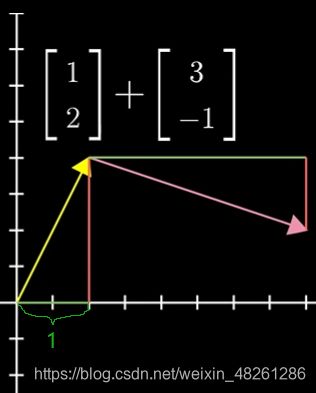
2.线性组合、张成的空间与基

在二维平面中，有两个十分重要的向量：i——i帽，x轴的单位向量；j——j帽，y轴的单位向量，二维平面中的所有点，都可以是 ai+bj 组成的二元方程来描述，它们是二维平面坐标系的基

一组基的方向是确定的，通过基的组合来定义的向量组合，那么这组向量可以通过向量的缩放——即模长发生变化来描述这组向量所指的位置——即 ai 和 bj 的线性组合构成 ai+bj

实际上，除了 i帽 和 j帽 外，我们完全可以指定另外任意一组基，如下图所示：下图中 v 和 w 的线性组合是基于除 i帽 和 j帽 外的另外一组基组成的

我们发现，线性组合通过向量的缩放（注：方向不变），我们可以得到二维平面上的所有点/所有向量，因此，当我们想要使用数字来描述向量时，我们都离不开坐标系的基，此时我们称这组基为一组线性组合

• 定义：对于所有可以表示为给定向量线性组合的向量的集合，称为给定向量张成的空间

因此，上述v 和 w 的线性组合所张成的空间是一个平面

此时，如果我们在 v 和 w 的线性组合的基础上再在三维空间上增加一个 u 向量，当我们对 u 向量进行缩放时，它能够将 v 和 w 所张成的平面延 u 的方向来回移动，从而扫过整个三维空间，这样，我们通过 v 、w 和 u 的线性组合就可以得到三维空间上的所有点/所有向量，这就是 u 向量对空间张成的贡献

再观察下图，我们发现，在二维空间中，如果一组向量组合在同一条直线上时，那么它们所张成的空间则是一条直线，而无法向一个平面进行扩展，即有一个基向量是多余的，没有对空间的张成作出贡献

同理，如果我们在三维空间内，也可以得到类似的情况，当新增的 u 向量是定义在 v 和 w 所张成的平面上时，那么它们所张成的空间仍然只是一个平面，而无法向三维空间扩展，即有一个基向量是多余的，没有对空间的张成作出贡献

• 定义：如果你有多个向量，并且可以通过移除其中一个向量而不减小张成的空间，我们称它们是线性相关的
• 或者说：在一组向量中，有其中一个向量，它落在了其他向量所张成的空间中时，就称它们是线性相关的
• 另一方面，如果所有向量都给张成的空间增添了新的维度，即所有向量都对空间的张成作出了贡献，就称它们是线性无关的

3.矩阵与线性变换（重点）

线性变换：简单理解来说，变换其实就是函数的另一种说法，即它接受一个输入，同时输出对应的结果。

线性变换一词实则是在暗示一种以特点的方式来可视化这一 输入-输出 的关系，那怎么用几何的手段描述这一过程呢？

在二维空间中，我们将用一个输入向量转换到输出向量的位置来理解线性变换

首先我们先将二维空间想象成一张无限网格：

这张二维空间网格是由无数的 点/向量 构成的，在二维空间发生变换时，我们可以想象成是二维网格上所有的点同时作变换

同时，为了更好地体会整个空间形状上的改变，我们在对无限网格上的所有点同时做变换的同时，在背景中保留原始网格的副本，以便追踪终点与起点的相对关系

二维空间的变换可以十分复杂，但幸运的是，线性代数限制在一种特殊类型的变换上——线性变换，在无限网格发生变化时，如果它具备以下两条性质，我们就称这种变换是线性的：

• 无限网格上的所有无限直线在变换后仍然保持为直线，不能有所弯曲
• 保持网格线的平行且等距分布
• 无限网格的原点必须保持固定，不能移动

（如：无限网格原点旋转就是线性变换，或上一动画演示的也是线性变换）

下图中，原变量为： v = -1i+2j，在运用某一线性变换后，我们发现变换后的向量 v 的位置，是变换后的 i帽 的 -1倍 与 变换后的 j帽 的 2倍 之和，即式 v = -1i+2j 仍然成立

经过下图中简单的运算，我们可以计算出向量 v 在经过刚才的线性变换之后，落在了原网格的 (5, 2) 上；其实由图即知，向量 v 确实落在了原网格的 (5, 2) 坐标上

实际上，我们发现只要记录了变换后的 i帽 和 j帽 的坐标，我们就可以推断出任意向量在变换后的位置，而不必观察变换本身是什么样的

这里给出我们在通过上次的线性变换之后，坐标所发生的变化，即我们只需知道：

• 变换后的 i帽 的坐标
• 变换后的 j帽 的坐标
• 任一 点/向量 的坐标

我们就可以求出某个 点/向量(x, y) 在发生某一线性变换后的坐标：(1x+3y, -2x+0y)

• 这就是说，一个二维线性变换仅由四个数字完全确定——“变换后的 i帽 的坐标” 和 “变换后的 j帽 的坐标”

• 通常我们会将这些坐标包装在一个 2×2 的格子里，称它为 2×2 矩阵

• 实际上它们就是两个特殊的向量：“变换后的 i帽 的坐标” 和 “变换后的 j帽 的坐标”

如果你有一个描述线性变换的 2×2矩阵，以及一个给定向量，你想要了解线性变换对这个向量的作用，你只需取出向量的坐标，将它们分别与矩阵的特点列相乘，然后将结果相加即可

于是，对于一般线性变换——(a, c) 看作是变换后的 i帽，(b, d) 看作是变换后的 j帽，研究该线性变换作用于向量 (x, y)


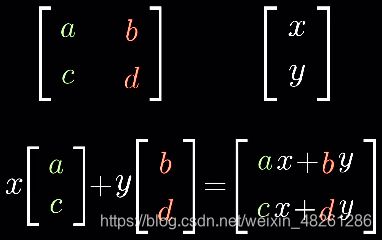
这就是线性变换对空间中 点/向量 的影响：

线性变换——旋转：

• 这种变换会将无限网格进行旋转变换

线性变换——错切：

• 这种变换会将无限网格的基轴线进行倾斜变换

线性变换——列线性相关：

• 列线性相关的线性变换会把二维空间拍扁成一条直线

例：想象出下图的线性变换

4.矩阵乘法

实际上，二维平面有时候需要进行多次线性变换（如图：先旋转，后错切）：

（1） 从数值的角度上看，某一向量 (x, y) 经过这两轮线性变换后的结果，可以是先乘以旋转矩阵，后乘以错切矩阵的结果——即代表发生了两次线性变换

（2） 实际上，我们还可以先将两次线性变换的矩阵合成为一个新的复合矩阵，再对向量 (x, y) 进行变换

复合的顺序和函数的 f(g(x)) 是一致的，我们应该先看右端的矩阵再看左端的矩阵——先经过旋转变换，后经过错切变换

• 实际上，（1）（2）两者的结果是一致的

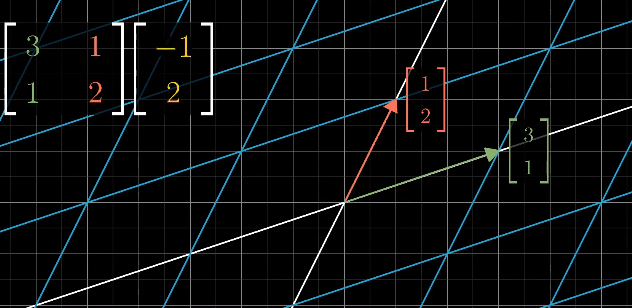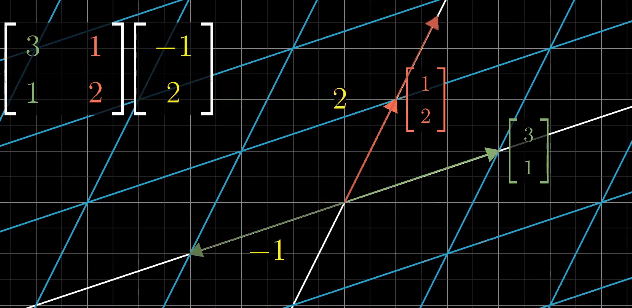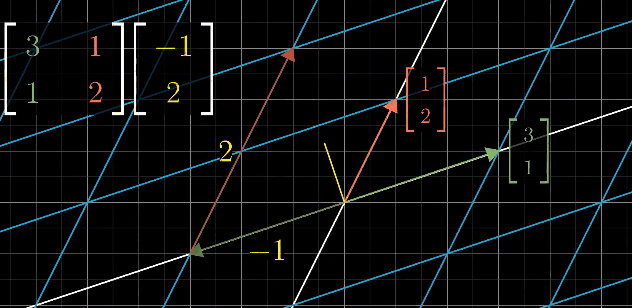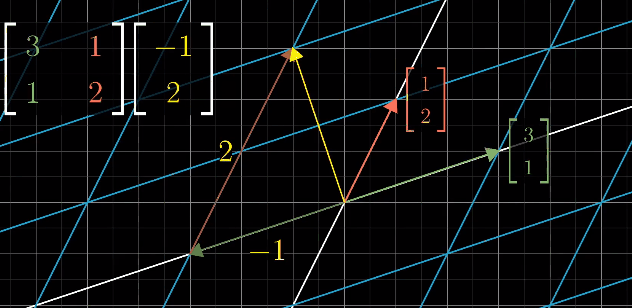
例如：对于 M2 × M1

我们可以把 经过 M1 矩阵变换后的基 i(1, 1) 和 j(-2, 0) 分别看作两个向量，并分别计算它们在 M2矩阵变换 下发生的变化：

• 把 M1 变换后的 i(1, 1) 视为一个向量
  
• 把 M2 变换后的 j(-2, 0) 视为一个向量
  
  

注：这种方法具有普适性，但是我们不能让 M1 和 M2 的反过来计算——即不能把M2视为坐标，因为我们是先进行 M1 变换，后进行 M2 变换的，这是因为 M1×M2≠M2×M1，这个就像函数的复合一样 f(g(x))≠g(f(x))，因为线性变换的先后顺序会影响到变换后的结果

因此，这就是矩阵相乘的几何意义

另外，对于矩阵的乘法结合律 (AB)C=A(BC)，如果仅仅从数学公式上的范畴来进行证明，这个过程是十分平凡的，你无法得到任何启发；但通过几何方式的线性变换证明，就会有所理解：

A(BC)：它的本质是C的坐标先经过B矩阵变换，再经过A矩阵变换

(AB)C：它的本质是AB矩阵变换的结果组成一个新的复合矩阵，再让C矩阵经过复合矩阵的变换

很显然，由于它们的变换顺序的是一致的，因此它们得到的结果也是一致的

二、待更新…

1.待更新…