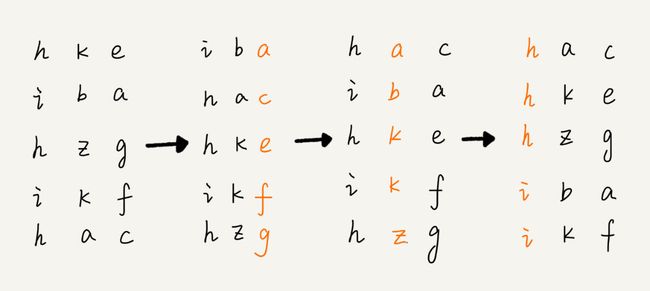【数据结构与算法-基础篇】
数据结构与算法
前言
本文只是学习极客时间 王争老师的《数据结构与算法》付费课程的学习笔记与心得,对《数据结构与算法》这门课有兴趣的同志可以通过以下链接购买专栏: https://time.geekbang.org/column/intro/100017301
附一张数据结构合算法知识地图:
一.复杂度分析
1.什么是复杂度分析?
1.复杂度描述的是算法执行时间(或占用空间)与数据规模的增长关系
2.时间复杂度:
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
3.空间复杂度:
空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
2.如何进行复杂度分析?
1.大O表示法
1)来源
算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。
2)特点
以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响,所以在做时间复杂度分析时忽略这些项。
2.复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
3.复杂度量级
多项式阶:
随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n2)(平方阶)、O(n3)(立方阶)
非多项式阶:
随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,O(2^n)(指数阶)、O(n!)(阶乘阶)

4.如何掌握好复杂度分析方法?
1. 只关注循环执行次数最多的一段代码
2. 加法法则:总复杂度等于量级最大的那段代码的复杂度,假设 T1(n) = O(n),T2(n) = O(n^2),则 T1(n) +T2(n) = O(n^2)。
3.乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积,假设 T1(n) = O(n),T2(n) = O(n^2),则 T1(n) * T2(n) = O(n^3)
4.忽略低阶,系数,常量
5.复杂度分析的4个概念
1.最坏情况时间复杂度:代码在最坏情况下执行的时间复杂度。
2.最好情况时间复杂度:代码在最理想坏情况下执行的时间复杂度。
3.平均时间复杂度:用代码在所有情况下执行的次数的加权平均值表示。
4.均摊时间复杂度:在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。
6.如何分析平均、均摊时间复杂度?
1.平均时间复杂度
代码在不同情况下复杂度出现量级差别,则用代码所有可能情况下执行次数的加权平均值表示。
2.均摊时间复杂度
两个条件满足时使用:1)代码在绝大多数情况下是低级别复杂度,只有极少数情况是高级别复杂度;2)低级别和高级别复杂度出现具有时序规律。均摊结果一般都等于低级别复杂度。
二. 基础数据结构(线性数据结构)
1.递归
1.问题递归分析需满足条件?
- 可以将一个问题的解法分成若干个子问题的解法
- 父子问题解法相同,只是数据量不同
- 有递归终止条件
2.递归代码要素:
- 递推公式
- 终止条件
3.问题?
question one: 在电影院如何确定在自己第几排?(假设忘记在第几排,且看不清电影票详细信息)
我们可以问前面的哥们他在第几排,我们将排数+1就好了;前面的人也不知道,再问前面的人排数+1,直到第一排;
思路:分解成一个个子问题就是 前排是第几排 ,递推公式就是f(n) = f(n-1) + 1,终止条件就是找到第1排f(1) = 1;
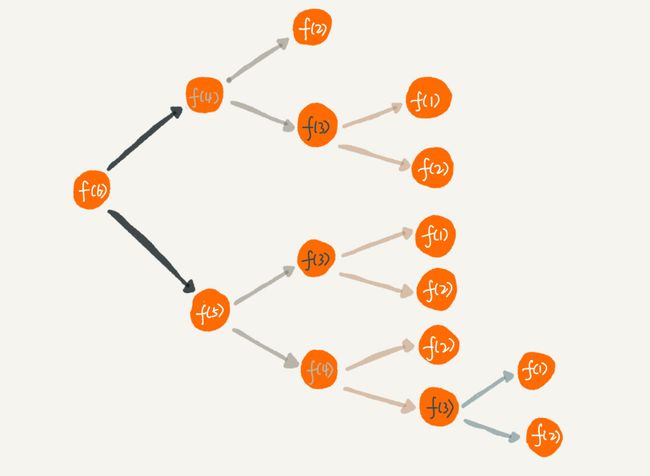
question two: 假设有n个台阶,每次只能走1阶或2阶,那么有多少种走法?
思路:假设我们第一次走了1步,那么我们只需要算接下来n-1台阶的走法;我们如果第一次走了2步,只需要算剩下n-2个台阶的走法;
所以我们只要将问题分成第一次走1阶多少种走法,第一次走2阶多少种走法两个子问题,他们结果相加就是父问题的结果;所以递归公式为: f(n) = f(n-1) + f(n-2);
当n=1时,f(1)=1;当n=2时,f(2)=2; 当n=3时,f(3)=f(2)+f(1);
所以终止条件为: f(1) = 1; f(2) = 2;
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}
4.递归优缺点
优点:
代码整洁清晰,简洁高效
缺点(注意):
堆栈溢出
重复计算
耗时(频繁调用函数)
空间复杂度高(频繁调用函数)
5. 堆栈溢出 和 重复计算 解决方案
1.堆栈溢出
减少递归深度,例如 电影票的例子
// 全局变量,表示递归的深度。
int depth = 0;
int f(int n) {
++depth;
if (depth > 1000) throw exception;
if (n == 1) return 1;
return f(n-1) + 1;
}
2.重复计算
为了避免重复计算,我们可以通过一个数据结构(比如散列表)来保存已经求解过的 f(k)。当递归调用到 f(k) 时,先看下是否已经求解过了。如果是,则直接从散列表中取值返回,不需要重复计算,这样就能避免刚讲的问题了。
public int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
// hasSolvedList可以理解成一个Map,key是n,value是f(n)
if (hasSolvedList.containsKey(n)) {
return hasSolvedList.get(n);
}
int ret = f(n-1) + f(n-2);
hasSolvedList.put(n, ret);
return ret;
}
6.递归代码转换为非递归代码
所有递归代码都可以转换为非递归代码
f(x) =f(x-1)+1
int f(int n) {
int ret = 1;
for (int i = 2; i <= n; ++i) {
ret = ret + 1;
}
return ret;
}
f(x) =f(x-1)+f(x-2)
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
int ret = 0;
int pre = 2;
int prepre = 1;
for (int i = 3; i <= n; ++i) {
ret = pre + prepre;
prepre = pre;
pre = ret;
}
return ret;
}
7.检测"环"
推荐注册返佣金的这个功能我想你应该不陌生吧?现在很多 App 都有这个功能。这个功能中,用户 A 推荐用户 B 来注册,用户 B 又推荐了用户 C 来注册。我们可以说,用户 C 的“最终推荐人”为用户 A,用户 B 的“最终推荐人”也为用户 A,而用户 A 没有“最终推荐人”。
一般来说,我们会通过数据库来记录这种推荐关系。在数据库表中,我们可以记录两行数据,其中 actor_id 表示用户 id,referrer_id 表示推荐人 id。基于这个背景,我的问题是,给定一个用户 ID,如何查找这个用户的“最终推荐人”?
long findRootReferrerId(long actorId) {
Long referrerId = select referrer_id from [table] where actor_id = actorId;
if (referrerId == null) return actorId;
return findRootReferrerId(referrerId);
}
问题:
如果数据库里存在脏数据,我们还需要处理由此产生的无限递归问题。比如 demo 环境下数据库中,测试工程师为了方便测试,会人为地插入一些数据,就会出现脏数据。如果 A 的推荐人是 B,B 的推荐人是 C,C 的推荐人是 A,这样就会发生死循,我们怎样检测"环"呢?
解决方案:
构建一个set集合或者散列表,每次获取到上层推荐人就看散列表有没有,有的话就出现“环”的问题;
快慢指针;
可以拿到A-B-C…的hash码,遍历时进行异或运算,靠异或值是否是0,如果出现"环"结构,那么异或值会变成0.(此种请框只能检测出 A-B-C-A类型,无法检测出A-B-C-B类型)
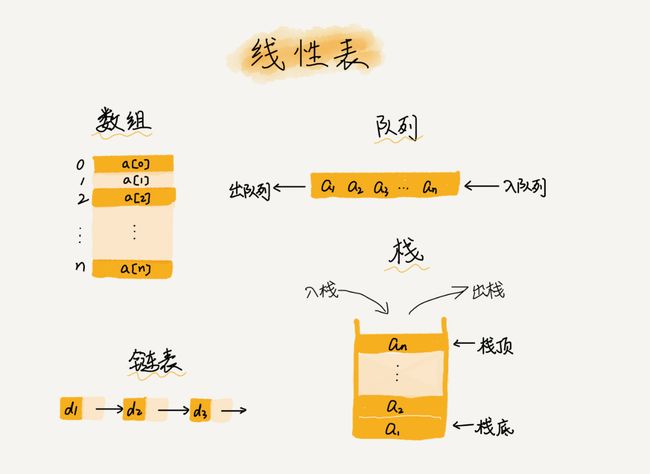
2.数组
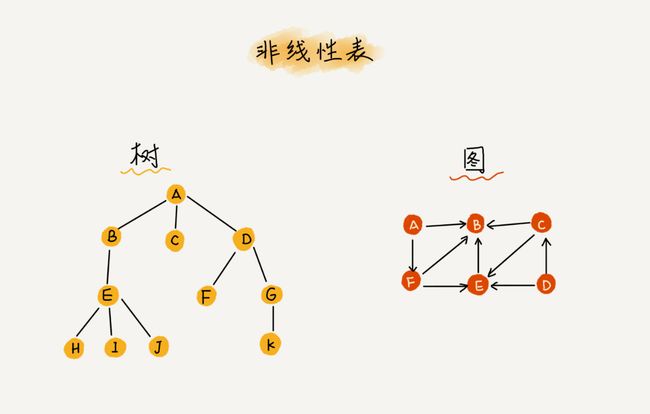
1.线性与非线性数据结构
线性:顾名思义,各个数据节点在一条线上,可以对其首尾进行操作,每个节点下面有不超过两个子节点;
例如:数组,链表,队列,栈
非线性:结构相对复杂,每个节点下面可以有多个子节点;例如:树,位图,堆
2.数组的特点
- 线性结构
- 连续的空间地址,且只能存储相同类型
- 不支持扩容
数组是一种存储相同类型数据的有一组连续空间地址的线性数据结构。
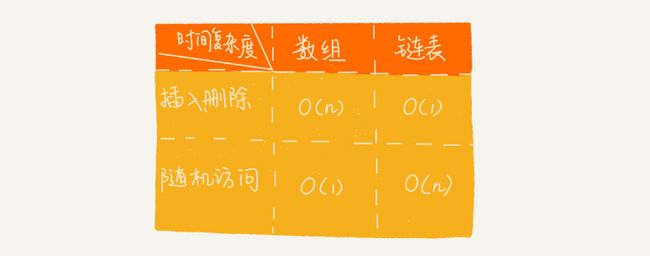
数组随机访问时间复杂度为O(1),查找的时间复杂度为O(n)
3.容器与数组
数组插入,删除时需要大量数据搬移,操作复杂且效率比较低;
操作复杂的运算可以用容器代替;
ArrayList 可以自动扩容为原来空间的1.5倍;
1.Java ArrayList 无法存储基本类型,比如 int、long,需要封装为 Integer、Long 类,而 Autoboxing、Unboxing 则有一定的性能消耗,所以如果特别关注性能,或者希望使用基本类型,就可以选用数组。
2.如果数据大小事先已知,并且对数据的操作非常简单,用不到 ArrayList 提供的大部分方法,也可以直接使用数组。
3.要表示多维数组时,用数组往往会更加直观。比如 Object[][] array;而用容器的话则需要这样定义:ArrayList > array。
4.为什么数组下标从0开始?
为什么数组下标从0开始?这要归功于其连续的空间地址,以及寻址公式;
k表示要寻找元素的下标,base_address 首地址,type_size每个元素所占空间大小
下表为0时:
a[k]_address = base_address + k * type_size
下表为1时:
a[k]_address = base_address + (k-1) * type_size
下标为1时,cpu要多做一次减运算,由于寻址操作非常底层,所以设计下标为更高效;
历史原因:C语言设计数组下标为0
5.数组插入删除优化小技巧
插入:
比如在a,b,c,d,e 五个元素的第三个位置(下标为2)插入元素x,那么我们可以先把c保存在数组末尾,在把x替换到原来的c位置,结果为a,b,x,d,e,c
删除:
假如删除a,b,c,d,e中的a,b那么后面的三个元素要经过两次数据搬移,效率低,那么我们能不能每次的删除只是记录数据已经被删除。当数组没有更多空间存储数据时,我们再触发执行一次真正的删除操作,这样就大大减少了删除操作导致的数据搬移。
3.链表
参考:
单链表工具类:https://www.cnblogs.com/zhou-test/p/10036832.html
单链表反转:http://c.biancheng.net/view/8105.html
1.链表分类
链表是线性数据结构,逻辑上连续,但在内存中不连续;
-
单链表由数据data区和next指针组成;
-
双链表由数据区data,pre指针合计next指针组成;
-
循环链表;
2.单链表与双链表
链表删除不外乎两种情况:
1.给定一个值,删除等于当前值的节点;
两者都要先遍历后删除,遍历的时间复杂度是O(n)
2.给指向某个节点的指针,删除当前节点
双链表删除的时间复杂度是O(1),而单链表还要遍历获取该指针的前驱结点pre,然后删除,所以时间复杂度是O(n)
3.链表VS数组性能
数组缺点
1)若申请内存空间很大,比如100M,但若内存空间没有100M的连续空间时,则会申请失败,尽管内存可用空间超过100M。
2)大小固定,若存储空间不足,需进行扩容,一旦扩容就要进行数据复制,而这时非常费时的。
链表缺点
1)内存空间消耗更大,因为需要额外的空间存储指针信息。
2)对链表进行频繁的插入和删除操作,会导致频繁的内存申请和释放,容易造成内存碎片,如果是Java语言,还可能会造成频繁的GC(自动垃圾回收器)操作。
如何选择?
数组简单易用,在实现上使用连续的内存空间,可以借助CPU的缓冲机制预读数组中的数据,所以访问效率更高,而链表在内存中并不是连续存储,所以对CPU缓存不友好,没办法预读。
如果代码对内存的使用非常苛刻,那数组就更适合。
4.练习
链表实现LRU缓存策略;
检测环;
两个有序链表合并;
单链表反转;
删除单链表倒数第K个元素;
链表头插,尾插;
求链表中间节点;
链表代码技巧:使用哨兵节点解决边界问题;
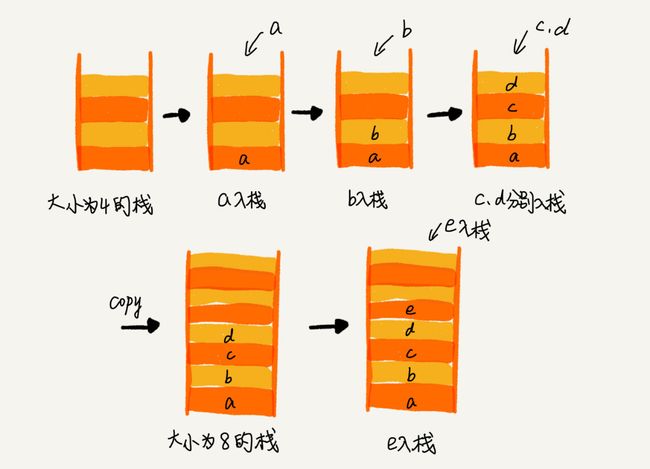
4.栈
1.特征及实现
先进后出;
// 基于数组实现的顺序栈
public class ArrayStack {
private String[] items; // 数组
private int count; // 栈中元素个数
private int n; //栈的大小
// 初始化数组,申请一个大小为n的数组空间
public ArrayStack(int n) {
this.items = new String[n];
this.n = n;
this.count = 0;
}
// 入栈操作
public boolean push(String item) {
// 数组空间不够了,直接返回false,入栈失败。
if (count == n) return false;
// 将item放到下标为count的位置,并且count加一
items[count] = item;
++count;
return true;
}
// 出栈操作
public String pop() {
// 栈为空,则直接返回null
if (count == 0) return null;
// 返回下标为count-1的数组元素,并且栈中元素个数count减一
String tmp = items[count-1];
--count;
return tmp;
}
}
2.案例
浏览器前翻后翻:
可以用两个栈存储,前翻a栈出栈数据进入b栈,后翻b栈数据出栈进入a栈,a栈栈顶就是我们当前页面
函数调用栈:
一行行压栈,遇到函数创建栈帧空间;
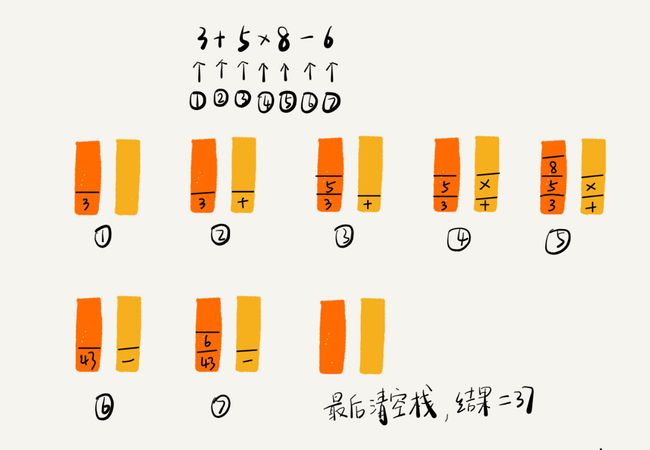
表达式运算符:
一个栈存数,一个栈存运算符,当前运算符优先级<=栈顶运算符,数据±*/
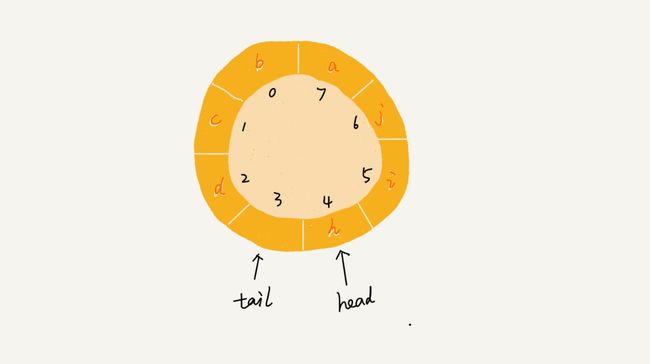
5.队列
1.队列知识点
先进先出
操作首尾两端
用数组实现的叫顺序队列(运用广泛),用链表实现的叫链式队列
2.循环数组队列代码
/*
* 数组实现循环顺序队列
* 队满条件:(tail+1)%length = head
* 队空条件: tail == head
* 循环队列会浪费一个元素空间
* */
public class CircleArrayQueue {
private String[] s;
private int length = 0;
private int head = 0;
private int tail = 0;
public CircleArrayQueue(String[] s, int length){
this.s = s;
this.length = length;
}
/*入队*/
public boolean enqueue(String str){
/*(tail+1)%length == head表示队满*/
if((tail+1)%length == head){
s[tail] = str;
tail = (tail+1)%length;
return true;
}
return false;
}
/*出队*/
public String dequeue(){
if(head == tail){
return null;
}
String res = s[head];
head = (head+1)%length;
return res;
}
}
3.阻塞队列和并发队列
阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说,就是在队列为空的时候,从队头取数据会被阻塞。因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后再返回。
基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列。
队列场景:对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。
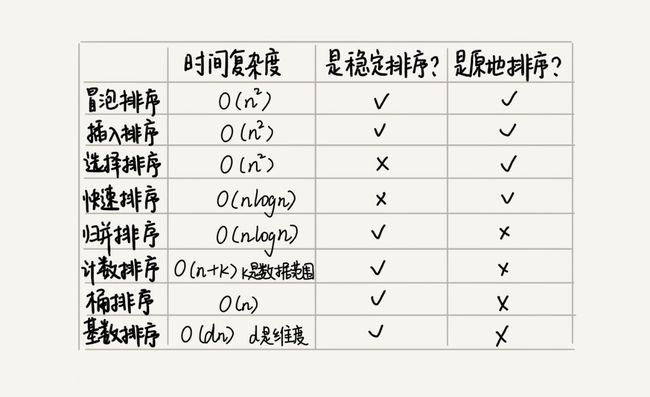
6.排序
概念
原地排序: 空间复杂度为O(1)的算法
稳定排序: 例如:3 2 2 1,排序后两个"2"的位置不会调换
1. O(n2)排序算法(冒泡,插入,选择排序)
1.1冒泡排序
原理:**冒泡排序只会操作相邻的两个数据。**每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
/*冒泡排序*/
public void bubbleSort(int[] a,int n){
if(n <=1 ) return;
boolean breakCondition;
for (int i = 0; i < n; i++) {
breakCondition = true;
for (int j = 0; j < n-1-i; j++) {
if(a[j]>a[j+1]){
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
breakCondition = false;
}
}
/*循环提前终止条件:没有元素交换*/
if(breakCondition) break;
}
}
1.2插入排序
原理:**将数组中的数据分为两个区间,已排序区间和未排序区间。**初始已排序区间只有一个元素,就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
/*插入排序*/
public void insertSort(int[] a,int n){
if(n <=1 ) return;
for (int i = 1; i < n; i++) {
int insertItem = a[i];
int j = i-1;
for (;j >=0; j--) {
if(insertItem<a[j]){
a[j+1] = a[j];
}else {
break;
}
}
a[j+1] = insertItem;
}
}
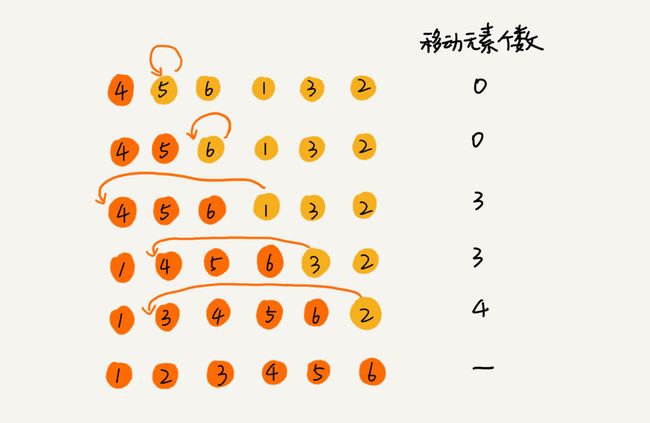
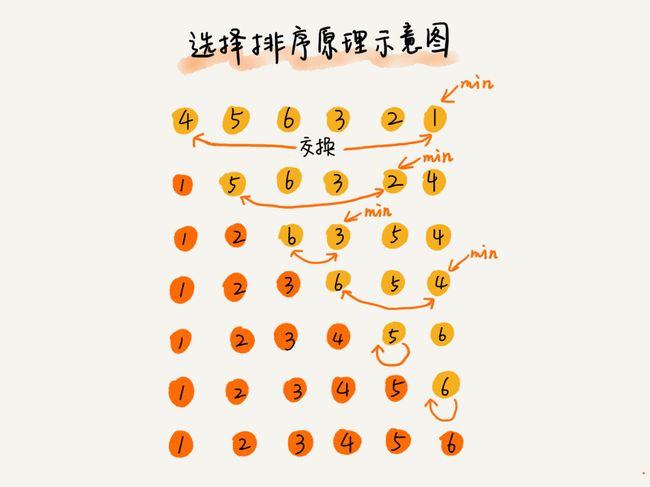
1.3 选择排序
原理:选择排序也分已排序区间和未排序区间,只是在未排序区间找到最小值,放入已排序区间的末尾;
/*选择排序*/
public void selectSort(int[] a,int n){
if(n<=1) return;
int minIndex;
int minValue;
for (int i = 0; i < n-1; i++) {
minIndex = i;
minValue = a[i];
for (int j = i+1; j < n; j++) {
if(a[j]<minValue){
minIndex = j;
minValue = a[j];
}
}
a[i] = minValue;
a[minIndex] = a[i];
}
}
1.4 为什么插入排序比冒泡排序更受欢迎?
从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要 3 个赋值操作,而插入排序只需要 1 个。
冒泡排序中数据的交换操作:
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
}
插入排序中数据的移动操作:
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
2. O(nlogn)排序算法(归并,快排排序)
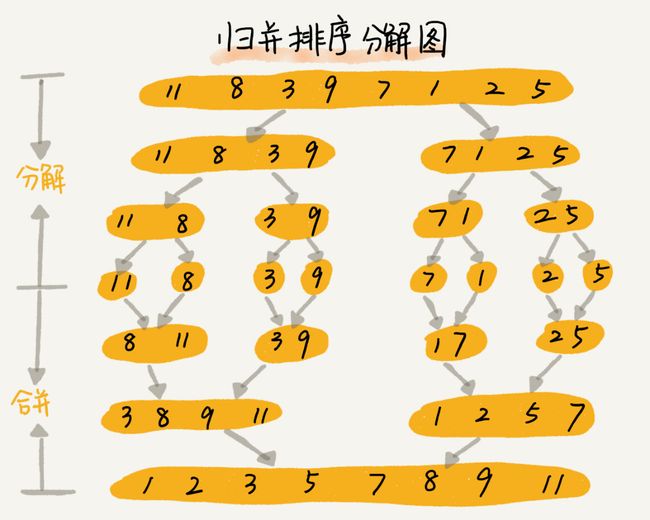
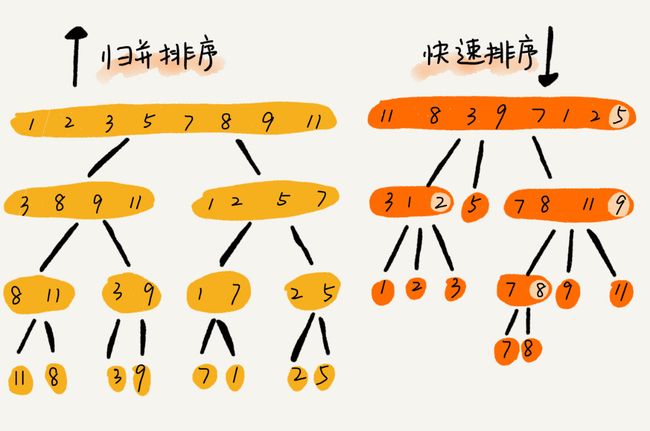
2.1 归并排序
原理:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
/*归并排序(分治思想)
* 排序原数组,等于将原数组拆分两个子数组,对两个子数组排序,然后将排序好的数组合并
*递推公式:merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
* 终止条件:p >= r 不用再继续分解
* 时间复杂度:O(nlogn)
* 空间复杂度:O(n)
* */
public void merge_sort(int[] a, int p,int r){
if(p>=r) return;
int q = (p+r)/2;
merge_sort(a,p,q);
merge_sort(a, q+1, r);
merge(a, p, q, r);
}
/*将两个区间的元素排序合并到创建的临时数组
* 再将排序好的临时数组放入数组a
* */
public void merge(int[] a,int p,int q,int r){
int s = q+1;
int[] tmp = new int[r-p+1];
int i = 0;
while(p<=q && s<=r){
if(a[p]<=a[s]){
a[i] = a[p];
p++;
}else{
a[i] = a[s];
s++;
}
i++;
}
int start = 0,end = 0;
if(p>q){
start = s;
end = r;
}
if(s>r){
start = p;
end = q;
}
while(start<=end){
a[i] = a[start];
start++;
i++;
}
for (int j = 0; j < tmp.length; j++) {
a[j+p] = tmp[j];
}
}
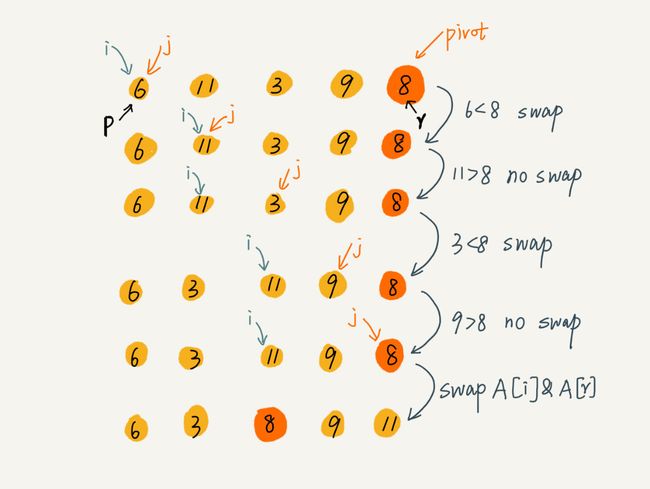
2.2 快排
原理:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。
/*
* 快排
* 选取最后一个元素为分区点,小于它的元素放左边,反之放右边
*递推公式 quick_sort(p,r) = quick_sort(p,pivot-1)+quick_sort(pivot+1,r)
* 终止条件 p>=r
* 时间复杂度O(nlogn),空间复杂度O(1)
* */
public void quickSort(int[] a,int p,int r){
if(p>=r) return;
int pivot = partition(a,p,r);
quickSort(a, p, pivot-1);
quickSort(a, pivot+1, r);
}
/*分区*/
public int partition(int[] a,int p,int r){
int pivot = r;
int pivotValue = a[r];
int i = p;
int j = p;
for (; j <= r-1; j++) {
if(a[j]<pivotValue){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
i++;
}
}
a[pivot] = a[i];
a[i] = pivotValue;
return i;
}
缺点:当数组是有序的,例如:1,2,3,4,5,6 快排时间复杂度退化为O(n2)
解决方式:
- 三点取中法(数据量大,需要多点取中):在区间的两端,中间位置取值,比较获取中间值,确定分区
- 随机法:随机取分区点
2.3 比较
归并排序自下而上,先解决子问题,再合并;快排自上而下 先分区,再解决子问题。
归并排序比较稳定 栈的深度是logn 非常小 所以相对快排堆栈溢出几率较小;
归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。
2.4 快排优化
1.选取合理的分区点
- 三点取中法(数据量大,需要多点取中):在区间的两端,中间位置取值,比较获取中间值,确定分区
- 随机法:随机取分区点
2.警惕递归深度
- 限制递归深度,一旦递归超过了设置的阈值就停止递归。
- 在堆上模拟实现一个函数调用栈,手动模拟递归压栈、出栈过程,这样就没有系统栈大小的限制。
2.5.Java的Arrays.sort使用的排序算法
1.若数组元素个数总数小于47,使用插入排序
2.若数据元素个数总数在47~286之间,使用快速排序。应该是使用的优化版本的三值取中的优化版本。
3.若大于286的个数,使用归并排序。
3. O(n)排序算法(桶,计数,基数排序)
3.1桶排序
原理:核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
场景:较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
对数据要求:
-
数据的范围有限,可被分配到多个桶中,数据量大
-
数据分布均匀,对于某个臃肿的桶(某个范围的数据量巨大),可以再次进行分桶
案例:10GB 的订单数据,希望按订单金额,但是内存有限,只有几百 MB,没办法一次性把 10GB 的数据都加载到内存中,我们怎么办?
- 首先扫描数据获取金额范围,加入范围是1-10w
- 我们每1000个数据区间分为一个桶,并排号
- 对于数据量大的范围再次分桶排号
- 依桶号把桶内数据放入内存,快排
- 排序数据追加写入文件
3.2 计数排序
计数排序是特殊的桶排序;
每个桶内的排序数据值相同;
原理:当要排序的 n 个数据,所处的范围并不大的时候,比如最大值是 k,我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的,省掉了桶内排序的时间。
场景:计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
案例:给几百万考生分数排序;根据年龄给数千万的人排序;
3.3 基数排序
假设我们有 10 万个手机号码,希望将这 10 万个手机号码从小到大排序,你有什么比较快速的排序方法呢?
刚刚这个问题里有这样的规律:假设要比较两个手机号码 a,b 的大小,如果在前面几位中,a 手机号码已经比 b 手机号码大了,那后面的几位就不用看了。
先按照最后一位来排序手机号码,然后,再按照倒数第二位重新排序,以此类推,最后按照第一位重新排序。经过 11 次排序之后,手机号码就都有序了。
手机号码稍微有点长,画图比较不容易看清楚,我用字符串排序的例子,画了一张基数排序的过程分解图,你可以看下。
注意,这里按照每位来排序的排序算法要是稳定的,否则这个实现思路就是不正确的。
根据每一位来排序,我们可以用刚讲过的桶排序或者计数排序,它们的时间复杂度可以做到 O(n)。
场景:基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系,如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到 O(n) 了。
4.案例
现在你有 10 个接口访问日志文件,每个日志文件大小约 300MB,每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件,合并为 1 个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB,你有什么好的解决思路,能“快速”地将这 10 个日志文件合并吗?
解决方案:
- 申请10个50M(需要根据实际情况)的数组,分别读入10个文件的50M数据
- 找到10个数组中最大值,比较得到他们的最小值pivot
- 在每个数组中二分查找小于pivot的临界点,在数组中标记
- 把小于pivot的数据放入临时数组,快排
- 删除小于pivot的数据,或者不做处理
- 继续从10个日志文件读取数据到数组,尽量读满50M
- 重复以上操作
7. 查找
1. 查找一个数组中的第K大元素
方法:使用快排分区的思想,把大于pivot的元素放左边,小于pivot的元素放右边;
如果pivot+1==k,那么a[pivot]就是我们要找的元素,如果pivot+1>k,那么我们在(p,pivot-1)区间寻找,
否则在(pivot+1,r)区间寻找;递归之后,a[k-1]就是我们要找的元素;
/*在数组中找出第K大元素*/
public int getK(int[] a,int k) throws Exception {
if(k<1 || k>a.length){
throw new Exception();
}
quickSearchK(a,0,a.length-1,k);
System.out.println(a[k-1]);
return a[k-1];
}
public void quickSearchK(int[] a,int p,int r,int k) {
if(p>=r) return;
int pivot = partition(a,p,r);
if(pivot+1 == k){
return;
}
if(pivot+1 > k){
r = pivot-1;
}else{
p = pivot+1;
}
quickSearchK(a,p,r,k);
}
/*分区,大于分区点的放在左边,小于的放在右边*/
public int partition(int[] a,int p,int r){
int pivot = r;
int pivotValue = a[r];
int i = p;
int j = p;
for (; j <= r-1; j++) {
if(a[j]>pivotValue){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
i++;
}
}
a[pivot] = a[i];
a[i] = pivotValue;
return i;
}
2.二分查找
1.原理
二分查找也叫折半查找,要求数组为有序数组,根据数组随机访问的特性,用数组下标low,high获取mid,如果a[mid]相同等于查找的定值value,return mid,小于则high=mid-1,否则low = mid+1,直到找到要查找的元素,或者区间被缩小为 0。
时间复杂度:O(logn)
k 的值就是总共缩小的次数,我们可以求得 k=log2n,所以时间复杂度就是 O(logn)。
2.求值的二分查找
注意点
1. 循环退出条件:low<=high
2. mid取值:mid=(low+high)/2 这种写法是有问题的。因为**如果 low 和 high 比较大的话,两者之和就有可能会溢出。**改进的方法是将 mid 的计算方式写成 **low+(high-low)/2**。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以 2 操作转化成位运算 **low+((high-low)>>1)。**
3. low 和 high 的更新:low=mid+1,high=mid-1
应用场景
1. 二分查找依赖数组下标的随机访问,所以必须是数组,且为**有序数组**;
2. **数据量不能太小**,例外:**数据之间的比较操作非常耗时,需要减少比较的次数**,推荐二分查找
3. 数据量不能过大,数组是**连续内存空间**
代码实现(递归和非递归)
/*二分查找*/
public int binarySearch(int[] a, int value){
int low = 0;
int high = a.length-1;
int mid = 0;
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] == value) return mid;
if(a[mid]<value){
low = mid + 1;
}else{
high = mid -1;
}
}
return -1;
}
/*递归实现*/
public int binarySearchByRecursion(int[] a,int low,int high,int value){
if(low > high) return -1;
int mid = low+((high-low)>>2);
if(a[mid] == value) return mid;
if(a[mid]<value){
return binarySearchByRecursion(a,mid+1,high, value);
}else{
return binarySearchByRecursion(a,low,mid-1, value);
}
}
3.二分查找变形
变形1:查找第一个值等于给定值的元素
/*二分查找变形1:查找第一个值等于给定值的元素*/
public int binarySearchOne(int[] a, int value){
int low = 0;
int high = a.length-1;
int mid = 0;
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] == value){
if(mid == 0 || a[mid-1] != value) return mid;
else high = mid -1;
}else if(a[mid]<value){
low = mid + 1;
}else{
high = mid -1;
}
}
return -1;
}
变形2:查找最后一个值等于给定值的元素
/*二分查找变形2:查找最后一个值等于给定值的元素*/
public int binarySearchTwo(int[] a, int value){
int low = 0;
int high = a.length-1;
int mid = 0;
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] == value){
if(mid == a.length-1 || a[mid+1] != value) return mid;
else low = mid +1;
}else if(a[mid]<value){
low = mid + 1;
}else{
high = mid -1;
}
}
return -1;
}
变形3:查找第一个值大于等于给定值的元素
/*二分查找变形3:查找第一个值大于等于给定值的元素*/
public int binarySearchThree(int[] a, int value){
int low = 0;
int high = a.length-1;
int mid = 0;
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] >= value){
if(mid == 0 || a[mid-1] < value) return mid;
else high = mid -1;
}else{
low = mid + 1;
}
}
return -1;
}
变形4:查找第一个值小于等于给定值的元素
/*二分查找变形4:查找最后一个值小于等于给定值的元素*/
public int binarySearchFour(int[] a, int value){
int low = 0;
int high = a.length-1;
int mid = 0;
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] <= value){
if(mid == a.length-1 || a[mid+1] > value) return mid;
else low = mid +1;
}else{
high = mid - 1;
}
}
return -1;
}
4.案例
1.1000万个整数,每个整数占 8 个字节,判断某个是否在数组中,内存只有100MB
1000万整数,大概80MB,完全可以先对其排序,再用时间复杂度为O(logn)的二分查找法查找;
2.求一个整数的平方根,保留6位小数
方案:中间值mid的平方mid*mid和初始值比较,求他们的插值offset,如果offset >= 0.000001则继续折半查找,否则跳出循环,则就是精确到第六位小数;
3.通过 IP 地址来查找 IP 归属地,假设我们有 12 万条这样的 IP 区间与归属地的对应关系,如何快速定位出一个 IP 地址的归属地呢?
[202.102.133.0, 202.102.133.255] 山东东营市
[202.102.135.0, 202.102.136.255] 山东烟台
[202.102.156.34, 202.102.157.255] 山东青岛
[202.102.48.0, 202.102.48.255] 江苏宿迁
[202.102.49.15, 202.102.51.251] 江苏泰州
[202.102.56.0, 202.102.56.255] 江苏连云港
方案:
- 我们可以把每个区间的最小值和IP归属地形成一个映射关系
- 把最小值放入数组中排序
- 二分查找法获取 最后一个小于等于 输入IP地址的值
- 返回第一步映射关系中对应的值
4.如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?
遍历获取最大值,最大值就是分界点,然后二分查找;
/*如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。
* 针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?
* 1. 遍历得到最大值,作为分界点
* 2. 二分查找
*/
public int binarySearchCircle(int[] a,int value){
int low = 0;
int high = a.length-1;
int mid = 0;
for (int i = 0; i < a.length-1; i++) {
if(a[i]>a[i+1]){
high = i;
break;
}
}
if(a[high] == value) return high;
if(a[low] == value) return low;
if(a[low] > value){
low = high + 1;
high = a.length - 1;
}else{
high = high - 1;
}
while(low<=high){
mid = low+((high-low)>>2);
if(a[mid] == value) return mid;
if(a[mid]<value){
low = mid + 1;
}else{
high = mid -1;
}
}
return -1;
}
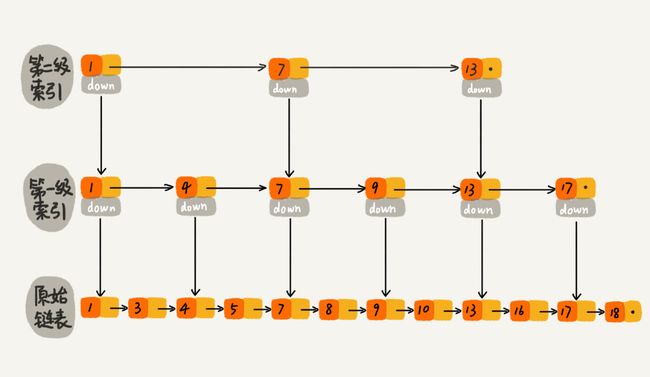
8.跳表(skip list)-链表结构的二分查找O(logn)
1.跳表特性
二分查找依赖数组的随机访问,且要求数组有序,它查找的时间复杂度是O(logn)
如何用链表实现二分查找的O(logn)的时间复杂度?
跳表这种数据结构,可以实现查找为O(logn);
- 跳表查找时间复杂度为O(logn)
- 可以支持快速地插入、删除、查找操作
2.跳表原理
1.时间复杂度和空间复杂度
跳表引入索引结构的概念;
如果每两个节点加一个索引,那么,第一级索引有n/2个节点,第二级有n/4个节点,第k级有n/(2k)个节点(最后一级2个节点),那么2=n/(2k),k=log2n-1。
查询时间复杂度为log(n);
额外增加n/2+n/4+…+2 个节点,约等于n个节点,那么空间复杂度为O(n);
思考:为什么空间复杂度那么高,还要引入跳表这种数据结构呢?
在实际开发中,往往存储的占用内存较大的对象,而我们建立的索引节点存储的是关键值和几个指针,并不会消耗太大内存,还能获得高效的查询;
2.插入删除效率
我们知道单链表的插入效率为O(1),但是查找插入位置前一个节点的时间复杂度为O(n);
而跳表的插入效率也为O(1),查找前一个元素的时间复杂度为O(logn);
3.索引动态更新
假如跳表每三个节点加一个索引,那么如果插入元素过多呢?是不是意味着查询部分区间耗时过多?
为了索引均匀分布,不会出现部分区间臃肿的情况,跳表会动态更新索引;
插入节点,会通过随机函数,决定需要添加到哪几级索引,假如随机函数获得数字为K,那么就会把插入节点放入第1~k级的索引中;
4.redis为什么使用跳表实现有序集合,而不用红黑树?
-
有序集合按照区间来查找数据这个操作,红黑树的效率没有跳表高
-
跳表容易实现,简单灵活
9.散列表O(1)
1.散列表和散列函数
散列函数,顾名思义,它是一个函数。我们可以把它定义成 hash(key),其中 key 表示元素的键值,hash(key) 的值表示经过散列函数计算得到的散列值。
构造散列函数的基本要求:
- 散列函数计算得到的散列值是一个非负整数
- 如果 key1 = key2,那 hash(key1) == hash(key2)
- 如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2)
然而现实生活中第三条几乎很难满足,那么就一定会出现 散列冲突(也叫hash碰撞)
解决散列冲突有两种方法:
- 开放寻址法
- 链表法
2.散列冲突
1.开放寻址法
出现散列冲突就重新探测一个空闲位置,插入;
那么如何一个新的探测空闲位置呢?
- 线性探测法:往后遍历数组,直到找到空闲位置
- 二次探测:二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22……
- 双重散列:使用一组散列函数 hash1(key),hash2(key),hash3(key)进行散列
ThreadLocalMap通过线性探测的开放寻址法来解决冲突;
优点:散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度;
缺点:
- 删除数据麻烦,需要特殊标记删除的元素;
- 由于只存数组中,所以装载因子上限不能太大
- 比链表法更耗内存
总结:当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。
2.链表法
数组+链表
LinkedHashMap使用链表法
优点:内存利用率高,对装载因子的容忍度高
缺点:由于要存储指针,比较消耗内存
链表法改造为更高效的散列表就是 跳表,红黑树了;
总结:基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表,而且,比起开放寻址法,它更加灵活,支持更多的优化策略,比如用红黑树代替链表。
3.如何实现一个工业级的散列表?
hash函数设计,装载因子,hash冲突都会影响 散列表的执行效率;
1.hash函数设计
尽量使数据均匀分布;
2.如何合理设置装载因子?
装载因子过大:扩容
装载因子过小:如果空间不够用,就缩容;否则可以不处理
3.如何避免低效扩容?
当装载因子接近阈值,进行扩容机制;如何这时候有频繁插入操作,我们在插入时选择一次性扩容,插入效率极低,所以要避免一次性扩容;
我们可以插入一条数据,然后从旧(old)散列表去一个数据放入新(new)的散列表,边插入边扩容;
查找时,现在新表中查,没有的话再去旧表查;
4.工业级散列表hashMap
- 初始大小:默认16,可以手动设置
- 装载因子和动态扩容:默认0.75,当元素个数超过0.75*capacity(散列表容量),每次扩容为原来的两倍
- 散列冲突解决方法:桶内元素超过8,旋转为红黑树,小于8退化为链表
4.数组+链表组合
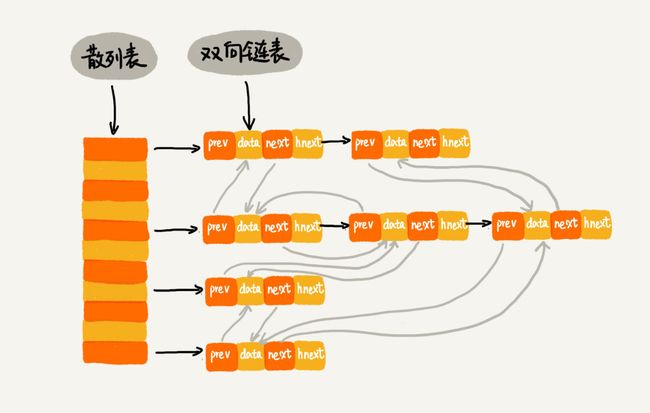
1.如何实现一个高效查找,插入,删除的LRU缓存系统?
之前我们讲可以用数组和链表实现一个 查找,插入,删除 时间复杂度为O(n)的LRU缓存结构;
这次来实现一个时间复杂度为O(1)的LRU;
方案:数组+双向链表;
hnext表示连接作用,把双向链表中不是相邻的两个节点连接起来,使每个槽内节点 连贯起来;
插入时,获取散列值,找到所在槽位,遍历链表,没有的话,插入双向链表尾部,在对应槽内用 tail.hnext = 插入数据节点;
删除时,获取散列值,找到所在槽位,找到节点,直接删除(由于是双向链表,所以删除时间复杂度O(1))
查找时,获取散列值,找到所在槽位,找到节点
散列表满时,直接删除双向链表头部数据,新值插入尾部
2.Redis有序集合的实现
redis实现用跳表+散列表实现,在有序集合中,每个成员对象有两个重要的属性,key(键值)和 score(分值)
跳表高效实现了4,5两个功能, 散列表高效实现了1,2,3两个功能
Redis有序集合功能:
- 支持key值获取数据
- 支持key值,删除数据
- 添加一个成员
- 根据score使数据从小到大排序(数据有序)
- 可以区间取值(例如:获取score在[100-230]之间的数据)
3.Java LinkedHashMap
实现:数组+双向链表(以及LRU缓存淘汰思想)
LinkedHashMap 中的“Linked”实际上是指的是双向链表,并非指用链表法解决散列冲突。
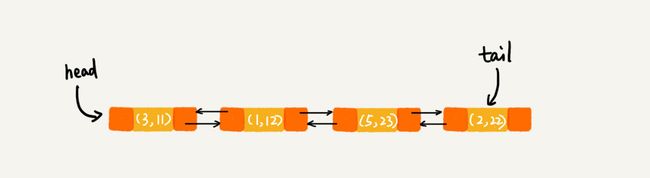
// 10是初始大小,0.75是装载因子,true是表示按照访问时间排序
HashMap<Integer, Integer> m = new LinkedHashMap<>(10, 0.75f, true);
m.put(3, 11);
m.put(1, 12);
m.put(5, 23);
m.put(2, 22); ①
m.put(3, 26); ②
m.get(5); ③
for (Map.Entry e : m.entrySet()) {
System.out.println(e.getKey());
}
输出结果:1,2,3,5
执行到 ① 时:
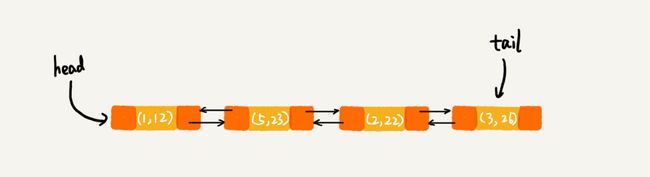
执行到②时,linkedHashMap会 获取3的hash值,把原来节点(3,11)删除,然后把(3,26插入末尾)
执行到③时,linkedHashMap会 获取5的值,把原来节点(5,23)移动到链表尾部
总结:
散列表这种数据结构虽然支持非常高效的数据插入、删除、查找操作,但是数据无序
为了让数据有序,我们引入链表(或者跳表),散列表+链表结合
5.案例
1.word文档如何实现检查英文单词拼写正确?
常用的英文单词有 20 万个左右,平均一个单词占用 10 个字节的内存空间,那 20 万英文单词大约占 2MB 的存储空间,就算放大 10 倍也就是 20MB。
所以,讲英文单词放入散列表存储,检查;
2.假设我们有 10 万条 URL 访问日志,如何按照访问次数给 URL 排序?
URL为key,次数为value放入散列表,获取最大值maxValue;
如果maxValue比较大,快排;
否则,桶排序;
3.有两个字符串数组,每个数组大约有 10 万条字符串,如何快速找出两个数组中相同的字符串?
以第一个字符串数组构建散列表,key 为字符串,value 为出现次数。再遍历第二个字符串数组,以字符串为 key 在散列表中查找,如果 value 大于零,说明存在相同字符串。时间复杂度 O(N)。
4.设计一个数据结构完成以下要求
假设猎聘网有 10 万名猎头,每个猎头都可以通过做任务(比如发布职位)来积累积分,然后通过积分来下载简历。假设你是猎聘网的一名工程师,如何在内存中存储这 10 万个猎头 ID 和积分信息,让它能够支持这样几个操作:
- 根据猎头的 ID 快速查找、删除、更新这个猎头的积分信息;
- 查找积分在某个区间的猎头 ID 列表;
- 查找按照积分从小到大排名在第 x 位到第 y 位之间的猎头 ID 列表。
10.哈希算法
1.哈希算法的特点
哈希就是能够把不同长度二进制的数据加密成相同长度的二进制数据的一种算法;
128位二进制有2128个组合,那么哈希算法在最理想的情况下,就能计算出最多2128个数据,且没有hash冲突;
- 不同的字符串(无论字符串长度是多少)加载成相同长度的数据
- hash算法加载后的字符串不可逆,很难推算出原来的字符串
- 要求计算的hash值尽可能的分布均匀,不冲突
- 要求有较高的执行效率
2.hash算法的使用场景
1.安全加密
用户信息加密,但是有些用户数据密码设置比较简单,容易被撞库破解,
一般会把用户信息和盐salt 一块加密存储
2.文件块校验
下载电影时,把电影文件分成多个块,每个块有两个区域,一部分存储上一个文件块的hash值,另一部分存储数据;
当文件块别篡改时,那么hash值一定会改变,就会校验不成功,重新下载文件块。
3.hash函数
hash’map,等用到散列表的数据都用到了hash算法,但是这种hash算法对hash冲突和执行效率要求要对较低
4.唯一标识
我们从海量图片数据中判断某个图片是否存在?
由于图片二进制太大,可以取图片部分数据(比如取前中后100个字节),用这些信息摘要,进行hash处理,生成唯一标识,放入hash表中,key为图片hash值,value为图片路径;
5.负载均衡
分布式环境下,有很多负载均衡的算法,比如:轮询,加权轮询,随机
我们如何实现 “会话粘滞”呢?(就是同一客户端同一会话 的请求都发送到同一个服务器上)
对客户端IP地址做hash处理,然后与 服务器数量n取模
6.分布式缓存
1.如何统计“搜索关键词”出现的次数?
假如我们有 1T 的日志文件,这里面记录了用户的搜索关键词,我们想要快速统计出每个关键词被搜索的次数,该怎么做呢?
1T证明单台机器内存肯定不够,那么就用多台机器;
遍历日志文件,将字符串取hash值 与服务器取模,这样就把相同的字符串放到了相同的机器上,然后根据hash值放入散列表中,key为字符串,value为次数
7.分布式存储
假如我们要把1亿张图片放入缓存,分别存放在10台机器,但是如果我们想要添加3台服务器,或者有三台服务器同时挂掉了怎么办?
hash值与机器数取模,当机器数变了,那么原来的图片就会缓存到别的服务器;当有大量请求同时过来,就会出现缓存雪崩的现象;
怎么解决?这时候就需要用“一致性哈希算法了”
3.一致性哈希算法
链接:白话一致性哈希算法
- 不再是取数据的hash的值与机器数取模,而是把机器的IP取hash与2^32取模,放在hash圆环上
- 数据的hash值也是与2^32取模投放在hash圆环上,顺时针找到的第一个机器就把数据存上去
- 这样当有机器 增减时,避免全部缓存失效,牺牲了一小部分缓存
- 但是机器数量与2^32比太小了,导致机器分布不均匀,那么就引入了虚拟节点,使缓存均匀分布在机器上