【算法】BFS 广度优先遍历由浅入深
//该算法比较重要,看文字的时候最好集中注意力,看不懂多敲几遍代码,对图不了解的可以先百度一下
图的广度优先遍历类似于树的层次遍历,采用的搜索方法的特点是尽可能先对横向结点进行搜索,故称其为广度优先搜索(Breadth-First-Search).
其基本思想是:
给定图 G= (V, E) 从图中某个源点v出发,在访问了顶点V之后接着就尽可能先在横向搜索V的所有邻接点。在依次访问V的各个未被访问的邻接点w1,w2,....,wk之后,分别从这些邻接点出发依次访问与w1,w2,...,wk邻接的所有未访问过的顶点。依次类推,直至图中所有和源点V有路径相通的顶点都已经访问过为止,此时从V开始的搜索过程结束。若G是连通图,则遍历完成;否则,在图G中另选一个尚未访问的顶点作为新源点继续上述的搜索过程,直至图G中所有顶点均已被访问为止。
采用广度优先搜索法遍历图的方法称为图的广度优先遍历。
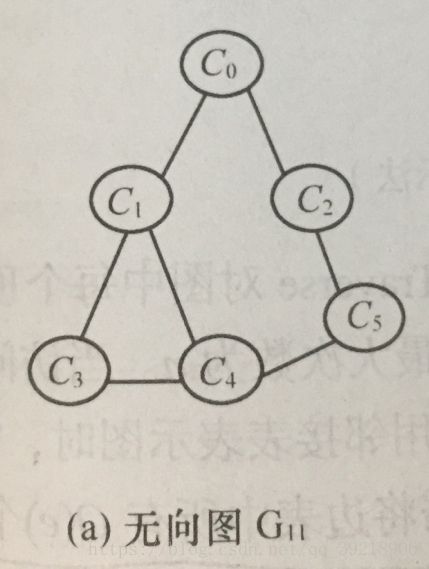
对如图所示的无向图G11进行广度优先遍历的过程为:首先访问起始点,假设从C0出发,接着访问与C0邻接的顶点C1和C2,然后依次访问与C1邻接的未曾访问的顶点C3和C4,最后访问与C2;邻接的顶点C5。至此,这些顶点的邻接点均已被访问,并且图中的所有顶点都已被访问,图的遍历结束,得到该图的广度优先遍历(简称BSF序列)为:
C0->C1->C2->C3->C5
为确保先访问的顶点其邻接点亦先被访问,在搜索过程中可使用队列来保存已访问过的顶点。当访问V和u时,这两个顶点相继入队,此后,当V和u相继出队时,分别从V和u出发搜索其邻接点V1,V2,..,Vs和u1,u2,..ut,对其中未访者进行访问并将其入队。这种方法是将每个已访问的顶点入队,保证邻每个顶点至多只有一次入队
若图采用邻接表存储结构,则算法如上图的广度优先遍历算法可表示如下
//图的广度优先遍历算法 文件名bfs.c
#include "ljb.h"
int visited[M]; //全局标志向量
//函数功能:从顶点i出发广度优先变量图g的连通分量
//函数参数:图的邻接表g,遍历始点i
//函数返回值:无
void bfs(linkedGraph g,int i)
{
int j;
EdgeNode *p;
int queue[M],front,rear; //FTFO队列
front = rear = 0; //初始化空队列
printf("%c",g.adjlist[i].vertex); //访问源点
visited[i] = 1;
queue[rear++] = i; //被访问结点进队
while (rear > front) //当队列非空时,执行下列循环体
{
j = queue[front++]; //出队
p = g.adjlist[j].FirstEdg;
while (p)
{
if (visited[p ->adjvex] == 0)
{
printf("%c",g.adjlist[p ->djvex].vex);
queue[rear++] = p->adjvex].vertex);
queue[rear++] = p ->adjvex;
visited[p->adjvex] = 1;
}
p = p->next;
}
}
}
//函数功能:广度优先遍历图g
//函数参数: 邻接表g
//函数返回值:返回连通分量的个数
int BfsTrverse(LinkedGraph g)
{
int i,count = 0;
for (i = 0;i < g.n;i++)
visited[i] = 0; //初始化标志数组
for (i = 0;i < g.n;i++)
if (!visited[i]) //Vi未被访问过
{
printf{"\n");
count++; //连通分量个数加1
bfs(g,i);
}
return count;
}
int main()
{
LinkedGraph g;
int count;
creat(&g,"g11.txt",0);
printf("\n The graph is:\n"); //假设G11 的图信息存储在g11.txt文件中
print(g); //输出图的邻接表
count = BfsTraverse(g); //从顶点0出发广度优先遍历图g
printf("\n该图共有%d个连通分量。\n",count);
return 0;
}对于具有n个顶点和e条边的无向图或有向图,每个顶点均入队一次。广度优先遍历图的时间复杂度和DfsTraverse算法相同。另外,广度优先遍历无向图的过程中调用bfs的次数就是该图的连通分量的个数,当图g是连通图(强连通图)时,只需从一个源点出发就可以遍历完图中所有的顶点,函数BfsTraverse借助广度优先遍历图的过程返回无向图的连通分量个数。
了解了该算法后下面
用BFS求最短路
假设有一个网格迷宫,由n行m列的单元格组成,每个单元格要么是空地(用1 来表示),要么是障碍物(用0来表示)。如何找到从起点到终点的最短路径?
还记得二叉树的BFS吗?结点的访问顺序恰好是它们到根结点距离从小到大的顺序。类似地,也可以用BFS来按照到起点的距离顺序遍历迷宫图。
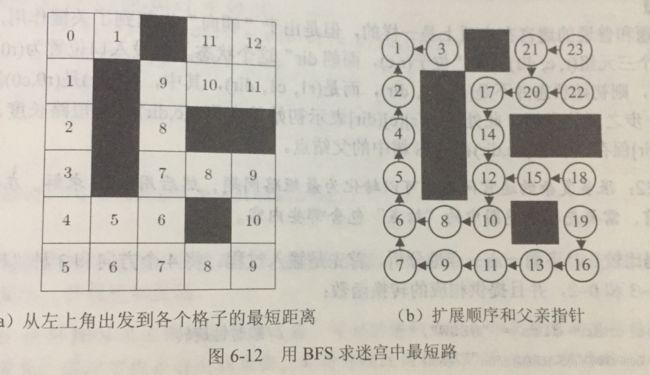
例如,假定起点在左上角,就从左上角开始用BFS遍历迷宫图,逐步计算出它到每一个结点的最短路距离(如图所示(a)),以及这些最短路径上每个结点的“前一个结点”(如图(b)所示)
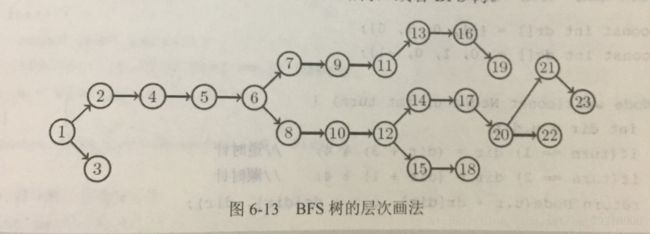
注意,如果把图(b) 中箭头理解成“指向父亲的指针”,那么迷宫中的格子就变成了一棵树——除了起点之外,每个结点恰好有一个父亲。如果看不出来。可以把这棵树画成如图6-13所示的样子。这棵树称为最短路树,或者BFS树。
例题Abbot的复仇(Abbtt's Revenge,ACM/ICPC World Finals 2000,Uva 816)
有一个最多包含9*9个交叉点的迷宫。输入起点、离开起点时的朝向和终点,求一条最短路(多解时任意输出一个即可)
这个迷宫的特殊之处在于;
进入一个交叉点的方向(用NEWS这4个字母分别表示北东西南,即上右左下)不同,允许出去的方向也不同。
例如,12WLF NR ER *表示交叉点(1,2)(上数第1行,左数第2列)有3个路标(字符”*“只是结束标志),如果进入该交叉点时的朝向为W(即朝向左),则可以左转(L) 或者直行(F);如果进入时朝向为N或者E则只能右转(R) ,如图6-14所示。
注意:
初始状态是”刚刚离开入口:,所以即使出口和入口重合,最短路也不为空。例如,图6-14中的一条最短路为
(3,1)(2,1)(1,1)(1,2)(2,2)(2,3)(1,3)(1,2)(1,1)(2,1)(2,2)(1,2)(1,3)
(2,3)(3,3)。
【分析】
本题和普通的迷宫在本质上一样的,但是由于“朝向”也起到了关键作用,所以需要用一个三元组(r,c,dir)表示“位于(
(r,c),面朝dir"这个状态。假设入口位置为(r0,c0),朝向为dir,则初始状态并不是(r0,c0,dir),而是(r1,c1,dir),其中,(r1,c1)是(r0,c0)沿着方向dir走一步之后的坐标。此处用d[r][c][dir]表示初始状态到(r,c,dir)的最短路长度,并且用p[r][c][dir]保存路状态(r,c,dir)在BFS树种的父结点。
提示6-22
很多复杂的迷宫问题都可以转化为最短路问题,然后用BFS求解。在套用BFS框架之前,需要先搞清楚图中的”结点“包含哪些内容。
代码比较长,下面一点一点地分析。首先是输入过程。将4个方向和3种”转弯方式“编号为0-3和0-2,并且提供对应的转换函数。
const char* dirs = "NESW"; //顺时针旋转
const char* turns = "FLR";
int dir_id(char c)
{
return strchr(dirs,c) - dirs;
}
int turn_id(char c)
{
return strchr(turns,c) - turns;
}
//接下来是”行走“函数,根据当前状态和转弯方式,计算出后继状态:
const int dir[] = {-1,0,1,0};
const int dc[] = {0,1,0,-1};
Node walk(const Node& u,int turn)
{
int dir = u.dir;
if(turn == 1)
dir = (dir + 3) % 4; //顺时针
if(turn == 2)
fir = (dir + 1) % 4; //逆时针
return Node(u.r + dr[dir],u.c + dc[dir],dir);
}
//输入函数比较简单,作用就是读取r0,c0,dir,并且计算出r1,c1,然后读入has_edge数组,其中has_edge[r][c]dir][turn]
//表示当前状态是(r,c,dir),是否可以沿着转弯方向turn行走。下面是BFS主过程:
void solve()
{
queue q;
memset(d, -1,sizeof(d));
Node u(r1,c1,dir);
d[u.r][u.c][u.dir] = 0;
q.push(u);
while(!q.empty())
{
Node u = q.front();q.pop();
if(u.c == r2 && u.c == c2)
{
printf_ans(u);
return;
}
for(int i = 0;i < 3;i++)
{
Node v = walk(u,i);
if(has_edge[u.r][u.c][u.dir][i] && inside(v.r,v.c)
&& d[v.r][v.c][v.dir] < 0)
{
d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;
p[v.r][v.c][v.dir] = u;
q.push(v);
}
}
}
printf("No Solution Possible\n");
}
//最后是解的打印过程。它也可以写出递归函数,不过用vector保存结点可以避免递归时出现栈溢出,并且更加灵活。
//提示6-23:使用BFS求出图的最短路之后,可以用递归方式打印最短路的具体路径。
//如果最短路非常长,递归可能会引起栈溢出,此处可以改用循环,用Vector
void printf_ans(Node u)
{
//从目标结点逆序追溯到初始结点
vector nodes;
for(;;)
{
nodes.push_back(u);
if(d[u.r][u.c][u.dir] == 0)
break;
u = p[u.r][u.c][u.dir];
}
nodes.push_back(Node(r0,c0,dir));
//打印解,每行10个
int cnt = 0;
for (int i = nodes.size() -1;i >= 0;i --)
{
if(cnt % 10 == 0)
printf(" ");
printf("(%d,%d)",nodes[i].r,nodes[i].c);
if(++cnt % 10 == 0)
printf("\n");
}
if(nodes.size() % 10 != 0)
printf("\n");
}
//本题非常重要,强烈建议读者搞懂所有细节,并能独立编写程序
下面趁热打铁再做一个ACM练习
It’s universally acknowledged that there’re innumerable trees in the campus of HUST.
And there are many different types of trees in HUST, each of which has a number represent its type. The doctors of biology in HUST find 4 different ways to change the tree’s type x into a new type y:
1. y=x+1
2. y=x-1
3. y=x+f(x)
4. y=x-f(x)
The function f(x) is defined as the number of 1 in x in binary representation. For example, f(1)=1, f(2)=1, f(3)=2, f(10)=2.
Now the doctors are given a tree of the type A. The doctors want to change its type into B. Because each step will cost a huge amount of money, you need to help them figure out the minimum steps to change the type of the tree into B.
Remember the type number should always be a natural number (0 included)..
//做完后可以看下答案
#include
using namespace std;
const int maxn=1000000+500;
const int INF = 0x3f3f3f3f;
bool vis[maxn];
int ans[maxn];
queue q;
int a,b;
int f(int x){
int n;
for(n=0; x; n++) x &= x-1;
return n;
}
void bfs(){
for(int i=0;i>a>>b;
bfs();
cout<
//该文章部分摘录于《数据结构》(李云清)《算法竞赛入门经典》(刘汝佳)