一文弄懂数据结构中的红黑树、二叉树

前言

红黑树

在讲红黑树之前，我们需要先了解几种树：二叉树，二叉查找树以及平衡二叉树。

二叉树

最多有 2 个孩子的树称为二叉树。由于二叉树中的每个元素只能有 2 个孩子，我们通常将它们命名为左孩子和右孩子。

• 示意：

      5
    /	\
   2     3	
复制代码

• 代码定义：

class Node {
    T data;
    Node left;
    Node right;
}
复制代码

二叉查找树

二叉查找树（Binary Search Tree，简称BST），（又：二叉搜索树，二叉排序树） 它是一种基于节点的二叉树数据结构，具有以下特性：

1. 节点的左子树仅包含值小于节点值的节点。
2. 节点的右子树仅包含值大于节点值的节点。
3. 左右子树也必须是二叉查找树。

• 示意：

  						  5
  						/    \
  						2     6	
  					       / \
  					      1   3
  						  \
  						   4
  复制代码

一颗平衡的 BST 查找效率很高，原理就是二分查找，二分查找的时间复杂度为 O(log n)。

二叉查找树退化成链表

当我们插入一组元素正好是有序的时候，这时会让排序二叉树退化成链表。如下所示:

					 1	  
					  \	
					   2     	
					    \
					     3
					      \
					       4
复制代码

这样排序二叉树退化成链表结构，那么检索效率就变成了线性的 O(n) 的，相对来说，检索效率肯定是要差不少的。

平衡二叉树

平衡二叉树 (AVL) 树是一种自平衡二叉查找树 (BST)，并且其中所有节点的左右子树的高度差不能超过 1。

平衡二叉树在二叉查找树的基础上多了一个特性：所有节点的左右子树的高度差不能超过 ；从而实现自平衡。

AVL树示意：

				    13
				   /  \
				  8    18
				 / \     \
				6   10    20
			       /
			      4
复制代码

大多数 BST 操作（例如，搜索、最大、最小、插入、删除等）花费 O(h) 时间，其中 h 是 BST 的高度。对于偏斜二叉树，这些操作的成本可能变为 O(n)。如果我们确保每次插入和删除后树的高度都保持 O(Logn)，那么我们可以保证所有这些操作的上限为 O(Logn)。AVL 树的高度始终为 O(Logn)，其中 n 是树中的节点数。

红黑树

• 介绍：

红黑树是一种自平衡二叉搜索树，每个节点都有一个额外的位置用来存储节点的颜色（红色或黑色）。这些颜色用于确保树在插入和删除过程中保持平衡。虽然树的平衡性并不完美，但足以减少搜索时间并保持在 O(log n) 时间左右，其中 n 是树中元素的总数。红黑树是由鲁道夫·拜耳 (Rudolf Bayer) 于 1972 年发明的。

其实红黑树和上面的平衡二叉树类似，本质上都是为了解决排序二叉树在极端情况下退化成链表导致检索效率大大降低的问题。

红黑树的特性

1. 每个节点要么是红色，要么是黑色。
2. 根节点永远是黑色的。
3. 所有的叶子节点都是空节点（即null），并且是黑色的。
4. 没有两个相邻的红色节点（红色节点不能有红色父节点或红色子节点）。
5. 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

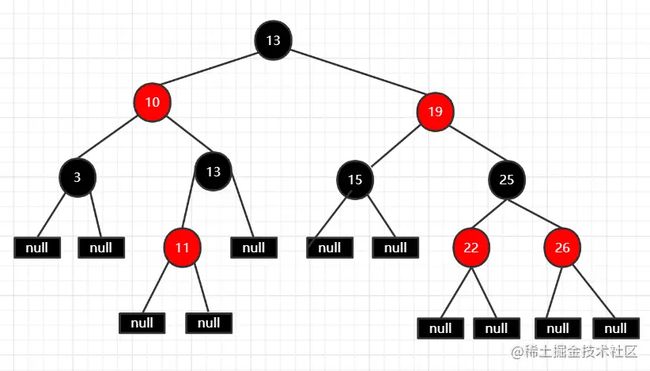
红黑树示意图：

``

对于3 中指定红黑树的每个叶子节点都是空节点，而且叶子节点都是黑色，但 Java 实现的红黑树会使用 null 来代表空节点，因此我们在遍历 Java里的红黑树的时候会看不到叶子节点，而看到的是每个叶子节点都是红色的，这一点需要注意。

由第5条：

• 从任一节点到它的子树的每个叶子节点黑色节点的数量都是相同的，这个数量被称为这个节点的黑高
• 从根节点出发到每个叶子节点的路径都包含相同数量的黑色节点，这个黑色节点的数量被称为树的黑高

我们知道 AVL 树 所有节点的左右子树的高度差不超过 1， 在这里我们思考一个问题，对于红黑树任意节点左右树的高度差是多少呢？

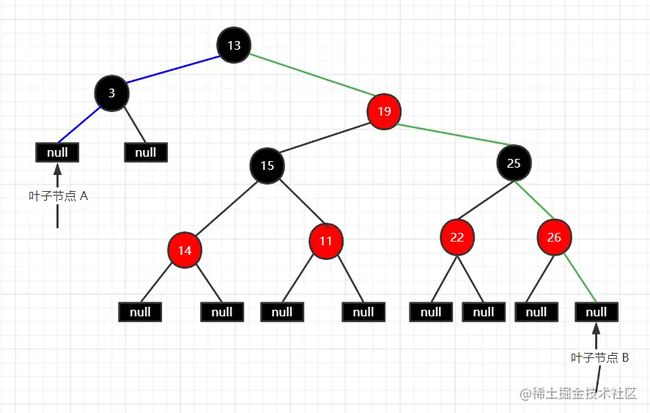
看下面的这个红黑树：

依次验证上面5条特性，

1. 每个节点要么是红色，要么是黑色。
2. 根节点永远是黑色的。
3. 所有的叶子节点都是空节点（即null），并且是黑色的。
4. 没有两个相邻的红色节点（红色节点不能有红色父节点或红色子节点）。
5. 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

发现都可以满足。

事实上，以上是红黑树中比较极端的一个例子，该树在满足红黑树特性的前提下，左子树达到了最小高度（全黑） ，右子树达到了最大高度（一层黑一层红，红黑交替） ；分别是 2 和 4；

也就是说，一个黑高为 3 的红黑树 ，其最小高度为3，最大高度为 5；同时其子树最小高度为 2，最大高度为 4。

从一个节点到其最远后代叶的节点数不超过到最近后代叶节点数的两倍；可以这么简单理解，红黑树根节点到叶子节点最长的路径都不会比最短的路径长出两倍。

红黑树 VS AVL树

与红黑树相比，AVL 树更平衡，但它们在插入和删除过程中可能会导致更多的旋转。所以如果涉及频繁的插入和删除，那么红黑树应该是首选。如果插入和删除不那么频繁并且搜索是一个更频繁的操作，那么 AVL 树应该比红黑树更合适。

红黑树的应用

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。 例如，Java集合中的 TreeSet 和 TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

插入

当我们向红黑树中插入新的元素时，红黑树发生变化，有可能不再满足那5个条件，不再平衡；我们有两种方法使其重新恢复平衡：重新着色、旋转。

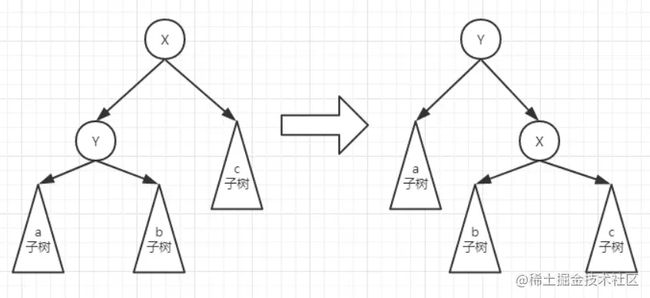
其中旋转分为左旋和右旋

• 对X左旋：

• 对X右旋：

为了避免混淆，接下来使用图示的叫法：

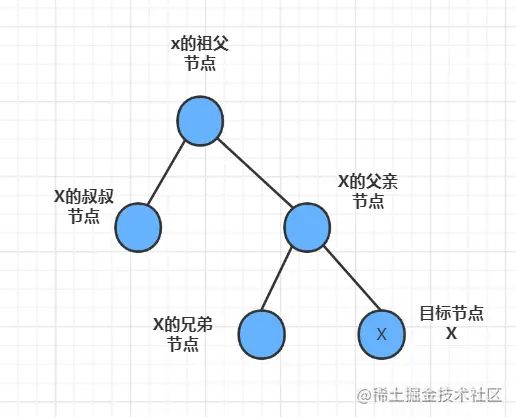
设 X 为新插入的节点，完整步骤为：

一、按照二叉查找插入方法将 X 插入到指定的位置，并将新插入节点的颜色设为红色。

二、如果 X 是根节点，则将 X 的颜色更改为黑色。

三、被 X 节点的父节点是黑色，什么都不需要做。

四、被 X 节点的父节点是红色（该情况与红黑树的“特性(4)”相冲突）：

​ a) 如果 x 的叔叔节点是红色的

1. 将父节点和叔叔节点的颜色更改为黑色
2. 将祖父节点设为红色
3. 令 x = 祖父节点，对新的 x 重复以上步骤

​ b) 如果 x 的叔叔节点是黑色的，分别对应下面四种不同情况

1. 左左案例（LL 旋转）
2. 左右案例（LR 旋转）
3. 右右案例（RR 旋转）
4. 右左案例（RL 旋转）

以上就是插入的所有步骤，接下来举例分析以上几种情况：

叔叔节点为红色：

这种情况不需要旋转，只需要对父节点，叔叔节点，祖父节点重新染色即可。注意，由于祖父节点重新染色后有可能会破坏掉之前的平衡，所以我们需要对祖父节点重复这个染色操作，使其始终满足5条特性。

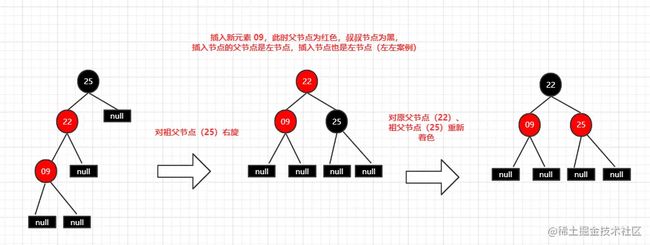
左左案例（插入节点的父节点是左节点，插入节点也是左节点）

1. 对祖父节点右旋
2. 重新着色

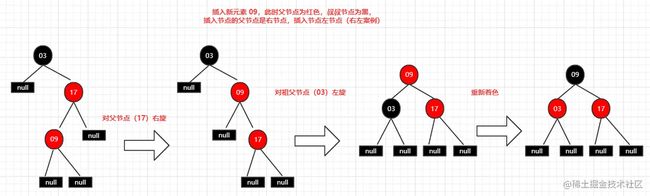
左右案例（插入节点的父节点是左节点，插入节点是右节点）

1. 对父节点左旋
2. 对祖父节点右旋
3. 重新染色

右右案例（插入节点的父节点是右节点，插入节点左节点）

1. 对祖父节点左旋
2. 重新染色

右左案例（插入节点的父节点是右节点，插入节点左节点）

1. 对父节点右旋
2. 对祖父节点左旋
3. 重新着色

删除

与插入一样，利用重新着色、旋转来保持红黑树平衡。 在插入操作中，我们检查叔叔节点的颜色来决定合适的情况。在删除操作中，我们检查兄弟节点的颜色来决定合适的情况。

插入新元素后违反的主要属性是两个连续的红色。在删除中，主要违反的性质是，子树中黑色高度的变化，因为删除一个黑色节点可能会导致一个根到叶路径的黑色高度降低。

删除是一个相当复杂的过程。为了方便理解，使用了双黑的概念。当一个黑色节点被删除并被一个黑色子节点替换时，这个子节点被标记为双黑（在本文中，双黑意味着节点的黑高不再平衡，需要调整，这里只是一种叫法而已，并没有什么其他的含义）。这是会引起黑高改变的情况，也是我们需要重点关注的情况。

删除的详细步骤：

1) 执行标准 BST 删除. 当我们在 BST 中执行标准删除操作时，最终将删除一个节点，它要么是叶子节点，要么只有一个子节点（对于内部节点，我们复制后继节点，然后递归调用后继节点的删除，后继节点始终是叶子节点或有一个孩子的节点）。所以我们只需要处理节点是叶子节点或有一个子节点的情况。设 v 是要删除的节点，u 是替换 v 的子节点（注意，当 v 是叶子时，u 是 NULL，NULL 的颜色被认为是黑色）。

2) 如果 u 或 v 是红色，我们只需要将替换上来的节点标记为黑色（黑色高度没有变化）。请注意，u 和 v 不能都是红色，因为 v 是 u 的父级，红黑树中不允许出现两个连续的红色。如下图：

3) 如果 u 和 v 都是 Black。

3.1）如果u是根节点，什么都不需要做。（树的黑高减 1）

3.2）出现双黑，设 U 的兄弟节点为 s。

…… (a): 如果兄弟节点 s 是黑色并且兄弟的至少一个孩子是红色，则执行旋转。设 s 的红色孩子是 r。根据 s 和 r 的位置，这种情况可以分为四个子情况。

…………..(i) 左左案例（s 是其父级的左孩子，r 是 s 的左孩子，或者 s 的两个孩子都是红色的）。这是下图所示的右右案例的镜像。

………….. (ii) 左右案例（s 是其父母的左孩子，r 是右孩子）。这是下图所示的右左案例的镜像。

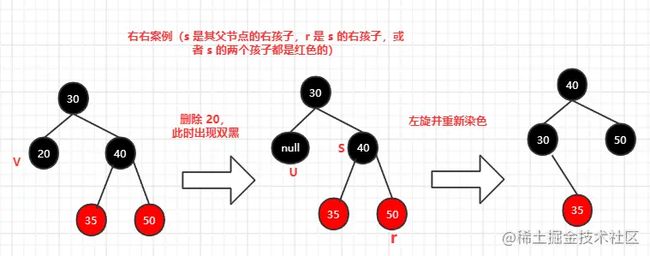
……………(iii) 右右案例（s 是其父节点的右孩子，r 是 s 的右孩子，或者 s 的两个孩子都是红色的）

………….. (iv) 右左案例（s 是其父节点的右孩子，r 是 s 的左孩子）

..... (b): 如果兄弟 s 是黑色的，并且它的两个孩子都是黑色的，则需要染色，如果父级 P 也是黑色，则需要父级递归染色。

在这种情况下，如果父节点 P 为红色，我们只需要将其设置为黑色，不再需要递归。

..... (c): 如果兄弟是红色的，则执行旋转要向上移动旧兄弟节点，对旧兄弟节点和父级节点重新染色。新的兄弟节点一定是黑色的（见下图，看图容易明白）。这时候，将会出现我们在 （a）或 （b）中分析过的情况，按照上面的分析步骤继续就可以了。这种情况又可以分为两个子情况。

………….. (i) 左案例（s 是其父级的左子级）。这是下图所示的右案例的镜像。需要右旋父节点 p。 ………….. (ii) 右案例（s 是其父母的右孩子）。左旋父节点 p。

说明：本文限于篇幅，故而只展示部分的文档截图，完整的 Java面试学习文档小编已经帮你整理好了，有需要的朋友可私信“666”领取算法、树、Java等面试学习资料哦！

最后

写了好久终于写完了，最后总结一下。

红黑树和 AVL 树，一样，本质都是二叉查找树，两种树在保持平衡方面的能力不同，所以适合的场景也有所不同。同时，红黑树的应用比较广泛，值得一提的是，Java 8中HashMap的实现也因为用红黑树取代链表，性能有所提升。

红黑树的插入删除比较复杂，不容易理解，研究这块需要有耐心啊，哈哈。

文章中有什么有问题的地方，也欢迎指出。