深度强化学习论文中的阴影折线图——总结和分析
前言
作为目前人工智能算法的一个重要领域,强化学习算法的表现非常出色,然而,强化学习算法的结果是出了名的不稳定:超参数的搜索空间往往非常大,算法对不同超参数都较为敏感,且哪怕仅仅只有随机数种子的不同,算法的结果都可能出现不小的偏差。因此,当今主流的论文都会汇报多个随机数种子下,强化学习算法的平均表现。为了能将算法的表现与随机性同时展示在同一张图中,论文一般会使用带阴影区域的折线图来汇报训练过程中,reward等指标的变化情况。但是,在不同的文章中,画图的方法和阴影部分的含义都存在一定程度的不同,且许多文章并没有在文中说明自己阴影部分到底是什么含义,目前网上也找不到相关的分析和介绍。本文试图从具体的案例出发,讲清楚强化学习论文中经常出现的阴影折线图具体是什么含义,以及如何用Python代码去绘制这些图像。
一、经典论文中的实验结果图
首先介绍一下深度强化学习论文中,折线图常见的画法:
仅汇报多个实验的平均值,或仅做了一个实验
使用平均数和误差条来展示算法在不同随机数种子下的稳定性
折线使用中位数,阴影部分使用分位数
折线使用平均值,阴影部分使用标准差
折线使用平均值,阴影部分使用标准误差
折线使用平均值,阴影部分使用置信区间
……
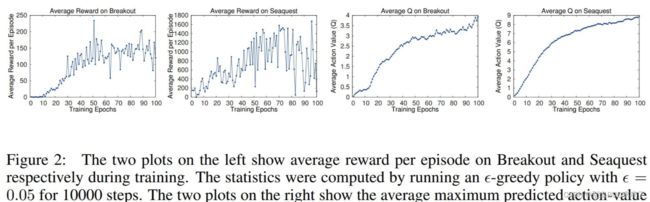
在早期的深度强化学习论文中,绘制折线图的方法各有不同。例如深度强化学习的开山之作:DQN的论文中,就没有绘制因随机数种子造成的误差,只汇报了实验结果:
在早期的深度强化学习论文中,绘制折线图的方法各有不同。例如深度强化学习的开山之作:DQN的论文中,就没有绘制因随机数种子造成的误差,只汇报了实验结果:
之后的文章尝试使用误差条(error bar)的形式来汇报实验结果,例如经典算法DPG和TRPO的实验部分:
还有一些算法,例如Double DQN的论文中,使用了带阴影区域的折线图来展示他们的实验结果。这篇文章中详细解释了他们图中阴影部分的含义:深色的折线是6次随机实验中分数的中位数(median),而阴影代表的是实验结果的最小值和最大值之间**,分位数(quantile)分别在10%和90%的位置**。这种画法和其他论文有较大的不同,这样画的一个特点就是,曲线上方和下方的误差距离可能是不相等的,因为分数是中位数,而不是极大值和极小值的平均数。

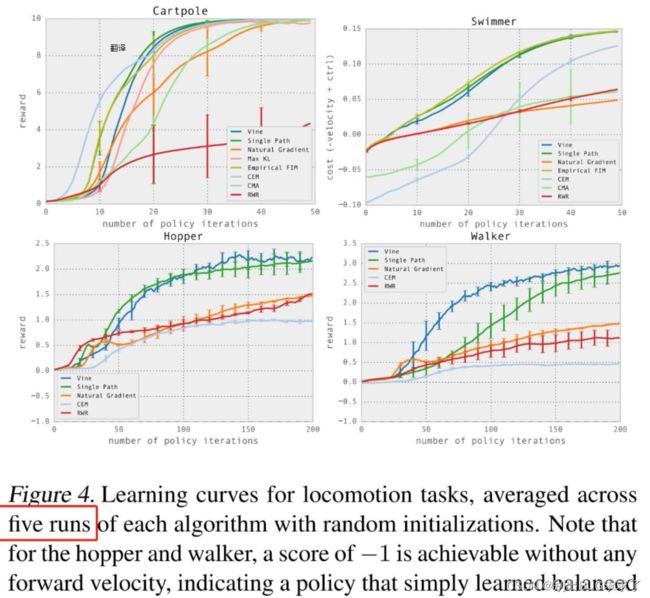
然后我们看一种比较经典的画法,这是一篇为连续控制空间的强化学习算法做benchmark的文章,同时提出了一个开源的框架,名为RLLab。这篇文章的图注中,明确的说明了他们图像的含义是平均值(mean)和标准差(standard deviation)。其中深色折线代表5个不同随机实验的平均值,而阴影部分上下分别代表正负标准差。这意味着,平均值的折线总是能纵向平分整个阴影部分。
还有一些画法,比如TD3的论文中,阴影部分代表的是标准差的一半,且他们用了10个随机数种子来进行实验。由于上下两篇文章使用的阴影部分含义不同,因此不能直接通过图比较两边的算法谁更稳定。
还有一些画法,例如阴影部分的含义是标准误差(standard error),或者95%的置信区间(confidence interval),在这里就不展示具体的例子了。
但比起刚刚举的例子,大多数文章根本没有解释阴影部分的含义,导致图的含义模糊不清。不过可能是由于阴影部分仅体现算法的稳定程度而非绝对指标,因此在强化学习的论文中,并没有被作为一个重点强调。但这也导致了,入门者在撰写强化学习论文时,常常会为这种含义不明、标准不定的折线图感到头痛,且对于标准差、标准误差、置信区间的计算方式也弄不太清楚,导致入门起来存在困难。一般而言,目前主流的论文还是以带阴影的折线图为主,因此文章接下来会一一介绍统计学中的基础知识,并讲解如何使用Python代码绘制阴影折线图。
二、标准差、标准误差、置信区间
为了绘制折线图,首先我们要知道如何计算实验结果中的标准差、标准误差和置信区间。这三者是不同的概念,但是常常会用同样的方法进行绘制,因而常常会导致混淆。文章接下来会介绍这三个概念,感兴趣的读者可以深入阅读以下文章:David L Streiner. Maintaining Standards: Differences between the Standard Deviation and Standard Error, and When to Use Each. 1996.
- 标准差 Standard Deviation
标准差(或标准偏差)刻画了一组数据的离散程度,是方差的算术平方根,也是概率统计中最常使用的统计量之一。对于一组平均数为 ,数据个数为 的离散数据,其总体标准差的公式为:
如果总体服从某个分布,则只能通过抽样的方式通过样本标准差来估计总体的标准差。若从分布中抽样出 个样本,这些样本的均值为 ,则样本标准差为:
此时计算出的样本标准差是总体标准差的无偏估计。
- 标准误差 Standard Error
标准误差是标准差与样本数量算术平方根的商,其计算公式为:
标准差是属于总体的统计量,刻画的是数据总体的离散程度,而标准误差刻画的是采样过程中,数据均值的波动情况。随着采样的次数增大,标准误差将越来越小,最终趋于0。在有限次采样的实验中,标准误差可以很好地用于衡量均值的准确程度,与标准差是不同的概念。
- 置信区间 Confidence Inverval
置信区间的含义,和分布中的“样本有多少概率落在某个范围内”是不同的两个概念!假设所有中学生的身高服从正态分布: ,我们通过采样得到了样本的均值 和标准偏差 ,考虑以下两个说法:
所有中学生的身高均值有95%的概率在某个范围内;
有95%的中学生身高范围在某个范围内。
这两个概念很容易混淆,尤其是在总体本身就服从正态分布时,更容易弄错。
置信区间的值,与所使用的统计学检验方法有关(如U检验,又叫z检验,以及t检验);
样本有多少概率落在某个范围内,与总体的分布形式有关(如正态分布、卡方分布等)。
一般而言,当样本数量较大(如 )时我们可以使用U检验(又叫z检验)来对我们的估计值进行检验。此时检验所使用的分布为正态分布,均值为 ,标准差为 。可以通过查询正态分布表得知,样本的真实均值 有95%的概率落在 内。当样本数量较小时,一般使用t检验来进行统计学检验。t检验的分布形式和正态分布相似,但是具体的分布形状与样本数量(自由度)有关。
总而言之,论文中阴影部分所表示的90%或95%置信区间,是根据标准误差所计算出的区间,当随机实验的次数增加时,阴影部分会变小。
- 应该使用什么图?
因为很多论文并没有解释他们的阴影部分的含义,因此很难说目前主流的画法中,阴影部分到底代表了什么。甚至有可能,许多作者也没有弄清楚标准差、标准误差和置信区间的关系。
所幸,OpenAI开源了一套绘制阴影折线图的代码,集成于openai/baselines仓库中。这套代码中给出了两种画法,分别使用标准差和标准误差作为阴影部分,由参数shaded_err和shaded_std控制。相信目前主流的强化学习论文,也参考了这套代码的实现方式,接下来我们将以baselines中的代码为例,详细讲解如何绘制论文中的阴影折线图。
三、从baselines学习绘图
- baselines给出的解决方案
baselines这套代码缺乏文档,唯一的文档居然是在Colab中教你如何画图。一般而言,强化学习的实验结果曲线并不平整,存在大量的噪声干扰因素,如果原原本本的画下来,效果大概就会如下图所示:
原始的实验数据
为了使得实验结果更好看,需要对图像进行平滑(smooth)操作。最简单的方法就是和数据点附近的数据一起取个平均值,就能够使得曲线的可读性大大增加。
平滑后的曲线
这种简单的平滑方式给数据点邻域内的每个值赋予了相同的权重,然而训练过程应当是时序的,应当对当前时刻的数据赋予更大的权重。此外,在强化学习实验中,我们往往会在相同的setting下,使用不同的随机数种子开展多个实验,这些实验的横轴(timesteps)可能无法对齐,例如第1组实验的横轴是[0, 1001, 2002, 3003],第二组实验的横轴是[500,1501,2503],这种不对齐会导致无法计算出某个时刻下所有实验的标准差,导致无法绘制出阴影折线图。
为了解决以上两个问题,baseline中给出了一种基于指数移动平均(exponential moving average, EMA)和重采样(resample)的数据处理方式,使用指数移动平均实现更科学的平滑方式,并使用重采样将不同实验的横轴对齐。
- 指数移动平均 Exponential Moving Average
指数移动平均(EMA)是一种很常用的平滑方式,不仅用于折线图,甚至可以用于模型参数的更新,在金融领域、深度学习中都有广泛的运用。常用的Tensorboard就内置了指数移动平均的功能,用于自动平滑曲线。
EMA的计算公式如下:
其中 为 时刻的移动平均值, 为 时刻的真实值, 为权重因子。上述公式为递推公式,若将上述公式转化为只和 相关的形式,则:
这种方法显然存在问题,例如当 的时候, ,只有当 变大时,移动平均值才会接近真实值。为了解决该问题,引入一项偏差修正项,修正后的指数移动平均公式为:
当 大而 小时,由于 ,系数 会变得很小,接近于0,以至于无法对 产生影响。关于 到底多大才算没有影响,我们一般定义 为有效权重项的阈值。
在baselines的代码中,使用变量decay_steps来表示有效权重项的范围,其与系数beta的关系是beta = np.exp(-1 / decay_steps)。举例,若decay_steps = 5,则只有距离当前时刻 在5个时刻以内的值才会被看做有效值,而5个时刻以外的值被看做无效值,此时满足 。
- 重采样
在baselines中,重采样是基于指数移动平均实现的。代码首先读取所有实验的数据,将数据中横轴的最大值和最小值提取出来,分别定为high和low。然后,代码将high和low之间的区间分为n-1个均匀的间隔,定义这个间隔为 ,算上头和尾,共有n个时间点可以采样。我们把这些时间点分别称为
重采样的问题在于,如何计算每组实验数据在 时刻的值呢?如果刚好这组实验数据在 处有值,则直接赋值即可。如果这组实验数据在 处没有值,但是在 之间的某个时刻有值,应当如何估算出 处的值呢?
baselines给出了如下的解决方案:
这个式子沿用的其实就是指数移动平均的思想。刚刚我们探讨的指数移动平均的递推公式中, 是离散的,只有 和 的关系。那么, 的值可不可以是小数呢?当然可以,且结论同样适用。这里就是通过指数移动平均的思想,使用位于 之间的点,计算出了 的值。如果这个区间内没有点,则 ,指数移动平均时,就只能完全根据 时刻之前的点来预测 时刻的值 了。
- baseline绘图代码的流程
读取数据,得到不同随机数种子下的实验曲线,横轴为时间片,纵轴为度量指标(如reward);
对每组数据使用上面介绍的方式进行重采样,将所有值映射到low到high之间的n个均匀的时间点上;
对这n个均匀的时间点的数据分别进行指数移动平均,得到平滑后的曲线;
把原始数据的横轴取负值,重新进行2~3两步。因为指数移动平均只能利用单边(即当前时刻之前)的数据进行移动平均,但我们希望当前时刻之后的数据也可以用于移动平均。这一步在代码中被称之为symmetric_ema。
对正向和反向的两次指数移动平均的结果取均值,作为当前实验曲线用于画图的值。
计算出n个均匀的时间点下,每个时间点数据的均值、标准差和标准误差。根据设置来决定是绘制标准差阴影还是标准误差阴影。画阴影可以使用matplotlib的fill_between()函数来实现。
总结
这篇文章详细介绍了深度强化学习中,阴影折线图的含义和画法。希望大家能在看完文章的介绍之后,能够自己写出绘制阴影折线图的代码。如果有错误或疏漏之处,欢迎大家在评论区指出交流。