LeetCode刷题总结C++-数组篇（中）

LeetCode刷题总结C++-数组篇（中）

    本文接着上一篇文章《LeetCode刷题总结C++-数组篇(上)》，继续讲第二个常考问题：矩阵问题。

    矩阵也可以称为二维数组。在LeetCode相关习题中，作者总结的考点有：矩阵元素的遍历、矩阵位置的旋转、矩阵行或列次序的交换、空间复杂度为O(1)等。本期共12道题，2道简单题，8道中等题，2道困难题。

• 例1是杨辉三角的一个延申题，是一道非常经典的矩阵习题，本题理想解法是动态规划，但是也可以采用递归来求解。
• 例2是一道顺时针访问矩阵元素的习题，在不少面试题中有见到。
• 例3、例4和例5则强调如何利用矩阵本身的空间，来变换矩阵中的元素，即空间复杂度为O(1)。用到了元素间交换和位运算策略，其中相关解法很巧妙。
• 例6是一道如何移动矩阵的问题。
• 例7和例8则是考察我们快速理解题意，并在较短时间内完成较高质量代码的能力。即编写的代码争取一次性通过。
• 例9考察我们如何把二分查找的应用场景由一维数组转换到二维数组。
• 例10是一道动态规划结合矩阵的经典习题，并且还可以延申出求最短路径的问题。
• 例11则很有意思，该题是上篇例6中《和为K的子数组》的一个升级版，把一维数组的场景变换成了二维的场景，并结合了动态思想，因此题目难度由中等变成了困难。
• 例12是一道困难级别的习题，该题主要考察我们的数学分析能力，如何灵活变换矩阵的行和列，以及细节的处理能力。

 

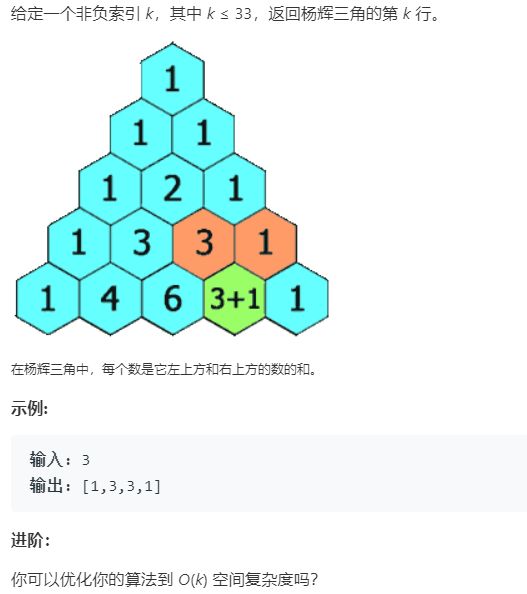
例1 杨辉三角 II

题号：119，难度：简单（可参考 杨辉三角，题号：118，难度：简单）

题目描述：

 

解题思路：

依据杨辉三角的规律，当前行的数据和上一行的数据有着递推关系：dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。依据该递推公式可以写一个较为清晰的动态规划解法，其空间复杂度为O(k)。但是，也可以采用递归的思想来解决。此处提供一个应用递归思想来解决该问题的代码。

具体代码：

class Solution {
public:
    vector getRow(int rowIndex) {
        vector kRows(rowIndex + 1); // 第K行的vector大小为 rowIndex+1
        for (int i = 0; i <= rowIndex; ++i) {// 利用前一行求后一行，第K行要循环K遍
            kRows[i] = 1; // 行末尾为1
            for (int j = i; j > 1; --j) {// 每一行的更新过程,从尾部开始修改
                    kRows[j - 1] = kRows[j - 2] + kRows[j - 1];
                }
        }
        return kRows;   
    }
};

 

执行结果：

 

 

例2 螺旋矩阵

题号：54，难度：中等

题目描述：

 

解题思路：

这题只需要不停的往内顺时针旋转访问即可。但是，在实现代码时需要注意边界的问题。另外，依据LeetCode上评论的解答思路，可以给访问过的元素做一个标记，或者统计当前已经访问的元素个数，这样更加有利于判断访问结束的时间节点。

具体代码：

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        vector  ans;
        if(matrix.empty()) return ans; //若数组为空，直接返回答案
        int u = 0; //赋值上下左右边界
        int d = matrix.size() - 1;
        int l = 0;
        int r = matrix[0].size() - 1;
        while(true)
        {
            for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
            if(++ u > d) break; //重新设定上边界，若上边界大于下边界，则遍历遍历完成，下同
            for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
            if(-- r < l) break; //重新设定有边界
            for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
            if(-- d < u) break; //重新设定下边界
            for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
            if(++ l > r) break; //重新设定左边界
        }
        return ans;
    }
};

 

 

执行结果：

 

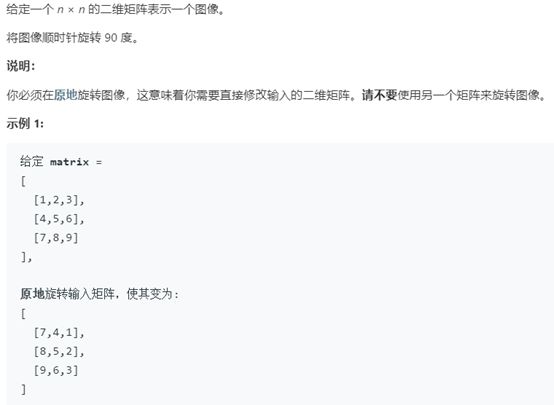
例3 旋转图像

题号：48，难度：中等

题目描述：

 

解题思路：

这题可以理解为是例2的一个演化版。题目意思说明为n*n的矩阵，所以不用考虑长方形矩阵的情形。下面代码给出的解答思路为依据正方形矩阵不停往内进行旋转转圈，每次转动的步数为边长长度减去1的大小，每往内旋转一步，正方形边长减2。

关键在于找到一个元素旋转后的下标和当前下标的关系规律

具体代码：

class Solution {
public:
    void rotate(vector>& matrix) {
        int n = matrix.size();
        for(int i = 0; i < (n >> 1); ++i){
            for(int j = i; j < n - 1 - i; ++j){
                swap(matrix[i][j], matrix[j][n - 1 - i]);
                swap(matrix[i][j], matrix[n - 1 - i][n - 1 - j]);
                swap(matrix[i][j], matrix[n - 1 - j][i]);
            }
        }
    }
};

// 逐层移动
class Solution {
public:
    void rotate(vector>& matrix) {
        int pos1=0,pos2=matrix.size()-1;
        int add,temp;
        while(pos1

 

执行结果：

 

例4 矩阵置零

题号：73，难度：中等

题目描述：

 

解题思路：

先说一下空间复杂度为O(m+n)的思路（PS：该思路不符合题意的原地算法要求）。申请两个一维数组，一个表示矩阵行，一个表示矩阵列。然后，遍历矩阵中所有元素，一旦出现零，把该零对应行和对应列的一维数组的值标记为常数1。最后，分别按行和按列给原始矩阵赋值零。

现在参考LeetCode上一个评论的思路，空间复杂度为O(2)。申请两个布尔变量cow和col，分别记录原矩阵第0行和第0列中是否存在零，如果存在标记为True，否则标记为False。然后，接下来的思路就是上面O(m+n)的解决思路，唯一不同的是此时的空间是采用原始矩阵的空间。

具体代码：

class Solution {
public:
    void setZeroes(vector>& matrix) {
        int n = matrix.size();
        if (n == 0) return ;
        int m = matrix[0].size();
        bool row0 = false, col0 = false;
        for (int i = 0; i < n; i++) { 
            for (int j = 0; j < m; j++) {
                if (matrix[i][j] == 0) {
                    if (i == 0) row0 = true;
                    if (j == 0) col0 = true;
                    matrix[0][j] = matrix[i][0] = 0;
                }
            }
        }
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if (matrix[0][j] == 0 || matrix[i][0] == 0) 
                    matrix[i][j] = 0;
            }
        }
        if (col0)
            for (int i = 0; i < n; i++) matrix[i][0] = 0;
        if (row0)
            for (int j = 0; j < m; j++) matrix[0][j] = 0;
    }
};

执行结果：

 

 

例5 生命游戏

题号：289，难度：中等

题目描述：

 

解题思路：

此题在要求采用原地算法，即不能应用额外的空间来更新原始的矩阵元素。此题的解决方案需要使用位运算来解决。

先观察题目对活细胞和死细胞的定义，然后把它们转化为二进制表示。

活细胞：1变换为二进制01，如果活细胞变为死细胞，只需要把01变为11，即1变为3，其最后一位依然可以识别为活细胞。

死细胞：0变换为二进制00，如果死细胞变为活细胞，只需要把00变为10，即0变为2，其最后一位依然可以识别为死细胞。

最后，采用board[i][j]&1进行位运算的法则来求取一个细胞周围的活细胞数量，并更新当前细胞的状态。

具体代码：

class Solution {
public:
    void gameOfLife(vector>& board) {
       // 01表示活细胞，01——>11变为死细胞，即由1变为3
       // 00表示死细胞，00——>10变为活细胞，即由0变为2
       int n = board.size();
       int m = board[0].size();
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                int count = countLive(board, i, j);
                if((board[i][j] & 1) == 1) {
                    if(count < 2 || count > 3) board[i][j] = 3;
                } else {
                    if(count == 3) board[i][j] = 2;
                }
            }
        }
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                if(board[i][j] == 3) board[i][j] = 0;
                if(board[i][j] == 2) board[i][j] = 1;
            }
        }
    }      
    int countLive(vector> board, int x, int y) {
        vector> step = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
        int count = 0;
        int n = board.size();
        int m = board[0].size();
        for (int i = 0; i < step.size(); i++) {
            int xNew = x + step[i][0];
            int yNew = y + step[i][1];
            if (xNew >= 0 && xNew < n && yNew >= 0 && yNew < m) {
                if ((board[xNew][yNew] & 1) == 1) {
                    count++;
                }    
            }
        }
        return count;
    }      
};


class Solution {
public:
    void gameOfLife(vector>& board) {
        int neighbors[3] = {0, 1, -1};

        int rows = board.size();
        int cols = board[0].size();

        // 创建复制数组 copyBoard
        vector >copyBoard(rows, vector(cols, 0));

        // 从原数组复制一份到 copyBoard 中
        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {
                copyBoard[row][col] = board[row][col];
            }
        }

        // 遍历面板每一个格子里的细胞
        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {

                // 对于每一个细胞统计其八个相邻位置里的活细胞数量
                int liveNeighbors = 0;

                for (int i = 0; i < 3; i++) {
                    for (int j = 0; j < 3; j++) {

                        if (!(neighbors[i] == 0 && neighbors[j] == 0)) {
                            int r = (row + neighbors[i]);
                            int c = (col + neighbors[j]);

                            // 查看相邻的细胞是否是活细胞
                            if ((r < rows && r >= 0) && (c < cols && c >= 0) && (copyBoard[r][c] == 1)) {
                                liveNeighbors += 1;
                            }
                        }
                    }
                }

                // 规则 1 或规则 3      
                if ((copyBoard[row][col] == 1) && (liveNeighbors < 2 || liveNeighbors > 3)) {
                    board[row][col] = 0;
                }
                // 规则 4
                if (copyBoard[row][col] == 0 && liveNeighbors == 3) {
                    board[row][col] = 1;
                }
            }
        }
    }
};

 

执行结果：

 

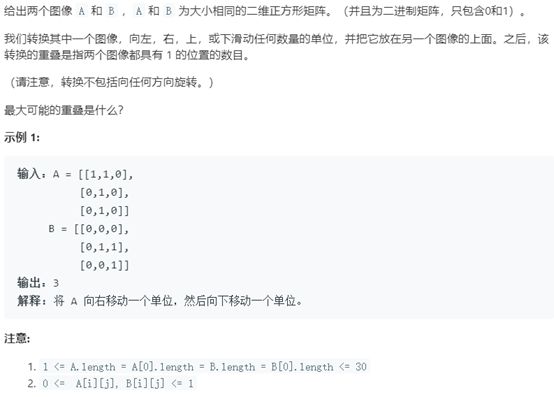
例6 图像重叠

题号：835，难度：中等

题目描述：

 

解题思路：

此题注意如何处理矩阵的移动，使得移动后两个矩阵进行匹配。直接采用两个for循环表示其中一个矩阵移动后的位置。具体变换形式参考代码。

具体代码：

class Solution {
public:
    int largestOverlap(vector>& A, vector>& B) {
        int result = 0, len = A.size();
        for(int i = 0; i < len; i++) {
            for(int j = 0; j < len; j++) {
                int count1 = 0, count2 = 0;
                for(int k = 0; k < len - i; k++) {
                    for(int l = 0; l< len - j; l++) {
                        count1 += (A[k][l] & B[k + i][l + j]);
                        count2 += (B[k][l] & A[k + i][l + j]);
                    }
                }
                result = max(result, count1);
                result = max(result, count2);
            }
        }
        return result;
    }
};

 

 

执行结果：

 

例7 车的可用捕获量

题号：999，难度：简单

题目描述：

 

解题思路：

本题较为简单，直接遍历矩阵找到车的位置，然后在车能行走的四个方向依次遍历即可。（放入此题的意图，题目比较长，读懂题意需要耗费一些时间，另外编写代码需要注意边界问题）

具体代码：

class Solution {
public:
    int numRookCaptures(vector>& board) { // 四个方向，只移动一次
        int cnt = 0, start = 0, end = 0;
        int dx[4] = {0, 1, 0, -1};
        int dy[4] = {1, 0, -1, 0};
        for (int i = 0; i < 8; ++i) {
            for (int j = 0; j < 8; ++j) {
                if (board[i][j] == 'R') {
                    start = i;
                    end = j;
                    break;
                }
            }
        }
        for (int i = 0; i < 4; ++i) {
            for (int step = 0;; ++step) {
                int tx = start + step * dx[i];
                int ty = end + step * dy[i];
                if (tx < 0 || tx >= 8 || ty < 0 || ty >= 8 || board[tx][ty] == 'B') break;
                if (board[tx][ty] == 'p') {
                    cnt++;
                    break;
                }
            }
        }
        return cnt;
    }
};

 

执行结果：

 

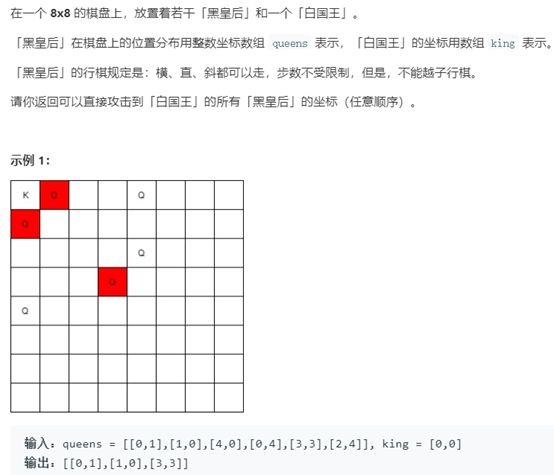
例8 可以攻击国王的皇后

题号：1222，难度：中等

题目描述：

 

解题思路：

以国王为起点往八个方向迭代，循环结束条件为出界((x < 0 || x >= 8) || (y < 0 || y >= 8))或者在这个方向上找到第一个皇后，那么结束当前这个循环，继续迭代下一个方向。

具体代码：

class Solution {
public:
    vector> queensAttacktheKing(vector>& queens, vector& king) {
        vector> res;
        //标志数组
        vector> grid(8, vector(8, 0));
        for(vector queen : queens) {
            grid[queen[0]][queen[1]] = 1;
        }
        //8个方向  右--左--上--下--右上--右下--左上--左下   
        vector dx = {-1, -1, -1, 0, 1, 1, 1, 0};
        vector dy = {-1,  0,  1, 1, 1, 0,-1,-1};
        //从第一个方向开始到第八个方向
        for(int i = 0; i < 8; i++) {
            int x = king[0] + dx[i] ;
            int y = king[1] + dy[i] ;
            //起始位置为king的坐标,找到第一个皇后停止这个方向的查找，或者直到出界
            while ( x >= 0 && x < 8 && y >= 0 && y < 8) {
                if(grid[x][y]){
                    res.push_back({x,y});
                    break;
                }
                x += dx[i];
                y += dy[i];
            }
        }
        return res;
    }
};

 

 

执行结果：

 

例9 搜索二维矩阵

题号：74，难度：中等

题目描述：

 

解题思路：

正常的想法是把矩阵想象成一个一维数组，然后采用二分查找的思路来实现。但是，这种方法可能需要处理（1，m）和（m，1）这两种特殊的二维矩阵边界问题（PS：在LeetCode上看到过直接应用二分查找很快解决的代码）。因为矩阵按照行是有序的，不妨采用每行最后一个值作为边界与目标值进行比较大小，每次增加一行或者减少一列的数据，具体实现可参考代码。

具体代码：

class Solution {
public:
    bool searchMatrix1(vector> matrix, int target) { // 二分查找的代码
        if (matrix.size() == 0 || matrix[0].size() == 0)
            return false;
        int begin, mid, end;
        begin = mid = 0;
        int len1 = matrix.size(), len2 = matrix[0].size();
        end = len1 * len2 - 1;
        while (begin < end) {
            mid = (begin + end) / 2;
            if (matrix[mid / len2][mid % len2] < target)
                begin = mid + 1;
            else
                end = mid;
        }
        return matrix[begin / len2][begin % len2] == target;
    }
    bool searchMatrix(vector>& matrix, int target) {
        if (matrix.size() == 0) return false;
        int n = matrix.size(), m = matrix[0].size();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (matrix[i][j] == target) {
                    return true;
                }
            }                            
        }
        return false;
    }
};

 

执行结果：

 

 

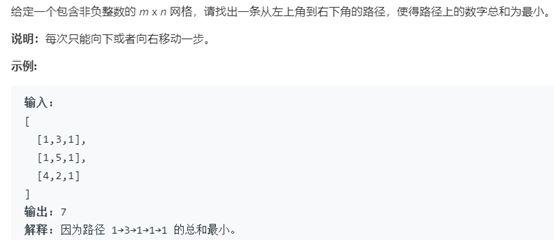
例10 最小路径和

题号：64，难度：中等

题目描述：

 

解题思路：

此题最直接的思路是采用递归进行深度搜索遍历来解决，但是提交代码后发现会出现超时的问题。此时，需要考虑应用动态规划的思想来解题。动态规划的转换方程：dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]，另外需要考虑矩阵边界的问题。

具体代码：

class Solution {
public:
    int minPathSum(vector>& grid) {
        if (grid.size() == 0 || grid[0].size() == 0) {
            return 0;
        }
        int rows = grid.size(), cols = grid[0].size();
        auto dp = vector < vector  > (rows, vector  (cols));
        dp[0][0] = grid[0][0];
        for (int i = 1; i < rows; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < cols; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < rows; i++) {
            for (int j = 1; j < cols; j++) {
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[rows - 1][cols - 1];
    }
};

 

执行结果：

 

例11 元素和为目标值的子矩阵数量

题号：1074，难度：困难

题目描述：

 

解题思路：

这道题其实是《和为K的子数组，题号：560，难度：中等》的一个升级版，560题是一维数组，本题是二维数组，其和变成了一个子矩阵的形式。此处我们可以采用把矩阵每行的元素变换成从该行开始道当前元素的和，另外单独选两列求矩阵和，这样就把二维数组变成了列形式的一维数组求和。此时，解题思路就和560题一样。

具体代码：

class Solution {
public:
    int numSubmatrixSumTarget(vector>& matrix, int target) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int R = matrix.size();
        int C = matrix[0].size();
        vector > sums(R + 1, vector(C + 1, 0));
        for (int i = 0; i < R; ++i) {
            for (int j = 0; j < C; ++j) {
                sums[i + 1][j + 1] = matrix[i][j] + sums[i + 1][j] + sums[i][j + 1] - sums[i][j];
            }
        }
        int res = 0;
        for (int i = 0; i < R; ++i) {
            for (int j = i; j < R; ++j) {
                unordered_map m{{0, 1}};
                for (int k = 0; k < C; ++k) {
                    int s = sums[j + 1][k + 1] - sums[i][k + 1];
                    if (m.count(s - target)) {
                        res += m[s - target];
                    }
                    ++m[s];
                }
            }
        }
        return res;
    }
};

 

执行结果：

 

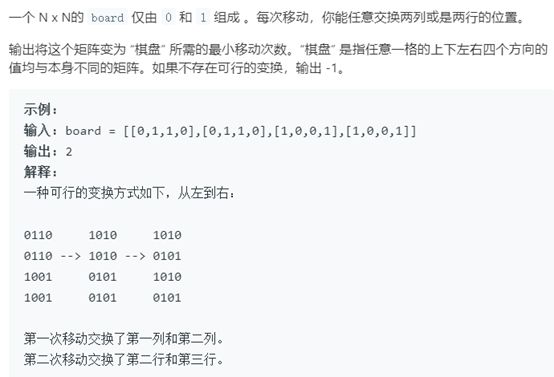
例12 变为棋盘

题号：782，难度：困难

题目描述：

 

解题思路：

本题分析一下01出现的规律，可知如果n为偶数，那么每行每列中0和1的个数必然相等；如果n为奇数，那么0和1个数差的绝对值为1。由于矩阵只能交换行和列，结果要出现0和1不断相间排列，那么所有行中只能出现两种模式的01排列方式，并且这两种排列方式互补。例如，n=4, 第一行排序：1001，那么其他行要不等于1001，要么等于0110，否则就不可能转换为棋盘，直接输出-1即可。对于列的情况，和行一样。（PS：此题需要处理最小变换次数的边界问题，分奇偶讨论行或者列的最小交换次数）

具体代码：

class Solution {
public: 
    int movesToChessboard(vector>& board) {
        int n = board.size();
        int m = board[0].size();
        if(check(board)) {
            int row = 0, start = board[0][0];
            for(int i = 1;i < n;i++) {
                if(board[i][0] == start) row++;
                start = 1 - start;
            }
            int col = 0; 
            start = board[0][0];
            for(int j = 1;j < m;j++) {
                if(board[0][j] == start) col++;
                start = 1 - start;
            }
            if (n % 2 == 0) { // 分奇数偶数讨论行和列最小交换次数
                row = min(n-row, row);
                col = min(n-col, col);
            } else {
                if(row % 2 == 1) row = n-row;
                if(col % 2 == 1) col =  n-col;
            }
            return row / 2 + col / 2;
        }
        return -1;
    }
    
    bool judgeEqual(vector>& board, int i, int j) {
        int n = board.size();
        int m = board[0].size();
        for(int k = 0; k < m; k++) {
            if(board[i][k] != board[j][k]) return false;
        }
        return true;
    }
    
    bool judgeNotEqual(vector>& board, int i, int j) {
        int n = board.size();
        int m = board[0].size();
        for(int k = 0;k < m;k++) {
            if(board[i][k] == board[j][k]) return false;
        }
        return true;
    }
     
    bool check(vector>& board) {
        int n = board.size();
        int m = board[0].size();
        int row_0 = 0, row_1 = 0, col_0 = 0, col_1 = 0;
        for(int i = 0;i < m;i++) {
            if(board[0][i] == 0)
                row_0++;
            else if(board[0][i] == 1)
                row_1++;
            if(board[i][0] == 0)
                col_0++;
            else if(board[i][0] == 1)
                col_1++;
        }
        if(abs(row_0 - row_1) > 1 || row_0+row_1 != m) return false;
        if(abs(col_0 - col_1) > 1 || col_0+col_1 != n) return false;
        row_0 = 0;
        row_1 = 0;
        for (int j = 1;j < m; j++) {
            if (judgeEqual(board, 0, j)) {
                row_0++;
            } else if (judgeNotEqual(board, 0, j)) {
                row_1++;
            }
            else {
                return false;
            }
        }
        return true;
    }
};

 

 

执行结果：