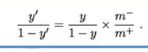机器学习经典方法思想

本文附带问题以及答案，and总结，在每个章节对应的末尾

目录

 1 绪论

2 模型评估和选择

留出法(ps:留一法是只留一个验证)

交叉验证法(k折交叉验证)(10折交叉验证)

自助法

调参和最终模型

 性能度量

查准率、查全率

P-R曲线和平衡点F1

ROC曲线和AUC面积、Lrank排序损失

代价敏感曲线(代价曲线)

问题和总结

3 线性模型

线性回归

 对数几率回归：对数几率函数Sigmoid

 线性判别分析LDA

多分类学习

类别不平衡问题(样本分布不均匀)

 类别不平衡的处理：

 梯度下降法

问题和总结

4 决策树

基本流程(算法)

信息熵和信息增益

信息增益Gain(D,某属性a)：ID3算法

增益率Gain_ratio(D,某属性a)：C4.5算法

基尼值Gini，基尼指数Gini_index：CART算法

预剪枝：生成决策树的过程中剪枝

后剪枝：生成决策树之后剪枝

连续值：可取连续值的属性

缺失值：某些数据的其中某个数据缺失，若全部弃用则会很浪费

多变量决策树：用线性关系替代多个变量

问题和总结

 过拟合

5 神经网络

BP算法（误差逆传播）

全局最小、局部最小

问题和总结

6 支持向量机SVM

SVM基本原理

 SMO算法的基本思路：

 核函数：升维，使得样本在高纬度线性可分(可以被超平面隔开)

软间隔和正则化

支持向量回归SVR

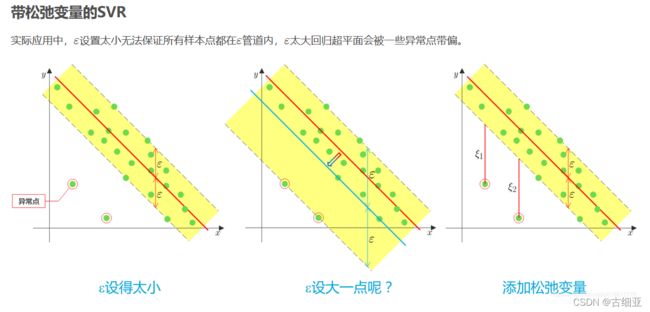
带松弛变量的SVR

 问题和总结

7 贝叶斯分类器

 朴素贝叶斯分类器(NB算法)

拉普拉斯平滑(拉普拉斯修正)：

 朴素贝叶斯优缺点

半朴素贝叶斯分类器

贝叶斯网络

8 集成学习

个体与集成

集成学习的效果

Boosting：个体学习器之间有强依赖关系

AdaBoost算法

 样本权重≠分类器权重

Bagging：个体学习器之间相互独立

Boosting和Bagging的区别

随机森林RF：Bagging的一个扩展变体（随机属性选择）

 结合策略：平均法、投票法、学习法

问题和总结

---

 1 绪论

​​

2 模型评估和选择

留出法(ps:留一法是只留一个验证)

大部分样本作训练集S，剩下的作验证集T。

S、T的选取需满足分层抽样，避免其他因素干扰，保持数据分布一致性

训练集：验证集是几比几(如七三分，八二分)分实际情况考虑决定

单次留出法得到的估计结果不够可靠，通常会多次随即划分且多次实验，取结果平均值

交叉验证法(k折交叉验证)(10折交叉验证)

类似于留出法，但把样本划分为k个，抽取k-1个作为训练集S，剩下的1个作为测试集T

一共进行k次，取不同的组合，将平均值作为结果

k通常取10，因此也叫10折交叉验证。也可以取5，20​​

缺点：步骤繁琐，数据量大时，对算力要求较高。

自助法

例如有10个数组1~10，从中可放回的拿10次，放入新的集合S，那么有个别数字始终不会被拿起，这部分数字放入新的集合T

​​

 适用于：数据量小 or 难以划分的

缺点：改变初始数据集分布，会引入估计偏差(例如2这个数字在初始集合只有一个，但在S中有2个或者3个)

谨慎使用！

调参和最终模型

假设一个算法有3个参数，分别可以取5个候选值，那么对于每一组“训练集、测试集”就有5³=125个模型需要考察

候选值的选取需要权衡考虑“算力”和“性能”

调参步骤：训练集+测试集+参数配置1——>训练集+测试集+参数配置2——>训练集+测试集+参数配置3——>训练集+测试集+参数配置4——>...............——>最后实际使用时用验证集验证

 性能度量

​​

​​

// 双杠写错了，是01损失函数

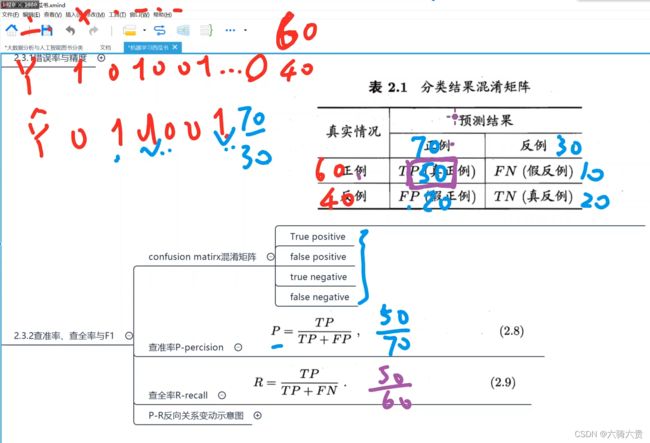
查准率、查全率

查准率 P = 实际预测正确的 / 预测的正例个数

查全率 R= 实际预测正确的 / 所有的实际正例

下方：Accuracy——>精度 

Precision——>查准率P：描述准确程度，样本不均衡时，查准率没有什么意义

Recall——>查全率R：描述预测到的正例覆盖程度

​​

​​

通常取平衡点P=R直线决定的点来衡量一个模型的好坏(P=R时的值)

在不同情况对P和R的要求不同，推荐算法中P更重要，逃犯追查系统中R更重要

P-R曲线和平衡点F1

平衡点：BEP，此点P=R

F1：P和R的调和平均数

​​

ROC曲线和AUC面积、Lrank排序损失

ROC曲线所处的坐标中，横轴为FPR，数值越大准确率(Accuracy)越低。纵轴为TPR，数值越大准确率越高，因此可以出现FPR，TPR都很大，但Accuracy很低的情况

我们希望TPR(真正例率)变大的同时，FPR(假正例率)增长的缓慢，那么曲线就像蓝色曲线一样的弯曲最好。而TPR变大的同时FPR不可避免的会变大，因此曲线只能是这样​​

 AUC就是ROC包围的面积，面积越大，该模型的性能越好。

损失Lrank=1-AUC

​​

代价敏感曲线(代价曲线)

//为什么引入代价敏感曲线

“代价敏感错误率”：不同的方向误判代价不同(eg：漏诊比误诊更严重)，因此需要加权。

​​

 代价敏感曲线:由ROC曲线中的坐标确定代价曲线中的FNR，从而绘制出代价曲线（共同下界）

阴影面积即为：期望总体代价

​​

​​

问题和总结

​​

 ​​

​​

3 线性模型

该章节下最重要的是梯度下降法

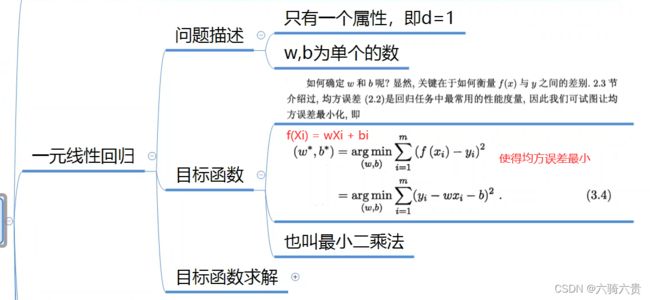
线性回归

回归问题可以映射到分类问题，是神经网络的基础

​​

​​

 E在这里是均方误差，让w和b的偏导等于0，求得w和b的最优解。该求解均方误差E最小化的过程叫“线性回归模型的最小二乘‘参数估计’”

以下为多元情况：求的是由协方差矩阵决定的最优解

​​

 以下为广义线性回归：

​​

 本质也是线性回归问题，只是进行了y的函数映射

 对数几率回归：对数几率函数Sigmoid

对数几率函数Sigmoid在横轴为0时会有连续的突变，形状接近阶跃函数，所以可以用于分类学习

虽然名字是“回归”，但实际上是一种分类学习的方法。由于在某一点会有突变，预测值高于这个阈值(突变点横轴) or 低于这个阈值，都会判定为不同的分组

​​

 这里的z可以换成多元情形：Z = A(X)T + b

 ​​

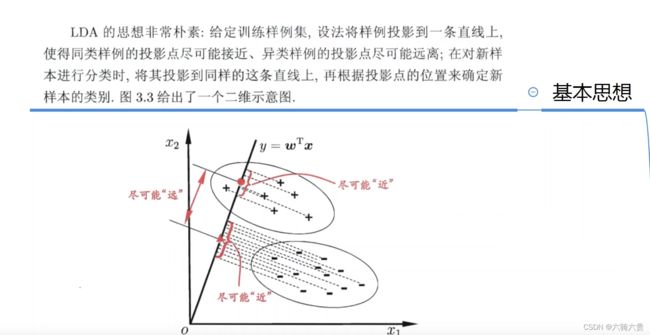
 线性判别分析LDA

此章性价比很低，该方法虽然朴素，但并不简单

​​

 目的：让同类别的点之间方差最小，不同类别的方差最大

原理：通过投影放大不同组的点之间的差距

注意区别于后面的：SVM核函数

多分类学习

该方法在实战中可用深度学习的方法替代，可用性不高，但简单总结

将多分类任务拆解为多个二分类任务求解，典型的有3种策略：

1，一对一   OvO

2，一对其余OvR

3，多对多   MvM

ECOC：纠错输出码：将编码的思想引入类别拆分

类别不平衡问题(样本分布不均匀)

样本中训练样例的正反例的数目相差无几时，影响不大；但如果某一种较大，则会产生很大的影响，例如1000个样本有999个正例，1个反例，那么一个只会返回正例的学习器的精度一定是99%，这种学习器没有任何意义

类别不平衡造成的原因：

1. OvR MvM分类策略导致的不平衡
2. 采样本身几乎不可能无偏

​​

 类别不平衡的处理：

1. 欠采样：用EasyEnsemble算法，将反例划分为多个集合供机器学习，从全局来看不会丢失信息。也可简单删除一些不重要的样本
2. 过采样：增加一些样本采集，但不能重复采用，否则会导致过拟合
3. 阈值移动：仍用原始数据集训练，只是最后进行缩放m+/m-​​

 梯度下降法

思想和《最优化方法》中的最速下降法高度相似

都是沿着“负梯度”方向进行迭代

梯度下降算法原理讲解——机器学习_Arrow and Bullet-CSDN博客_梯度下降法

问题和总结

​​

​​

 ​​

4 决策树

基本流程(算法)

1. 根节点出发，将根节点的样本集合D作为第一个节点，引出分支节点
2. 第一个分支节点按具体计算结果，从样本的属性集中选一个再分支
3. 划分选择的方法：Gain Gain_ratio Gini算法

举例(看完整个后反回来看例子)：

有样本集D记录了西瓜的各属性和好坏

决定第一个分支选什么属性：计算每个属性基于D的信息增益Gain，或增益率Gain_ratio，或基尼指数Gini

决定第  i 个分支选什么属性：计算每个属性基于i-1的信息增益Gain，或增益率Gain_ratio，或基尼指数Gini

Gain Gain_ratio取最高，Gini取最低​​

信息熵和信息增益

信息：例如给一个样本集D，一共17个样本，其中每个样本都有{色泽、根蒂、敲声、纹理、脐部、触感}6种属性，并且样本集中有8个好瓜，9个坏瓜。   这些已知的东西都叫信息，但信息不是越多越好，其中有些假信息称作“噪声”。

噪声：噪声会导致过拟合。

数据：信息＋噪声，样本集D中的只能叫数据

信息熵Ent(D)：通俗讲就是描述信息的混乱程度，Ent和属性有多少个无关，它由结果分类情况决定，显然是Ent(D)越小，D的纯度越高；   既然是描述混乱程度，那么样本集D的信息熵就由该样本的分类情况决定，例如：抛1个硬币，结果有2种；抛3个硬币，结果有8种；判断西瓜是不是好瓜，结果有2种；信息熵的计算公式和计算举例如下：

​​

​​

 另外，如果是选中“纹理”作为节点，计算Ent(D1)，那么就要以纹理的结果集{清晰、模糊、稍糊}进行计算(以log2为底，一共3项加和 再取负)

信息增益Gain(D,某属性a)：ID3算法

表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。可以很好的判断各个特征划分数据集的能力。故越大越好

        如果说Ent信息熵用来描述该节点 D 的混乱程度，那么信息增益Gain就是评判“在已分支的此节点上，再细分下一个属性分支的增益效果”；此增益效果表达的是：如果下一个节点来判断xx属性，对整个模型的增益效果如何

        例如：在“纹理”分支之下，究竟该选择哪个属性来进行下一步判断呢？即选Gain最大的属性

        然而，有些属性的可选值很多，造成了生成的决策树有很多分支都是它的，这也是单纯用信息增益Gain的缺点：对可选值多的属性有偏好

增益率Gain_ratio(D,某属性a)：C4.5算法

        用Gain(D,a)除以一个对应的系数IV(a)，消除“对可选值多的属性的偏好”；但这也导致该方法对可选值少的属性有偏好

        使用时先用普通的信息增益Gain方法选出超过平均值的前几名，然后再在这前几名中用增益率Gain_ratio来选出最佳的分支，既保证了纯度，也降低了计算量        

​​

基尼值Gini，基尼指数Gini_index：CART算法

与前面两种方法的基本思想一致，不过是选择基尼指数最小的

​​

决策树算法原理(CART分类树) - 做梦当财神 - 博客园

预剪枝：生成决策树的过程中剪枝

            基于“贪心”本质，能剪则剪。

         如果某个分支的存在并没有提高准确率，or降低了准确率，则剪掉

1. 降低了过拟合风险；
2. 显著减少了决策树训练时间；
3. 但带来了欠拟合的风险

后剪枝：生成决策树之后剪枝

        能不剪，则不剪，剪前后若准确率相等，则保留

1. 同样的训练模型，后剪枝的决策树保留了更多的分支
2. 后剪枝的欠拟合风险很小
3. 泛化性能往往优于预剪枝(分的更细，在面对陌生数据时判断更准确)
4. 训练时间长的多(生成决策树之后需要自底向上逐一考察，计算开销大)

“在有噪声的情况下，剪枝操作甚至能将泛化性能提高25%”

连续值：可取连续值的属性

        例如：脐部{凹陷，平坦，稍凹}这种是离散值；而密度，xx含量等很多属性值都是连续的

        因此在划分分支的时候，需要有一个间断点

1. 间断点的划分方法：二分法，例如有17个排序后的点集，两两之间算中位数，一共算16次，生成16个t值，组成一个t的集合T，用T中的划分点代入Gain算法，计算Gain(D，该属性，t为划分点)，取Gain最大值，对应的t即为最终确定的划分点
2. 划分完t之后，如果子分支还需用到更细的判断， 可以使用t的子集：例如：一个节点判断“密度<=0.381”那么后续的子节点可以使用任何"密度<0.381"范围的判断依据

缺失值：某些数据的其中某个数据缺失，若全部弃用则会很浪费

        属性a缺失值处理方法：

1. 西瓜书上p88：跳过该属性a的判断，直接判断下一节点的所有可能性，但需要加上训练集中的比例权重
2. (离散值)：众数填充、相关性最高的列(属性b总是与属性a的取值几乎一一对应)填充
3. (连续值)：中位数、相关性最高的列(同上)做线性回归估计

多变量决策树：用线性关系替代多个变量

        有些属性之间有一定的线性关系，例如：密度和含糖量之间存在着线性关系，那么就把密度和含糖量分别乘上各自的权重系数，用他俩组成的一个式子<=t 或 >=t 作为分界点来判断

多变量决策树算法：贪心寻找每个属性的最优权值，线性分类器的最小二乘法

问题和总结

分类和回归的区别
什么是损失函数

​​

 ​​

​​

​​

 ​​

 过拟合

过拟合 欠拟合的原因and解决

链接2

​​

​​

5 神经网络

最基本成分：神经元模型 M-P神经元模型

        M-P神经元模型：在这个模型中，神经元接受到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元将接收到的信号与阈值对比，如果大于这个阈值，则经过激活函数(Sigmoid函数，连续的阶跃函数)​​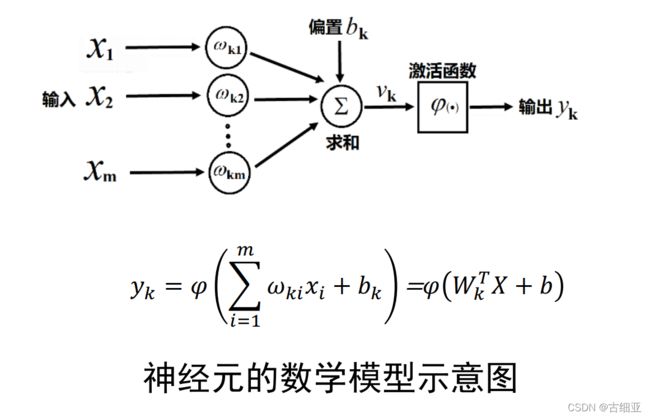

 Xi是输入信号，Wi是来自第i个神经元的连接权重

 感知机、多层网络

感知机由两个神经元组成（类似突触结构）

给定训练数据集，权重Wi和阈值θ都可以通过学习得到​​

 学习率不能一成不变，学习率也叫搜索步长，如果过大，在接近最优解的附近会发生震荡，如果过小，搜索的速率会很慢

BP算法（误差逆传播）

1. 多层网络的学习能力>>远大于>>单层感知机
2. 一般说的BP网络就是用BP算法训练的多层前馈神经网络
3. BP算法是迄今为止最成功的神经网络学习算法
4. BP算法基于梯度下降法

全局最小、局部最小

基于梯度的搜索是使用最为广泛的最优化方法，但每当达到梯度为0的时候，不能判断此处为局部最小还是全局最小，因此在现实中，常采用以下方法“跳出”局部最小

1. 随机梯度下降法
2. 从不同的初始点开始搜索
3. 模拟退火技术

其他常见的神经网络

BP神经网络、RBF网络、ART网络、SOM网络、Elman网络、Boltzmann机

常用神经网络的分类 - Siucaan - 博客园

深度学习（deep learning）

参数多、容量大，能完成更复杂的学习任务；在以往，复杂的模型训练效率低，容易过拟合，但如今算力提升，大数据时代数据增多，训练的过拟合风险降低，因此深度学习开始受到关注

一文看懂深度学习（白话解释+8个优缺点+4个典型算法）_weixin_43612023的博客-CSDN博客_深度学习的优势

问题和总结

​​

6 支持向量机SVM

SVM基本原理

基本思想：SVM的目标在数据特征空间寻找一个最优超平面将数据分成两类，这个最优化超平面使得离其最近的点到其的距离最大化，这些点被称为支持向量。SVM可以用于解决二分类或者多分类问题。​​

​​​​

 ​​

 SMO算法的基本思路：

1. 选取一对需要更新的变量ai和aj
2. 固定ai和aj以外的参数，求解6.11式

 核函数：升维，使得样本在高纬度线性可分(可以被超平面隔开)

​​

​​

软间隔和正则化

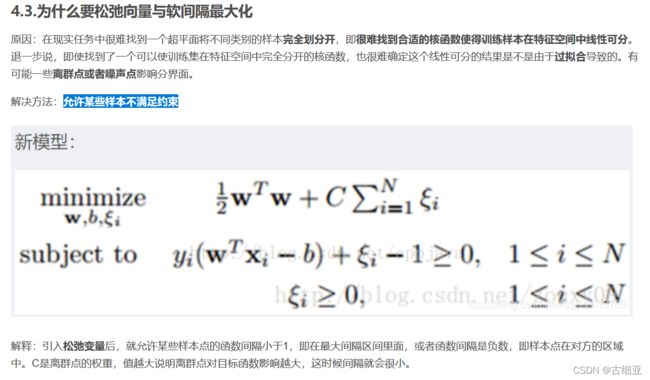
为什么引入“软间隔”概念？：

1. 现实中很难确定合适的核函数使样本在特征空间中线性可分
2. 即便是找到了这个核函数，也不能确定这个线性可分的结果是不是过拟合造成的
3. 缓解这个问题需要允许一部分样本在支持向量机SVM上出错，因此引入“软间隔”

    引入“松弛变量”，以表征该样本不满足约束的程度。

区别于SVM：

    SVM是要求所有样本均满足约束，所有样本都划分正确，也称“硬间隔”

支持向量回归SVR

支持向量回归(Support Vector Regression)_u014611178的博客-CSDN博客_支持向量回归

支持向量机不仅可以用于分类(SVM划分超平面)，还可以用于回归

支持向量机的精髓在于“间隔最大化”

1. 在分类SVM中，需要找到一个w和b使得靠近超平面的样本点间隔最大
2. 在回归SVR中，使靠超平面最远的样本点之间的间隔最大

带松弛变量的SVR

​

 问题和总结

​​

​​

 ​​

​​

​

7 贝叶斯分类器

贝叶斯思想：

​

先验概率：是指根据以往经验和分析得到的概率,如全概率公式

后验概率：可理解为条件概率

     先验概率的决策有很大的局限，但也有使用价值，例如：整合在朴素贝叶斯算法中，但先验概率需要样本量很大时才很准确

    引入“分类错误率”，后验概率越大，错误率越小，因此在贝叶斯分类器中，整合先验概率，后验概率来计算结果

但是最基础的贝叶斯分类器考虑了属性间的相关性，计算很麻烦，故引出朴素贝叶斯分类器

 朴素贝叶斯分类器(NB算法)

​

1，假设前提：属性相互独立

2，过程原理：基于训练集D，采用极大似然估计的方法，来估计先验概率P(Yk)和每个属性的条件概率P(Xi | Yk),训练完成后，根据朴素贝叶斯公式，计算出不同的分类值，取最大值作为结果

​

3，实践中常对“朴素贝叶斯分类器”的运算取对数，使连乘变为连加，避免了数值下溢

拉普拉斯平滑(拉普拉斯修正)：

如果在使用朴素贝叶斯分类器的过程中，样本集D没有出现对属性ａ＝ｘｘ的判断，那么在计算先验概率时，该ｐ就＝０，整个朴素贝叶斯算出来也是０，为了避免这种情况发生，在先验概率和条件概率的每个式子的分子分母都+1，这个+1操作对估计概率的变化可忽略不计，但可以有效避免０概率问题

​

 朴素贝叶斯优缺点

​

半朴素贝叶斯分类器

•  为了降低贝叶斯分类器中估计后验概率P(c | X)的难度，引入了朴素贝叶斯分类器——采用属性条件独立性假设
• 由于朴素贝叶斯分类器的“属性条件独立性假设”现实中很难成立，引入半朴素贝叶斯分类器 

基本思想：

        考虑部分属性间依赖关系，即不需要完全计算依赖，也不会忽略强依赖关系

常用策略：

        “独依赖估计ODE”：每个属性最多仅依赖一个其他属性(其后验概率能由其他属性的后验概率加权表示)        

贝叶斯网络

贝叶斯网络，又称信念网络，或有向无环图模型，是一种概率图模型。

简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。

​

8 集成学习

个体与集成

  集成学习：多分类器系统——通过构建并结合多个学习器来完成学习任务

  同质：“神经网络集成”中全都是神经网络，这样的同质集成中，个体学习器也称“基学习器”

  异质：一个集成中包含不同类型的个体学习器(如：同时包含决策树and神经网络)，这样的异质集成中，个体学习器也称“组件学习器”

  弱学习器：泛化性能略优于随即猜测的学习器(如：在二分类问题上精度略高于50%的分类器)；集成学习的很多研究都是针对弱学习器的。

集成学习的效果

​

个体分类器的数目 和 准确率 都影响着集成学习的最终效果！

集成学习的原则：

好而不同：个体学习器效果都不错，并且模型不同

少数服从多数：广义的少数服从多数

Boosting：个体学习器之间有强依赖关系

    何为强依赖关系？：下一个学习器的权重由上一轮的错误率e决定，而样本权重由分类器权重决定

    Boosting是集成学习中的一种方法，意为“提升”。提升是一个逐步优化集成学习器的过程，即每个个体学习器都在弥补集成学习器的欠缺，从而达到整体的优化。

    为什么权重的变化能达到整体的优化？：因为前面的判断正确，后面权重低，但学习器个数多，最终的判断正确概率>判断错误概率（少数服从多数）；而前面的判断错误，后面权重高，最终的判断正确概率>判断错误概率（权重增加的很多）

原理，思想：

• 集成学习含有多个个体学习器，对于某一个输入值，集成的判断结果由所有个体学习器加权决定。
• 每个个体学习器因为模型不同，各自的阈值，算法都不同，这可能导致同一个输入在不同的个体学习器中判断结果不同。
• 这就需要在不断的整合个体学习器时，每次都增加“之前被误判的样本数据”的权重，弥补集成学习器的欠缺，从而达到整体优化

（详见下方AdaBoost算法）

AdaBoost算法

Boosting族算法中最著名的是AdaBoost

https://zhuanlan.zhihu.com/p/27126737

​

 样本权重≠分类器权重

对于AdaBoost算法来说，样本权重由上一轮的错误率决定，作用域集成学习的过程中，可影响下一轮的学习器错误率；而分类器权重是判断预测时对各个分类器重要程度的评估，它由个体分类器的错误率决定。

 

Bagging：个体学习器之间相互独立

    何为相互独立？：采样的时候使用“自助法”，进行k轮抽取，得到k个训练集；但这种独立不是完全的独立，只是样本集之间差异较大，近似认为“独立”

Boosting和Bagging的区别

1. 训练集抽样：  Boosting全采用，Bagging自助法抽取
2. 串行、并行：  Boosting的算法中，Boosting会减小在上一轮训练正确的样本的权重，增大错误样本的权重，后一个模型参数需要前一轮模型的结果，因此为串行式集成学习；     Bagging的算法中，所有学习器之间没有关系，可以同时训练，因此为并行式集成学习；
3. 样例权重：    Boosting对正确的减小，对错误的增大；  Bagging则全部相同权重
4. 判断依据：    Boosting对不同学习器预测结果加权后判断 ；  Bagging简单的投票，少数服从多数。
5. 分类功能：    Boosting加权判断；Bagging投票判断
6. 回归功能：    Boosting加权求值；Bagging取各模型平均值

AdaBoost只适用于二分类问题(因为这个方法是判断yes或者no)，而Bagging能不经修改的用于多分类、回归等任务

随机森林RF：Bagging的一个扩展变体（随机属性选择）

RF在以决策树为基学习器，构建Bagging集成的基础上：引入了随机属性选择

为什么引入“随机属性选择”？：

在样本选取上RF和Bagging都是用自助法，但在决策树生成过程中，RF会从属性列表中随机选取部分属性用于分类，保证基分类器的多样性，因此个体学习器的性能会有所降低，但由于随机森林的“平均”特性，总体方差会更小

 RF虽然是决策树生成的，但RF是“随机属性型”决策树

 结合策略：平均法、投票法、学习法

​

      

问题和总结

加权平均不一定优于简单平均：某些权重过高会导致过拟合 

“绝对多”表示>50%  “相对多”表示>其他

硬投票：少数服从多数

软投票：要求每个模型都能估计概率，预测结果需要乘上各自的概率

 8.6 试析 Bagging 通常为何难以提升朴素贝叶斯分类器的性能.

​

8.7 试析随机森林为何比决策树 Bagging 集成的训练速度更快. 

​