算法:FloodFill算法
文章目录
- 算法原理
-
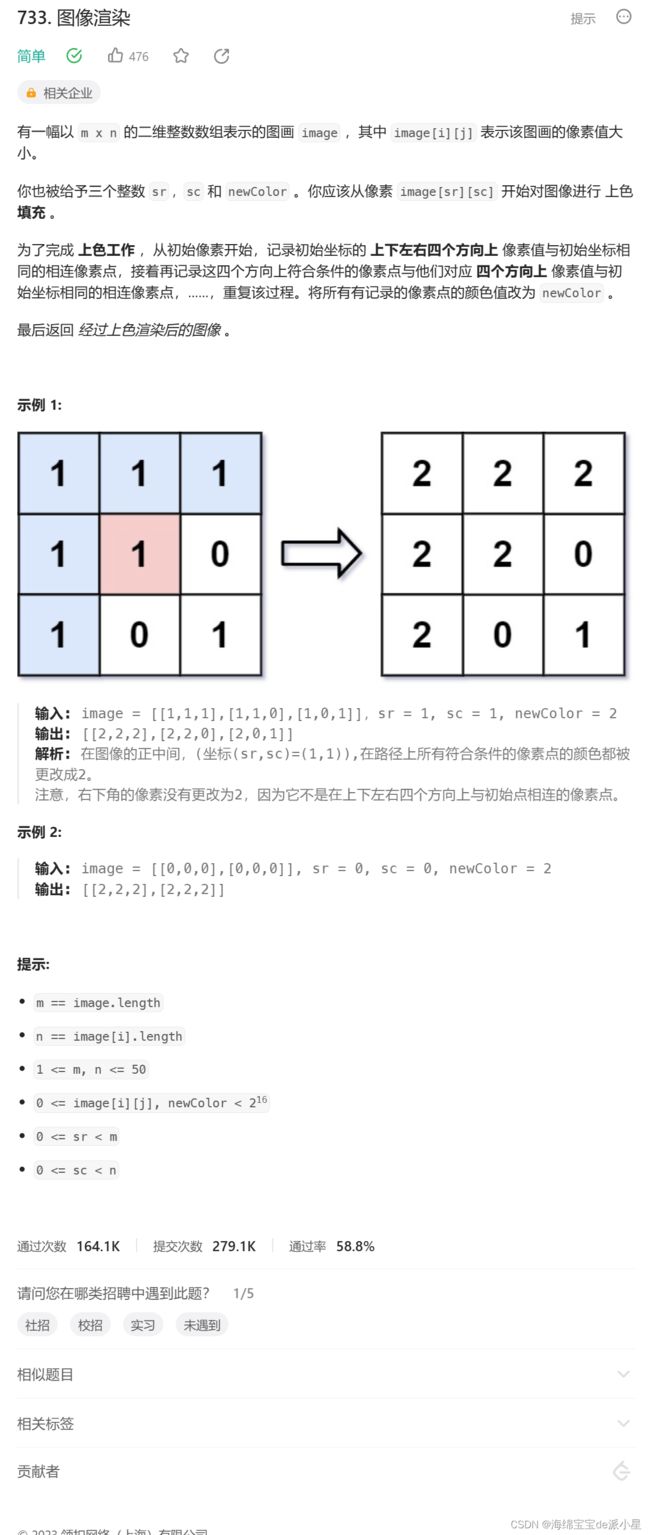
- 图像渲染
- 岛屿数量
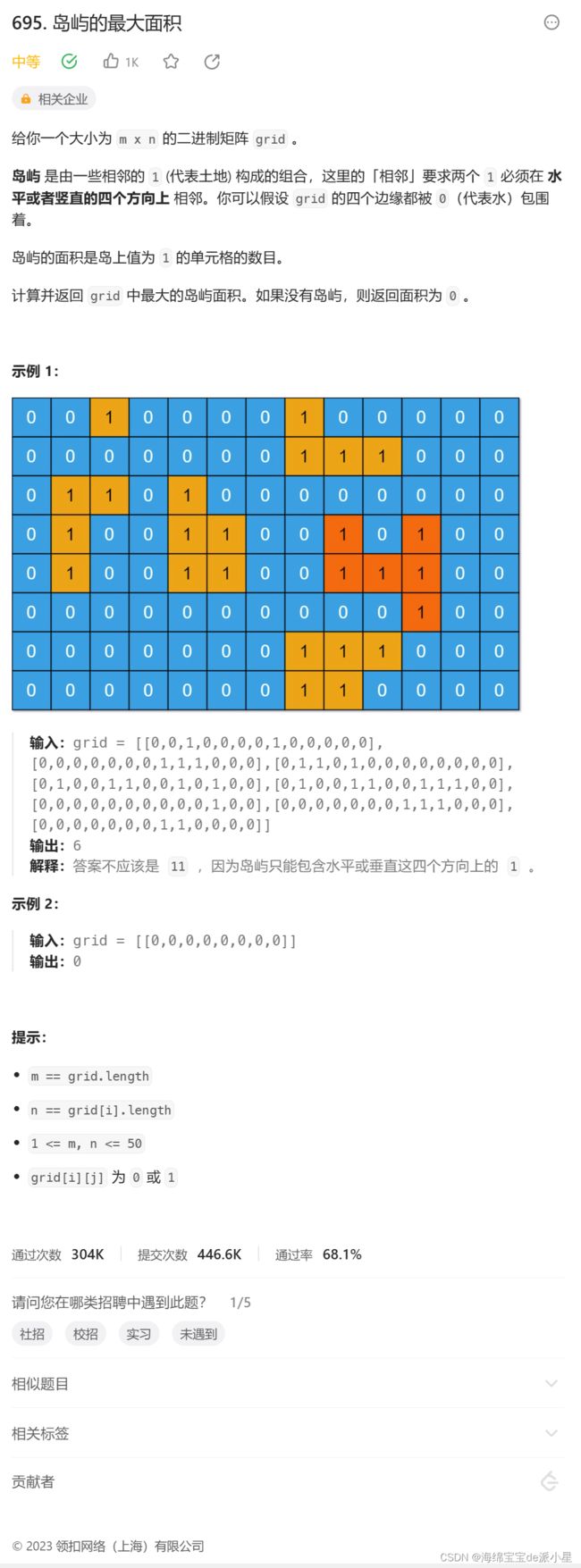
- 岛屿的最大面积
- 被围绕的区域
- 太平洋大西洋水流问题
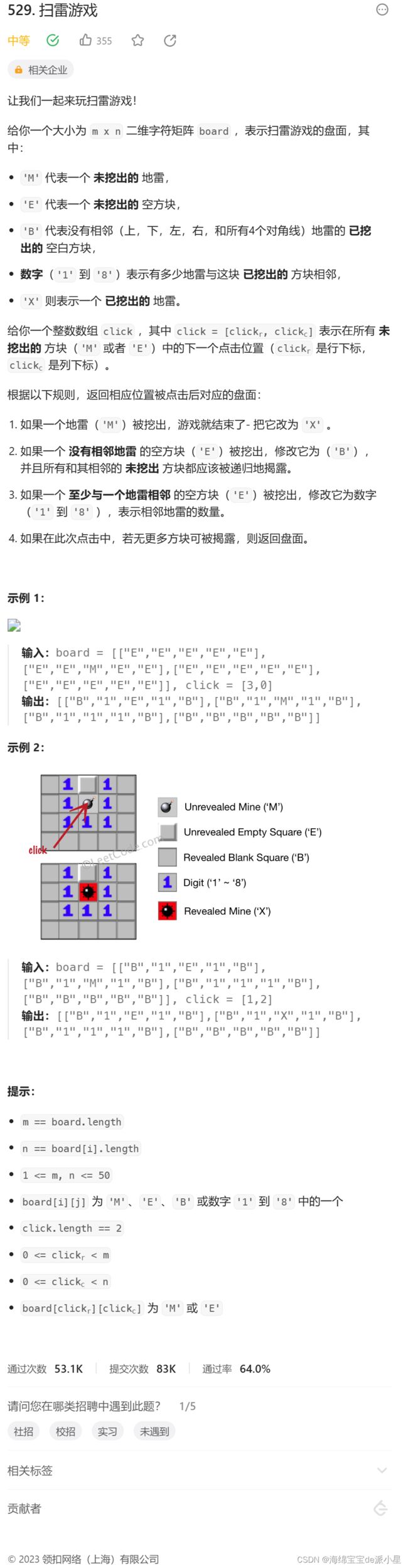
- 扫雷游戏
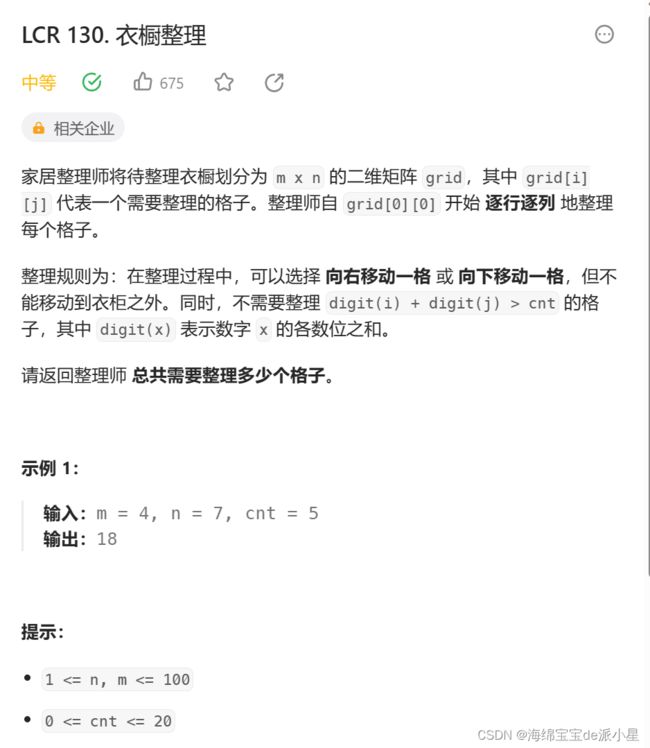
- 衣橱整理
算法原理
FLoodFill算法通俗来讲,就是洪水给地势带来的变化,而实际上题目要求的就是一个连通块问题,那本质还是暴搜和DFS/BFS相结合,下面用例题来解释
图像渲染
class Solution
{
public:
int newcolor;
int oldcolor;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<int>>& image, int i, int j)
{
if(image[i][j] != oldcolor)
{
return;
}
image[i][j] = newcolor;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < image.size() && y >= 0 && y < image[0].size() && image[x][y] == oldcolor)
{
dfs(image, x, y);
}
}
}
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
oldcolor = image[sr][sc];
newcolor = color;
if(newcolor == oldcolor)
return image;
dfs(image, sr, sc);
return image;
}
};
岛屿数量
class Solution
{
public:
// 全局变量
bool check[301][301];
int ret;
int m,n;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int numIslands(vector<vector<char>>& grid)
{
m = grid.size();
n = grid[0].size();
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == '1' && check[i][j] == false)
{
ret++;
dfs(grid, i, j);
}
}
}
return ret;
}
void dfs(vector<vector<char>>& grid, int i, int j)
{
check[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && check[x][y] == false)
{
dfs(grid, x, y);
}
}
}
};
岛屿的最大面积
一开始把path放到了函数中,每次path+1,但测试用例过不了,经过很长时间的调试后发现了问题的所在,问题在于是在搜索后如果回溯了,以前加过的path就会减掉,所以测试用例过不了,把path放到全局变量,每次统计完后统一进行恢复就不会出现这样的情况了
class Solution
{
public:
bool check[51][51];
int ret;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int m, n;
int path;
int maxAreaOfIsland(vector<vector<int>>& grid)
{
m = grid.size();
n = grid[0].size();
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == 1 && check[i][j] == false)
{
path++;
dfs(grid, i, j);
path = 0;
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid, int i, int j)
{
ret = max(ret, path);
check[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && check[x][y] == false && grid[x][y] == 1)
{
path++;
dfs(grid, x, y);
}
}
}
};
被围绕的区域
本题采用的是正难则反的思想
class Solution
{
public:
// 全局变量
int m, n;
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
void solve(vector<vector<char>>& board)
{
m = board.size();
n = board[0].size();
// 处理边界
for(int i = 0; i < m; i++)
{
if(board[i][0] == 'O')
dfs(board, i, 0);
if(board[i][n - 1] == 'O')
dfs(board, i, n - 1);
}
for(int i = 0; i < n; i++)
{
if(board[0][i] == 'O')
dfs(board, 0, i);
if(board[m - 1][i] == 'O')
dfs(board, m - 1, i);
}
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(board[i][j] == 'O')
board[i][j] = 'X';
if(board[i][j] == '.')
board[i][j] = 'O';
}
}
}
void dfs(vector<vector<char>>& board, int i, int j)
{
board[i][j] = '.';
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O')
{
dfs(board, x, y);
}
}
}
};
太平洋大西洋水流问题
class Solution
{
public:
int m, n;
bool check1[201][201];
bool check2[201][201];
int dx[4] = { 1, -1, 0, 0 };
int dy[4] = { 0, 0, 1, -1 };
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
vector<vector<int>> ret;
m = heights.size();
n = heights[0].size();
for (int i = 0; i < n; i++)
{
dfs1(heights, 0, i);
dfs2(heights, m - 1, i);
}
for (int i = 0; i < m; i++)
{
dfs1(heights, i, 0);
dfs2(heights, i, n - 1);
}
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (check1[i][j] ==true && check2[i][j] == true)
{
ret.push_back({ i, j });
}
}
}
return ret;
}
void dfs1(vector<vector<int>>& board, int i, int j)
{
check1[i][j] = true;
for (int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] >= board[i][j] && check1[x][y] == false)
{
dfs1(board, x, y);
}
}
}
void dfs2(vector<vector<int>>& board, int i, int j)
{
check2[i][j] = true;
for (int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] >= board[i][j] && check2[x][y] == false)
{
dfs2(board, x, y);
}
}
}
};
扫雷游戏
class Solution
{
public:
int dx[8] = { 0, 0, 1, -1, 1, 1, -1, -1 };
int dy[8] = { 1, -1, 0, 0, 1, -1, 1, -1 };
int m, n;
bool check[51][51];
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
{
int i = click[0], j = click[1];
m = board.size(), n = board[0].size();
// 挖到地雷
if (board[i][j] == 'M')
{
board[i][j] = 'X';
return board;
}
// 挖到空方块,开始递归
dfs(board, i, j);
return board;
}
void dfs(vector<vector<char>>& board, int i, int j)
{
int count = 0;
for (int k = 0; k < 8; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M' && check[x][y] == false)
{
// 统计一下四周雷的个数
count++;
}
}
if (count)
{
board[i][j] = count + '0';
return;
}
else
{
board[i][j] = 'B';
for (int k = 0; k < 8; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E')
{
// 如果周围的格子不是雷,就递归
dfs(board, x, y);
}
}
}
}
};
衣橱整理
class Solution
{
public:
int dx[2] = {0, 1};
int dy[2] = {1, 0};
int ret;
int m, n, cnt;
bool check[101][101];
int func(int m)
{
int count = 0;
while(m)
{
count += m % 10;
m = m / 10;
}
return count;
}
int wardrobeFinishing(int _m, int _n, int _cnt)
{
m = _m;
n = _n;
cnt = _cnt;
dfs(0, 0);
return ret;
}
void dfs(int i, int j)
{
check[i][j] = true;
ret++;
for(int k = 0; k < 2; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x < m && y < n && check[x][y] == false && func(x) + func(y) <= cnt)
{
dfs(x, y);
}
}
}
};