力扣第42题 接雨水 C++ 动态规划 + 单调栈 + 双指针 Java总代码 都有
题目
42. 接雨水
困难
相关标签
栈 数组 双指针 动态规划 单调栈
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
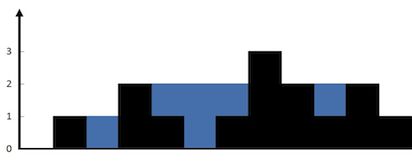
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
思路和解题方法 一 动态规划
- 首先,它创建了两个数组 leftMax 和 rightMax 分别用来存储每个位置左边和右边的最大高度。这一步是为了在计算每个位置能接到的雨水量时,可以方便地找到左右两边的最大高度。
- 接着,通过两个 for 循环分别计算出每个位置左边和右边的最大高度。这样就将原本需要每次遍历数组来找到左右最大高度的操作,通过动态规划的方法,只需要遍历数组两次就得到了左右两边的最大高度数组。
- 最后,再通过一个 for 循环,计算每个位置能接到的雨水量并累加起来,最终得到总的接雨水量。
复杂度
时间复杂度:
O(n)
时间复杂度为 O(n),其中 n 为输入数组的长度。这是因为在两次遍历数组的过程中,分别计算了左边和右边的最大高度,以及通过一次遍历计算每个位置能接到的雨水量,所以总体时间复杂度为 O(n)。
空间复杂度
O(n)
空间复杂度也是 O(n),因为使用了两个大小为 n 的辅助数组 leftMax 和 rightMax 来存储每个位置左右两边的最大高度,这些额外的空间占用是与输入规模 n 成正比的。
c++ 代码 1
class Solution {
public:
int trap(vector& height) {
int n = height.size();
if (n == 0) {
return 0; // 如果输入数组为空,则无法接到雨水,直接返回 0
}
vector leftMax(n); // 用于存储每个位置左边的最大高度
leftMax[0] = height[0]; // 第一个位置的最大高度即为本身的高度
for (int i = 1; i < n; ++i) {
leftMax[i] = max(leftMax[i - 1], height[i]); // 计算每个位置左边的最大高度
}
vector rightMax(n); // 用于存储每个位置右边的最大高度
rightMax[n - 1] = height[n - 1]; // 最后一个位置的最大高度即为本身的高度
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = max(rightMax[i + 1], height[i]); // 计算每个位置右边的最大高度
}
int ans = 0; // 用于累加接到的雨水总量
for (int i = 0; i < n; ++i) {
ans += min(leftMax[i], rightMax[i]) - height[i]; // 计算每个位置能接到的雨水量并累加
}
return ans; // 返回接到的雨水总量
}
};
思路和解题方法 二 单调栈
在这个问题中,我们需要找到每个位置上方能存储的雨水量。对于任意位置 i,其上方能存储的雨水量取决于左边最高柱子的高度 lHeight 和右边最高柱子的高度 rHeight。
为了找到左右两边的最高柱子高度,代码中使用了两个循环来遍历数组。对于每个位置 i,分别向左和向右找到比当前位置高度还高的柱子,记录其高度。
这种遍历方式会导致时间复杂度为 O(n^2),因为对于每个位置,都需要线性时间来寻找左右两边的最高柱子高度。
如果使用单调栈的思想来解决这个问题,可以将时间复杂度降低到 O(n)。具体思路如下:
创建一个单调递减栈,用来存储柱子的下标,而不是直接存储高度。
从左到右遍历柱子,如果当前柱子的高度小于栈顶柱子的高度,则将当前柱子的下标入栈;否则,说明当前柱子可能能形成一个凹槽,可以接到雨水。
当遇到比栈顶高度大的柱子时,说明当前柱子可能会结束之前形成的凹槽。此时可以弹出栈顶元素,计算当前柱子与栈顶柱子之间的距离,并根据高度差计算接到的雨水量。
遍历完成后,所有能接到雨水的凹槽都处理完了,累加得到的雨水总量即为最终答案。
复杂度
时间复杂度:
O(n)
时间复杂度: O(n),其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。
空间复杂度
O(1)
空间复杂度: 0(1)。只需要使用常数的额外空间。
c++ 代码 2
class Solution {
public:
int trap(vector& height) {
int sum = 0; // 用于记录接到的雨水总量
for (int i = 0; i < height.size(); i++) { // 遍历每根柱子
// 第一个柱子和最后一个柱子不接雨水,直接跳过
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度,初始化为当前柱子的高度
int lHeight = height[i]; // 记录左边柱子的最高高度,初始化为当前柱子的高度
// 寻找右边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
// 寻找左边柱子的最高高度
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i]; // 计算当前柱子能接到的雨水高度
if (h > 0) sum += h; // 如果能接到雨水,则累加到总量上
}
return sum; // 返回接到的雨水总量
}
};
思路和解题方法 三 双指针优化
- 使用了两个指针 left 和 right 分别指向数组的左右两端,同时使用两个变量 leftMax 和 rightMax 来表示左指针和右指针所遍历过的位置的最大高度。然后通过一个 while 循环来不断移动左右指针,并更新 leftMax 和 rightMax 来计算能接到的雨水量。
- 在循环中,每次比较当前左右指针所指向位置的高度,选择较小高度的一侧进行处理。如果左指针所指的高度小于右指针所指的高度,则计算左侧能接到的雨水量,并将左指针向右移动;反之,计算右侧能接到的雨水量,并将右指针向左移动。直至左右指针相遇,表示整个数组遍历完成,计算接雨水的总量并返回。
- 这种方法省去了使用额外空间存储左右两边最大高度的数组,而是通过双指针实时更新最大高度,从而降低了空间复杂度。
复杂度
时间复杂度:
O(n)
时间复杂度是 O(n),其中 n 是输入数组的长度,因为算法需要遍历一次输入数组来计算接雨水的总量。
空间复杂度
O(1)
空间复杂度是 O(1),因为算法只使用了有限数量的额外变量来存储左右指针、左右两侧的最大高度和接雨水的总量
c++ 代码 3
class Solution {
public:
int trap(vector& height) {
int ans = 0; // 初始化接水量为0
int left = 0, right = height.size() - 1; // 初始化左右指针分别指向数组的两端
int leftMax = 0, rightMax = 0; // 初始化左右两侧的最大高度
while (left < right) { // 当左右指针没有相遇时进行循环
leftMax = max(leftMax, height[left]); // 更新左侧的最大高度
rightMax = max(rightMax, height[right]); // 更新右侧的最大高度
if (height[left] < height[right]) { // 如果左侧的高度小于右侧
ans += leftMax - height[left]; // 计算左侧能接到的雨水量,并累加到结果中
++left; // 左指针向右移动
} else { // 如果右侧的高度小于等于左侧
ans += rightMax - height[right]; // 计算右侧能接到的雨水量,并累加到结果中
--right; // 右指针向左移动
}
}
return ans; // 返回总的接水量
}
};
Java代码 总
一 动态规划
class Solution {
public int trap(int[] height) {
int n = height.length; // 获取数组的长度
if (n == 0) { // 如果数组长度为0,直接返回0
return 0;
}
int[] leftMax = new int[n]; // 创建一个数组用于存储每个位置左侧的最大高度
leftMax[0] = height[0]; // 初始化第一个位置的左侧最大高度为数组第一个元素的高度
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]); // 计算每个位置左侧的最大高度
}
int[] rightMax = new int[n]; // 创建一个数组用于存储每个位置右侧的最大高度
rightMax[n - 1] = height[n - 1]; // 初始化最后一个位置的右侧最大高度为数组最后一个元素的高度
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]); // 计算每个位置右侧的最大高度
}
int ans = 0; // 初始化接水量为0
for (int i = 0; i < n; ++i) { // 遍历每个位置
ans += Math.min(leftMax[i], rightMax[i]) - height[i]; // 计算每个位置能接到的雨水量,并累加到结果中
}
return ans; // 返回总的接水量
}
}
二 单调栈
class Solution {
public int trap(int[] height) {
int ans = 0; // 初始化接水量为0
Deque stack = new LinkedList(); // 使用栈来记录数组下标
int n = height.length; // 获取数组的长度
for (int i = 0; i < n; ++i) { // 遍历数组
while (!stack.isEmpty() && height[i] > height[stack.peek()]) { // 当当前高度大于栈顶高度时,意味着可以计算当前位置能接到的雨水量
int top = stack.pop(); // 弹出栈顶元素作为当前位置的最低点
if (stack.isEmpty()) { // 如果栈为空,意味着无法形成凹槽,结束当前计算
break;
}
int left = stack.peek(); // 获取栈顶元素作为左边界
int currWidth = i - left - 1; // 计算当前宽度
int currHeight = Math.min(height[left], height[i]) - height[top]; // 计算当前高度
ans += currWidth * currHeight; // 累加到结果中
}
stack.push(i); // 将当前位置下标入栈
}
return ans; // 返回总的接水量
}
}
三 双指针
class Solution {
public int trap(int[] height) {
int ans = 0; // 初始化接水量为0
int left = 0, right = height.length - 1; // 定义左右指针分别指向数组的首尾
int leftMax = 0, rightMax = 0; // 初始化左侧最大高度和右侧最大高度为0
while (left < right) { // 当左指针小于右指针时进行循环
leftMax = Math.max(leftMax, height[left]); // 更新左侧最大高度
rightMax = Math.max(rightMax, height[right]); // 更新右侧最大高度
if (height[left] < height[right]) { // 如果左侧高度小于右侧高度
ans += leftMax - height[left]; // 计算并累加左侧能接到的雨水量
++left; // 左指针右移
} else { // 如果左侧高度大于等于右侧高度
ans += rightMax - height[right]; // 计算并累加右侧能接到的雨水量
--right; // 右指针左移
}
}
return ans; // 返回总的接水量
}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。