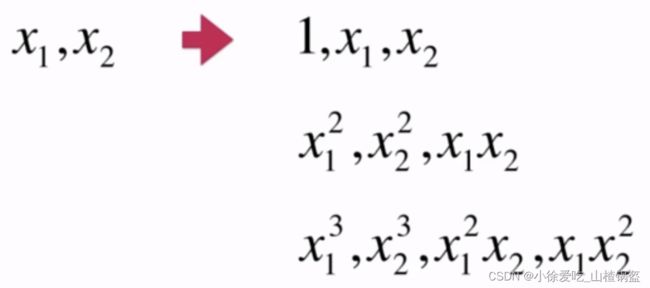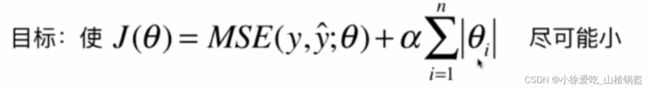05机器学习--多项式回归与模型泛化及python实现
目录
①什么是多项式回归
②scikit-learn中的多项式回归和Pipelin
③过拟合与欠拟合
④验证数据集与交叉验证
⑤回顾网格搜索
⑥偏差方差权衡
⑦解决过拟合问题--模型正则化1--岭回归
⑧解决过拟合问题--模型正则化2--LASSO回归
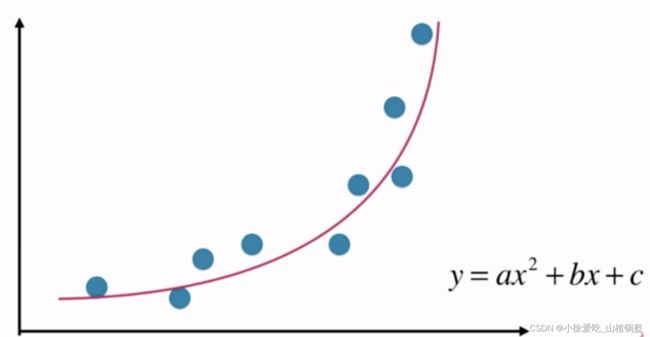
①什么是多项式回归
我们把![]() 看做是这个式子的一个特征,x为另外一个特征,从这个角度来看,这个式子其实还是一个线性回归;但是单从x的角度来说,这是一个非线性方程,这就是多项式回归;相当于我们为我们的样本多增加了特征,但是这个特征就是我们样本原来样本的多项式项 ,用线性回归的思路更好的拟合原来的数据,但是本质上求出来的是非线性曲线,对数据集升维
看做是这个式子的一个特征,x为另外一个特征,从这个角度来看,这个式子其实还是一个线性回归;但是单从x的角度来说,这是一个非线性方程,这就是多项式回归;相当于我们为我们的样本多增加了特征,但是这个特征就是我们样本原来样本的多项式项 ,用线性回归的思路更好的拟合原来的数据,但是本质上求出来的是非线性曲线,对数据集升维
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
plt.scatter(x, y)
plt.show()结果输出:
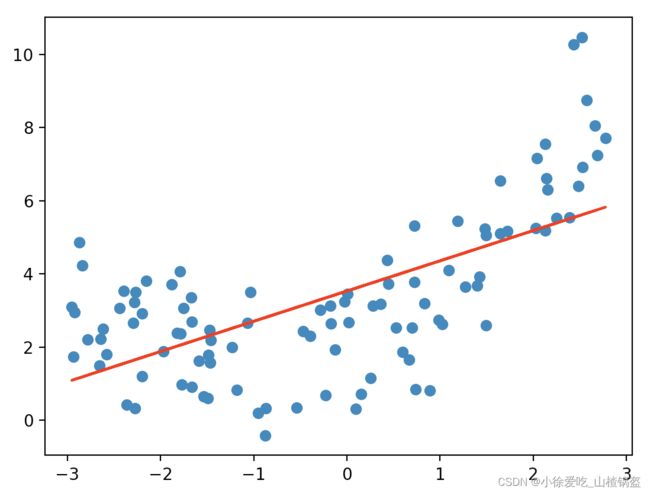
首先用线性回归拟合一下
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
# plt.scatter(x, y)
# plt.show()
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()结果输出:
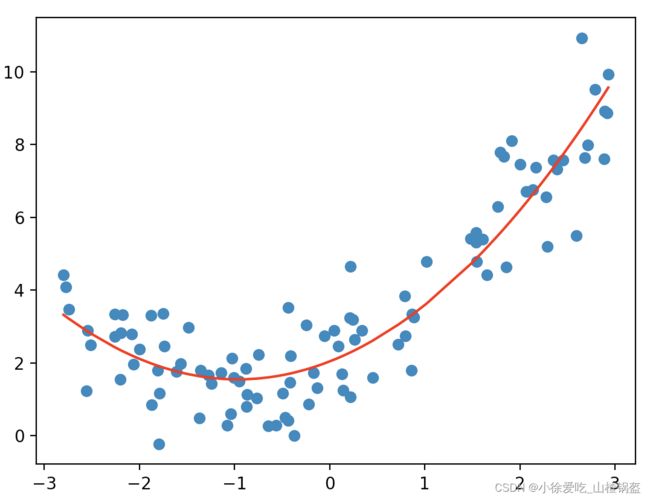
改进一下,多项式回归(添加一个特征)
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
# plt.scatter(x, y)
# plt.show()
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
# plt.scatter(x, y)
# plt.plot(x, y_predict, color='r')
# plt.show()
X2 = np.hstack([X, X**2])
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()结果输出:
②scikit-learn中的多项式回归和Pipelin
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2) # 为原本的数据集添加最多几次幂的特征
poly.fit(X)
X2 = poly.transform(X) # 转换为多项式特征,有三列,从0次幂一直到2次幂
from sklearn.linear_model import LinearRegression
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()结果输出:
关于PolynomialFeatures
本身有两个特征,升维到3个特征时
PolynomialFeatures(degree=3)时,最终会生成十列(0次幂、1次幂、2次幂、3次幂)
Pipeline方法:(没有专门的多项式回归类,用这个方法可以简单的创建自己的多项式回归类)
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
poly_reg = Pipeline([ # 按着每一个步骤依次进行
("poly", PolynomialFeatures(degree=2)), # 多项式特征
("std_scaler", StandardScaler()), # 数据归一化
("lin_reg", LinearRegression()) # 回归
])
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()结果输出:
③过拟合与欠拟合
看一个夸张的例子,给上面的数据增加特征到100个
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
# 使用多项式回归
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)
y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()结果输出:(过拟合,个人理解:他在你给定的数据集上拟合很完美,但是预测的效果会差很多)
欠拟合:算法所训练的模型不能完整的表述数据关系
过拟合:算法所训练的模型过多的表达了数据间的噪音关系
泛化能力:根据训练数据得到上面的曲线,但是他在预测新的数据的时候,其实准确率很差,也说他泛化能力很差。
我们真正需要的是模型的泛化能力很好。
训练数据集与测试数据集的目的就是为了解决泛化能力不强的问题
④验证数据集与交叉验证
问题:对测试数据集过拟合了怎么办?我们一直都在针对测试集进行调参
解决方法:
数据集分为训练集、验证集(测试模型效果)、测试集(不参与模型的创建过程、模拟未知数据)
测试数据集衡量模型最终效能,验证集用来调参
问题:过拟合验证集怎么办?
解决方法:
交叉验证,把训练集分成k份,让k份数据分别去做验证集,剩下的就当做训练集,每一种组合都可以得到一个模型,把所有模型的性能平均值作为最终的新能结果,之后在判断是否调参
import numpy as np
from sklearn import datasets
# 手写识别数据集
digits = datasets.load_digits()
X = digits.data
y = digits.target
# 划分训练集测试集的方法
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
# 观察kNN的效果
from sklearn.neighbors import KNeighborsClassifier
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
knn_clf.fit(X_train, y_train)
score = knn_clf.score(X_test, y_test)
if score > best_score:
best_k, best_p, best_score = k, p, score
print("训练集与测试集的效果:")
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
# 交叉验证的方法
from sklearn.model_selection import cross_val_score # 默认分成五份交叉验证
# 手动限制的话可以添加参数cv比如cv=5分成五份
knn_clf = KNeighborsClassifier()
cross_val_score(knn_clf, X_train, y_train)
# 观察kNN的效果
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
scores = cross_val_score(knn_clf, X_train, y_train) # 每一次的分数
score = np.mean(scores) # 取均值
if score > best_score:
best_k, best_p, best_score = k, p, score
print("交叉验证的效果:")
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)结果输出:
两个方法的结果有区别,但是我们更相信交叉验证的结果,交叉验证通常不会过拟合某一组数据,所以平均来讲分数会低一些
⑤回顾网格搜索
网格搜索的本质就是交叉验证调参
import numpy as np
from sklearn import datasets
# 手写识别数据集
digits = datasets.load_digits()
X = digits.data
y = digits.target
# 划分训练集测试集的方法
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
from sklearn.neighbors import KNeighborsClassifier
# 交叉验证的方法
from sklearn.model_selection import cross_val_score
knn_clf = KNeighborsClassifier()
cross_val_score(knn_clf, X_train, y_train)
# 网格搜索
from sklearn.model_selection import GridSearchCV # CV就是交叉验证的意思
param_grid = [
{
'weights': ['distance'],
'n_neighbors': [i for i in range(2, 11)],
'p': [i for i in range(1, 6)] # 5 * 9 = 45组参数,每组分成5份
}
]
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)
print(grid_search.best_score_) # 最佳分数
print(grid_search.best_params_) # 最佳参数
best_knn_clf = grid_search.best_estimator_ # 最佳参数对应的最佳分类器
print(best_knn_clf.score(X_test, y_test))结果输出:
交叉验证的缺点是比较慢,但是最终找到的参数比较信赖,极端情况:留一法(LOO-CV),训练数据集有几个样本就分成几份,训练m-1份,留1份进行验证,缺点是计算量巨大(一般不使用)
⑥偏差方差权衡
左下角就是偏差,右上角就是方差,上面一组就是低偏差,下面一组就是高偏差,左边一组就是低方差,右边一组就是高方差
模型误差:偏差+方差+不可避免的误差(不可避免)
高偏差:比如欠拟合
高方差:比如模型太过复杂,kNN天生就是高方差(对数据特别敏感),参数学习一般都是高方差,一般可以减少数据维度,降噪,增加数据规模解决
两者一般是相互矛盾的,需要取一个权衡
⑦解决过拟合问题--模型正则化1--岭回归
思路:限制系数的大小(像上面过拟合的那个例子,会发现拟合的曲线非常弯曲,所以每一个特征的系数都会很大)
解决方法:改变损失函数
优化后,需要考虑让每theta尽可能小 ,阿尔法表示权重,不同的数据取值不同
岭回归实现
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.metrics import mean_squared_error
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
y_poly_predict = poly_reg.predict(X_test)
print('均方误差')
print(mean_squared_error(y_test, y_poly_predict)) # 均方误差,显然过拟合了
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)
# 封装绘制函数
def plot_model(model):
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:, 0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
plot_model(poly_reg)
# 岭回归
from sklearn.linear_model import Ridge
def RidgeRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("ridge_reg", Ridge(alpha=alpha)) # 比重
])
ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)
y1_predict = ridge1_reg.predict(X_test)
print('岭回归均方误差')
print(mean_squared_error(y_test, y1_predict))
plot_model(ridge1_reg)
# 调整alpha
ridge2_reg = RidgeRegression(20, 1)
ridge2_reg.fit(X_train, y_train)
y2_predict = ridge2_reg.predict(X_test)
print('岭回归均方误差')
print(mean_squared_error(y_test, y2_predict))
plot_model(ridge2_reg)
# 再调整alpha
ridge3_reg = RidgeRegression(20, 100)
ridge3_reg.fit(X_train, y_train)
y3_predict = ridge3_reg.predict(X_test)
print('岭回归均方误差')
print(mean_squared_error(y_test, y3_predict))
plot_model(ridge3_reg)结果输出:
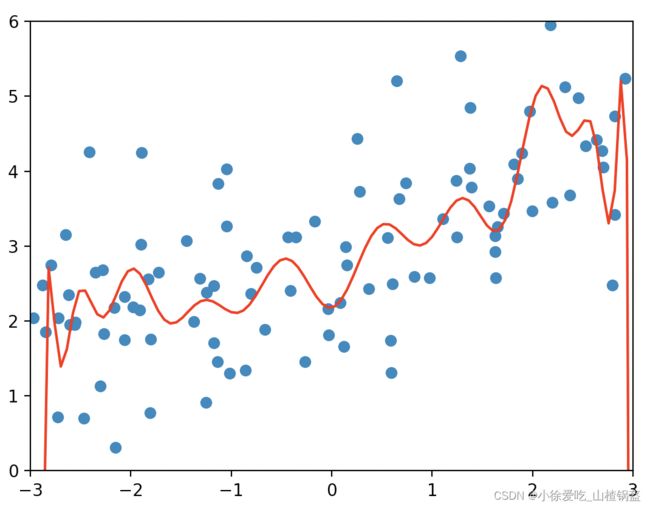
过拟合情况
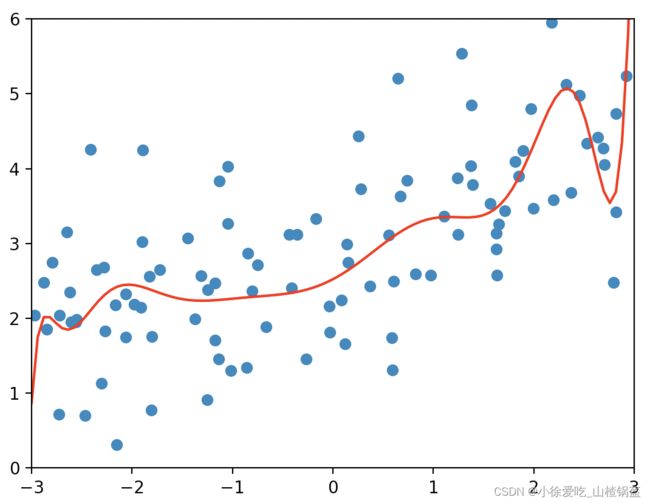
岭回归
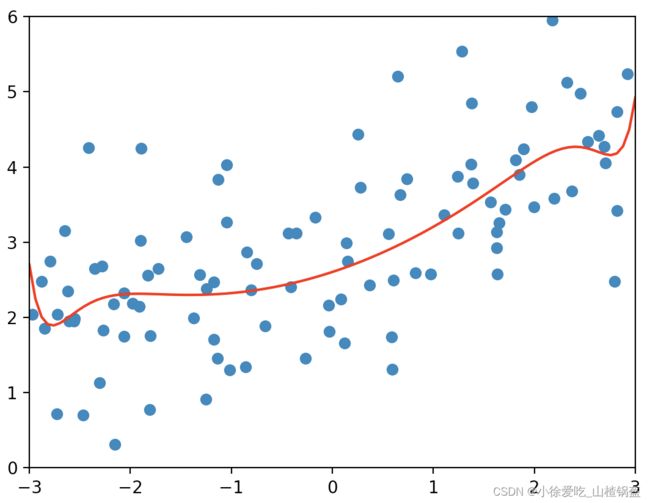
提高比重
在提高比重
⑧解决过拟合问题--模型正则化2--LASSO回归
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.metrics import mean_squared_error
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
y_poly_predict = poly_reg.predict(X_test)
print('均方误差')
print(mean_squared_error(y_test, y_poly_predict)) # 均方误差,显然过拟合了
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)
# 封装绘制函数
def plot_model(model):
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:, 0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
plot_model(poly_reg)
# LASSO回归
from sklearn.linear_model import Lasso
def LassoRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lasso_reg", Lasso(alpha=alpha))
])
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)
y1_predict = lasso1_reg.predict(X_test)
print('LASSO回归均方误差')
print(mean_squared_error(y_test, y1_predict))
plot_model(lasso1_reg)LASSO回归输出:
了解:LASSO回归趋向于使一部分theta为0(相当于选择了一些特征),可以当做特征选择用, 可能错误的忽略掉一些有用的特征,还是岭回归更可靠一些
扩展:
L0正则:希望theta的个数尽量小
弹性网: