蒙特卡洛方法、蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS) 学习

提出一个问题：
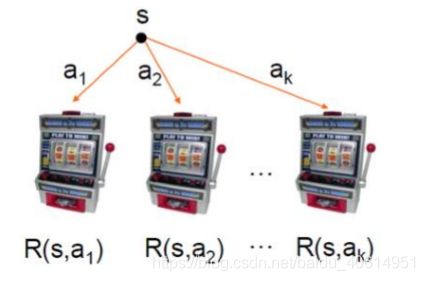
假设你当前有n个币，面前有k个赌博机。每个赌博机投一个币后摇动会产生随机的产出，你会怎么摇？

1. 从多臂赌博机说起

蒙特卡洛方法利用了一个基本的思想：随机模拟。根据大数定理、多次采样最终得到的样本均值可以估计变量的期望。
现代的(随机模拟)统计模拟方法由数学家乌拉姆提出、由Metropolis命名为蒙特卡洛方法、蒙特卡洛是一个著名的赌场、赌博总是和统计相关联的，于是我们也从赌博说起，谈谈多臂赌徒机。

你可能会选一个自己的幸运数字，然后只要那一个(通常这样你并不会幸运)。你也可能先每一个都摇一次、探索一遍、然后逮着产出最多的那个摇动，但是这样你可能会错过一个期望产出更高的机器，只是这个机器你第一次摇动正好产出较低。这就产生了一个问题：我该如何利用我现在有的信息、同时也不错失更好的机会？

有一种方法用来解决这一探索与利用问题：Upper Confidence Bound （UCB)

2. UCB

UCB用来解决探索与利用这一对矛盾。
他记录每个机器的以往的平均收获, 下一次选择UCB值最好的一个机器：
$$I_t=max\{X_{i,T_i(t-1)}+c_{t-1,Ti(t-1)}\}$$
其中：
$$T_i(t)=\sum _{s=1}^t\prod (I_s=i)$$
也就是到t次的时候、摇动过i这个机器的次数。
$$X_{i,T_i(t-1)}$$
是以往的i机器的平均收获，鼓励利用。

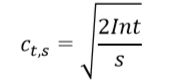
c是一个鼓励探索的项，如果一个机器要懂得越少，s越小、这项越大。

UCB算法的伪代码如下：

3. 蒙特卡洛树搜索

蒙特卡洛树搜说就是将蒙特卡洛方法这种随机模拟的方法应用到树搜索上。

传统的搜索算法例如MINMAX-SEARCH，在某个节点(状态)时、利用一个评估函数EVALUE(node)精确的评估该节点的价值，但是当搜索空间巨大的时候、这个方法就可能会超出算力(当然存在截断搜索的MINMAX)。

蒙特卡洛树搜索通过蒙特卡洛模拟来估计该节点的价值，而不是用一个评估函数。

蒙特卡洛树搜索可以分作选择(Selection)、拓展(Expansion)、模拟(simulation)、反向传播(backpropagation)四个阶段：

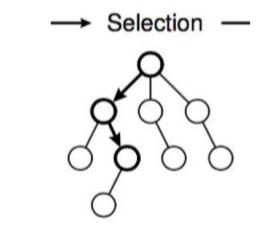
3.1选择阶段
从父节点(首次从根节点)开始、向下选择一个最急迫需要被拓展的节点：

• 该节点的所有动作都可能被拓展过：用UCB算法选择一个具有最大UCB值的子节点继续检查、向下迭代。
• 该节点还有一些没有被拓展：随机选取一个动作拓展
• 节点是一个终止节点(游戏结束)：反向传播
  
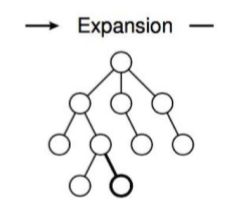
  3.2 拓展
  在选择的时候、我们找到了一个需要被拓展的节点N,以及一个动作A。在执行了A后状态变为N',将N'作为N的子节点
  
  3.3 模拟
  从新节点N'开始，让游戏随机的进行，得到一个游戏结局，该结局作为这一点的评分。
  
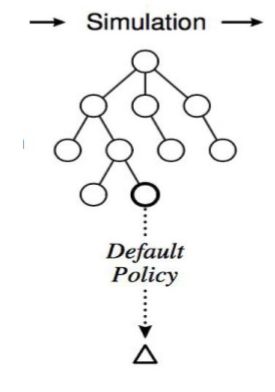
  3.4 反向传播
  在N‘的模拟结束后、从N'到根节点都会根据这次模拟的结果修改自己的估值。
  

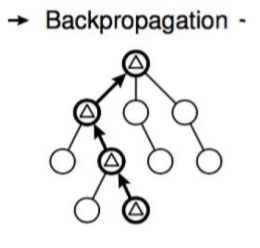
选择和拓展阶段被称作Tree Policy. 随机模拟阶段被称为Default Policy.
蒙特卡洛树搜索的大致伪代码如下：

一个简单的例子：

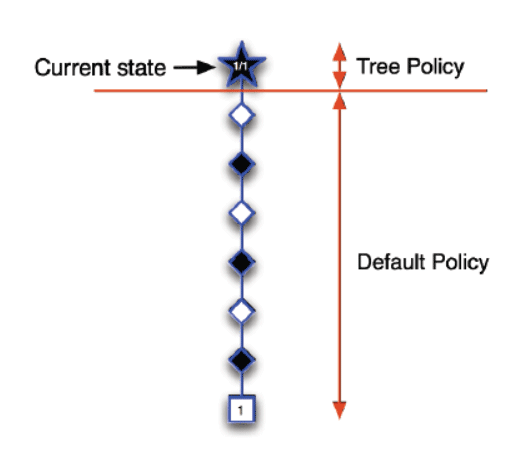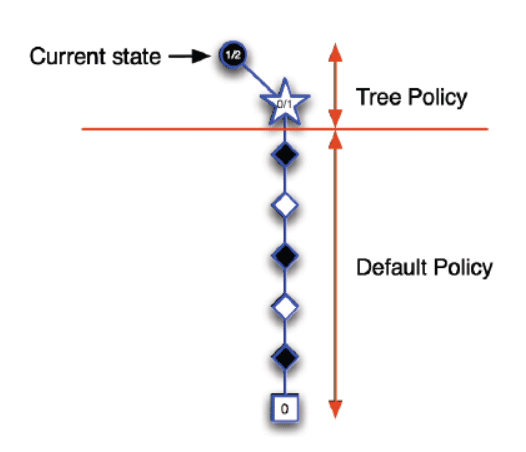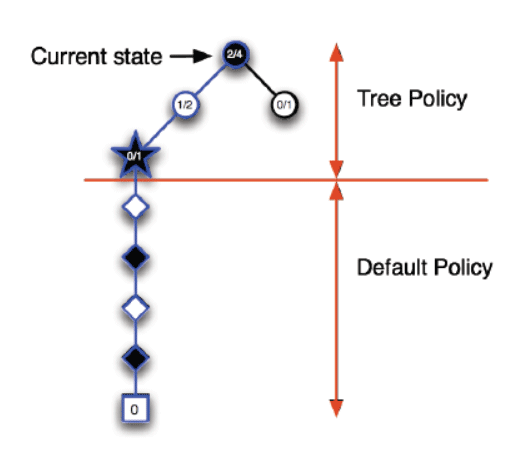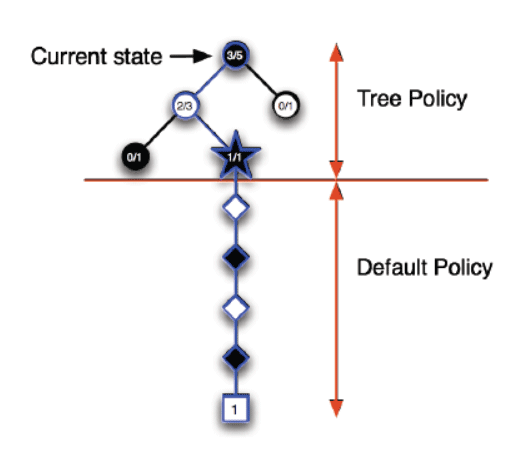
这只是蒙特卡洛方法的简述、具体的来看下UCB算法是如何应用在蒙特卡洛树搜索中的。

4. 伪代码

首先阐明一些符号的概念：

s(v): 与节点v相关的状态
a(v): 导致v状态的动作
N(v): 访问过v的次数
Q(v): 总共的对于v的仿真reword

总体的,对于当前的状态、应用蒙特卡洛树搜索、找到其子节点以及用模拟的方法确定该节点的值，返回一个具有最佳的reward的子节点。

function MCTS(s0)
	create root node v0 with state s0
	while within computational budget do
		vl <- TreePolicy(v0)
		delta <- DefaultPolicy(s(vl))
		BackUp(vl,delta)
	return a(BestChild(v0,0))

TreePolicy

对当前节点拓展或者选一个最佳子节点进行拓展。

function TreePolicy(v)
	while v is nonterinal do
		if v is not fully expanded then
			return Expand(v)
		else
			v < BestChild(v,Cp)
	return v

子节点选择
这里使用的UCB和之前介绍的有一些不一样，它在鼓励探索的一项前添加了一个系数：

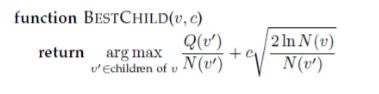
拓展

function Expand(v)
	choose a in untried acions from A(s(v))
	add a new child v' to v
		with s(v') = f(s(v),a) #f表示一个从（state,action)到state的映射
		and a(v') = a
	return v'

DefaultPolicy

function DefaultPolicy(s)
	while s is non-terminal do
		choose a in A(s) uniformly at random #随机选择一个动作
		s <- f(s,a)
	return reward for state s

BackUp

function BackUp(v,delta)
	while v is not null do
		N(v) <- N(v) + 1
		Q(v) <- Q(v) + delta
		v <- parent of v

写完这些感觉梳理了下思路，下一次开始写一个黑白棋的蒙特卡洛搜索程序。
感谢

1. 吴飞 - 《人工智能》mooc
2. https://www.cnblogs.com/LittleHann/p/11608182.html#_labelTop
3. https://mp.weixin.qq.com/s?__biz=MzA5MDE2MjQ0OQ==&mid=2652786766&idx=1&sn=bf6f3189e4a16b9f71f985392c9dc70b&chksm=8be52430bc92ad2644838a9728d808d000286fb9ca7ced056392f1210300286f63bd991bde84#rd