吴恩达《机器学习》课堂笔记与课后练习题的详细题解
Week 1
课程链接:https://www.bilibili.com/video/BV164411b7dx
这是本人的学习笔记,略显粗糙,而且也有本人的不成熟的看法在里面,更加细致的内容情况看以下的笔记链接:
https://www.cnblogs.com/xingkongyihao/category/1161554.html?page=2
https://www.cnblogs.com/maxiaodoubao/p/10184428.html
What is machine learning?
在视频里,Andrew Ng就提到不存在一个被广泛认可的定义来准确定义机器学习是什么或不是什么,而在人工智能这个领域其实也有多种学说,这里并不展开讨论,我们回到课程中给出的两种定义。
- Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
这个是一种更久远的定义,Arthur Samuel将其定义为“给予计算机能自我学习的能力而不是编程”
- Tom Mitchell (1998) Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
这一个更新的定义是Tom Mitchell 提出的,“对于某类任务T和性能度量P,如果一个计算机程序在T上以P衡量的性能随着经验E而自我完善,那么我们称这个计算机程序在从经验E学习。”
名称解释:
T:一个专门要实现的目标或任务
P:一个衡量指标,一种表现效果,比如一个硬币出现正面和反面的概率,正面的出现次数是否会随着扔的次数增加而增加。
E:经验E的外在形式其实就是拿到的数据,关于任务T的经验。
不过非常遗憾的是,machine learning的性能在过于庞大的数据面前表现效果并不好,这也说明了一个问题,在机器学习中,数据并不能完全有效转化为机器可以学习到的经验。
根据我本人目前的认知与学习,其实我觉得 Tom Mitchell 的这句话的意思是机器学习到的数据并不是数据本身而是数据的内在规律。
举个简单的例子:你考试考的是对知识的理解和掌握程度而不是背多少题,尽管有些时候背题确实有效,不过换了套卷子,效果可能就不会有多好了,这也是众多高校不肯轻易透露历年考题的重要原因。
另外也许有人会发现,我们往往是通过一张卷子分数来说明一个学生这个阶段的学习效果,而这个分数(特征)本身是由人为设定的,能够衡量学生的学习效果当然还有每天付出的时间、是否坚持锻炼等特征。
专家通过分析哪些“特征”是重要的,然后机器就通过分析历史数据中的这些特征的数据,来找到相应的模式,也就是怎样的特征的组合会导致怎样的结果。
因此机器学习可以有如下两个缺点:
- 在庞大的数据面前,机器学习往往表现效果不佳
- 特征的选择往往被专家把控,而模型的效果与特征往往有极大的关系。
Machine learning algorithms
-
Supervised learning(监督学习)
-
Unsupervised learning(无监督学习)
-
Others: Reinforcement learning, recommender systems.
Week 1 | 1 介绍
第 1 题
对于某类任务T和性能度量P,如果一个计算机程序在T上以P衡量的性能随着经验E而自我完善,那么我们称这个计算机程序在从经验E学习。
假设我们给一个学习算法输入了很多历史天气的数据,让它学会预测天气。什么是P的合理选择?
A. 计算大量历史气象数据的过程
B. 以上都不
C. 正确预测未来日期天气的概率
D. 天气预报任务
题解:
这题选C,这题也是机器学习的定义
第 2 题
假设你正在做天气预报,并使用算法预测明天气温(摄氏度/华氏度),你会把这当作一个分类问题还是一个回归问题?
A. 分类
B. 回归
题解:
选B
第 3 题
假设你在做股市预测。你想预测某家公司是否会在未来7天内宣布破产(通过对之前面临破产风险的类似公司的数据进行训练)。你会把这当作一个分类问题还是一个回归问题?
A. 分类
B. 回归
题解:
这题选A
第 4 题
下面的一些问题最好使用有监督的学习算法来解决,而其他问题则应该使用无监督的学习算法来解决。以下哪一项你会使用监督学习?(选择所有适用的选项)在每种情况下,假设有适当的数据集可供算法学习。
A. 根据一个人的基因(DNA)数据,预测他/她的未来10年患糖尿病的几率
B. 根据心脏病患者的大量医疗记录数据集,尝试了解是否有不同类患者群,我们可以为其量身定制不同的治疗方案
C. 让计算机检查一段音频,并对该音频中是否有人声(即人声歌唱)或是否只有乐器(而没有人声)进行分类
D. 给出1000名医疗患者对实验药物的反应(如治疗效果、副作用等)的数据,发现患者对药物的反应是否有不同的类别或“类型”,如果有,这些类别是什么
题解:
BCD
第 5 题
哪一个是机器学习的合理定义?
A. 机器学习从标记的数据中学习
B. 机器学习能使计算机能够在没有明确编程规则的情况下学习
C. 机器学习是计算机编程的科学
D. 机器学习是允许机器人智能行动的领域
题解:
B,看回上面的两个机器学习的定义
Week 1 | 2 单变量线性回归
第 6 题
基于一个学生在大学一年级的表现,预测他在大学二年级表现。
令x等于学生在大学第一年得到的“A”的个数(包括A-,A和A+成绩)学生在大学第一年得到的成绩。预测y的值:第二年获得的“A”级的数量
这里每一行是一个训练数据。在线性回归中,我们的假设 h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1 x hθ(x)=θ0+θ1x,并且我们使用m来表示训练示例的数量。
| x | y |
|---|---|
| 3 | 2 |
| 1 | 2 |
| 0 | 1 |
| 4 | 3 |
对于上面给出的训练集(注意,此训练集也可以在本测验的其他问题中引用),m的值是多少?
题解:
m=4
第 7 题
对于这个问题,假设我们使用第一题中的训练集。并且,我们对代价函数的定义是
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac{1}{2m} \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
求
J ( 0 , 1 ) J(0,1) J(0,1)
题解:
代进去算一下, J ( 0 , 1 ) = 1 2 × 4 ( ( 3 − 2 ) 2 + ( 1 − 2 ) 2 + ( 0 − 1 ) 2 + ( 4 − 3 ) 2 ) = 0.5 J(0,1)=\frac{1}{2\times 4}((3-2)^2+(1-2)^2+(0-1)^2+(4-3)^2)=0.5 J(0,1)=2×41((3−2)2+(1−2)2+(0−1)2+(4−3)2)=0.5
第 8 题
令问题1(指的是第6题的 h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1 x hθ(x)=θ0+θ1x公式)中,线性回归假设的 θ 0 = − 1 , θ 1 = 2 \theta_0=-1,\theta_1=2 θ0=−1,θ1=2,求 h θ ( 6 ) h_\theta(6) hθ(6)?
题解:
这里也是代进去算一下 h θ ( 6 ) = − 1 + 2 × 6 = 11 h_\theta(6)=-1+2 \times 6 =11 hθ(6)=−1+2×6=11
第 9 题
代价函数 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)与 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1的关系如图2所示。“图1”中给出了相同代价函数的等高线图。根据图示,选择正确的选项(选出所有正确项)
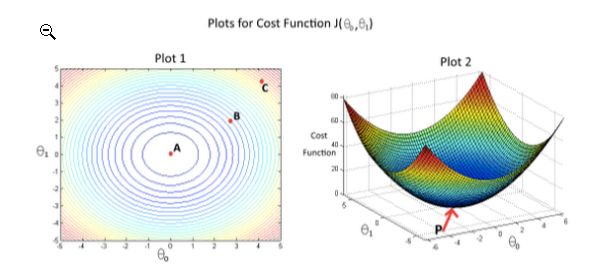
A. 从B点开始,学习率合适的梯度下降算法会最终帮助我们到达或者接近A点,即代价函数在A点有最小值
B. 点P(图2的全局最小值)对应于图1的点C
C. 从B点开始,学习率合适的梯度下降算法会最终帮助我们到达或者接近C点,即代价函数在C点有最小值
D. 从B点开始,学习率合适的梯度下降算法会最终帮助我们到达或者接近A点,即代价函数在A点有最大值
E. 点P(图2的全局最小值)对应于图1的点A
题解:
P是全局最小值,对应的是A,选择则A,E
第 10 题
假设对于某个线性回归问题(比如预测房价),我们有一些训练集,对于我们的训练集,我们能够找到一些 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1,使得 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0。
以下哪项陈述是正确的?(选出所有正确项)
A. 为了实现这一点,我们必须有 θ 0 = 0 , θ 1 = 0 \theta_0=0,\theta_1=0 θ0=0,θ1=0,这样才能使 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0
B. 对于满足 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0的 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1的值,其对于每个训练例子 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)),都有 h θ ( x ( i ) ) = y ( i ) h_\theta(x^{(i)})=y^{(i)} hθ(x(i))=y(i)
C. 这是不可能的:通过 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0的定义,不可能存在 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1使得 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0
D. 即使对于我们还没有看到的新例子,我们也可以完美地预测 y y y的值(例如,我们可以完美地预测我们尚未见过的新房的价格)
题解:
A: 当 θ 0 = 0 , θ 1 = 0 \theta_0=0,\theta_1=0 θ0=0,θ1=0, h θ ( x ) = 0 h_\theta(x)=0 hθ(x)=0,这并不等于 J ( θ 0 , θ 1 ) = 0 J(\theta_0,\theta_1)=0 J(θ0,θ1)=0
B: 当完全拟合时,就会出现损失函数为0的情况,正确
C: B与C说法正好相反. 当完全拟合时,就会出现损失函数为0的情况,我们不排除有这种特例
D: 都没测试就说可以预测,这是扯
Week 1 | 3 线性代数
第 11 题
定义2个矩阵
A = [ 4 3 6 9 ] , B = [ − 2 9 − 5 2 ] A= \begin{bmatrix} 4 & 3 \\ 6 & 9\\ \end{bmatrix},B=\begin{bmatrix} -2 & 9 \\ -5 & 2\\ \end{bmatrix} A=[4639],B=[−2−592]
那么A-B是多少?
A. [ 4 12 1 1 ] \begin{bmatrix} 4 & 12 \\ 1 & 1\\ \end{bmatrix} [41121]
B. [ 6 − 12 11 11 ] \begin{bmatrix} 6 & -12 \\ 11 & 11\\ \end{bmatrix} [611−1211]
C. [ 2 − 6 1 7 ] \begin{bmatrix} 2 & -6 \\ 1 & 7\\ \end{bmatrix} [21−67]
D. [ 6 − 6 11 7 ] \begin{bmatrix} 6 & -6 \\ 11 & 7\\ \end{bmatrix} [611−67]
题解:
很明显这题是D
第 12 题
令
x = [ 2 7 4 1 ] x=\begin{bmatrix} 2 \\ 7\\4 \\ 1\\ \end{bmatrix} x=⎣⎢⎢⎡2741⎦⎥⎥⎤
那么 1 2 ∗ x \frac{1}{2} \ast x 21∗x是多少
题解:
这题的解为
[ 1 7 2 2 1 2 ] \begin{bmatrix} 1 \\ \frac{7}{2}\\2 \\ \frac{1}{2}\\ \end{bmatrix} ⎣⎢⎢⎡127221⎦⎥⎥⎤
第 13 题
令 u u u是一个3维向量,并且
u = [ 5 1 9 ] u=\begin{bmatrix} 5 \\ 1 \\ 9\\ \end{bmatrix} u=⎣⎡519⎦⎤
那么 u T u^T uT是多少
题解:
就是转置的意思,结果为 u T = [ 5 1 9 ] u^T=\begin{bmatrix} 5 & 1 & 9 \end{bmatrix} uT=[519]
第 14 题
令 u , v u,v u,v为3维向量,并且
u = [ 1 2 − 1 ] , v = [ 2 2 4 ] u=\begin{bmatrix} 1 \\ 2\\-1\\ \end{bmatrix},v=\begin{bmatrix} 2 \\ 2\\4\\ \end{bmatrix} u=⎣⎡12−1⎦⎤,v=⎣⎡224⎦⎤
那么 u T v u^Tv uTv是多少?
题解:
[ 1 2 − 1 ] \begin{bmatrix} 1 & 2&-1 \end{bmatrix} [12−1] [ 2 2 4 ] = 1 × 2 + 2 × 2 − 1 × 4 = 2 \begin{bmatrix} 2 \\ 2\\4\\ \end{bmatrix}=1 \times 2 + 2 \times 2 -1 \times 4 =2 ⎣⎡224⎦⎤=1×2+2×2−1×4=2
第 15 题
令A和B是3x3矩阵,以下哪一项一定是正确的(选出所有正确项)
A. A + B = B + A A+B=B+A A+B=B+A
B. 如果 v v v是一个3维向量,那么 A ∗ B ∗ v A \ast B \ast v A∗B∗v是三维向量
C. A ∗ B ∗ A = B ∗ A ∗ B A \ast B \ast A = B\ast A\ast B A∗B∗A=B∗A∗B
D. 如果 C = A ∗ B C = A \ast B C=A∗B,那么是个 6 × 6 6 \times 6 6×6矩阵
题解:
A.很明显是对的
B. A ∗ B A\ast B A∗B得出的本身就为三维的结果,再乘 v v v,最终结果也会变成3维
C.如果学过线性代数,应该很清楚
D.维度还是会为3维
Week 2
Week 2 | 1 多元线性回归
第 16 题
假设m=4个学生上了一节课,有期中考试和期末考试。你已经收集了他们在两次考试中的分数数据集,如下所示:
| 期中得分 | ( 期 中 得 分 ) 2 (期中得分)^2 (期中得分)2 | 期末得分 |
|---|---|---|
| 89 | 7921 | 96 |
| 72 | 5184 | 74 |
| 94 | 8836 | 87 |
| 69 | 4761 | 78 |
你想用多项式回归来预测一个学生的期中考试成绩。具体地说,假设你想拟合一个 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2 hθ(x)=θ0+θ1x1+θ2x2的模型,其中 x 1 x_1 x1是期中得分, x 2 x_2 x2是 ( 期 中 得 分 ) 2 (期中得分)^2 (期中得分)2。此外,你计划同时使用特征缩放(除以特征的“最大值-最小值”或范围)和均值归一化。
标准化后 x 2 ( 4 ) x_2^{(4)} x2(4)的特征值是多少?(提示:期中=89,期末=96是训练示例1)
题解:
参考链接:https://www.jianshu.com/p/ef3534ddda15
我们可以将均值归一化理解为特征缩放的另一种方法。特征缩放和均值归一化的作用都是为了减小样本数据的波动使得梯度下降能够更快速的寻找到一条‘捷径’,从而到达全局最小值。
因此,均值归一化则是先求得所有样本的均值 u u u,从而通过如下两个例子公式或者其他公式
n o r m = x 0 − u x m a x n o r m = x 0 − u x m a x − x m i n 其 中 x 0 是 选 取 的 原 始 输 入 , x m a x 与 x m i n 分 别 是 原 始 输 入 的 最 大 值 与 最 小 值 \begin{aligned} &norm=\frac{x_0-u}{x_{max}}\\ &norm=\frac{x_0-u}{x_{max}-x{min}}\\ &其中x_{0}是选取的原始输入,\\ &x_{max}与x_{min}分别是原始输入的最大值与最小值\\ \end{aligned} norm=xmaxx0−unorm=xmax−xminx0−u其中x0是选取的原始输入,xmax与xmin分别是原始输入的最大值与最小值
使得样本数据在更小的范围内变化同样明显。在分母中,我们可以使用样本的 x m a x x_{max} xmax或者 x m a x − x m i n x_{max}-x_{min} xmax−xmin,根据自身需求,选择最合适的归一化方法。
标准化后 x 2 ( 4 ) x_2^{(4)} x2(4)的意思也就是求 ( 期 中 得 分 ) 2 (期中得分)^2 (期中得分)2第4个数据的第2个特征的归一化值。
∵ u = 7921 + 5184 + 8836 + 4761 4 = 6675.5 ∵ x m a x − x m i n = 8836 − 4761 = 4075 ∵ x 2 ( 4 ) = 4761 ∴ a n s w e r = 4761 − 6675.5 4075 = − 0.47 \begin{aligned} &\because u=\frac{7921+5184+8836+4761}{4}=6675.5\\ &\because x_{max}-x_{min}=8836-4761=4075\\ &\because x_2^{(4)}=4761\\ &\therefore answer=\frac{4761-6675.5}{4075}=-0.47\\ \end{aligned} ∵u=47921+5184+8836+4761=6675.5∵xmax−xmin=8836−4761=4075∵x2(4)=4761∴answer=40754761−6675.5=−0.47
第 17 题
用 α = 0.3 \alpha =0.3 α=0.3进行 15 15 15次梯度下降迭代,每次迭代后计算 J ( θ ) J(\theta) J(θ)。你会发现 J ( θ ) J(\theta) J(θ)的值下降缓慢,并且在 15 15 15次迭代后仍在下降。基于此,以下哪个结论似乎最可信?
A. 是 α = 0.3 \alpha =0.3 α=0.3学习率的有效选择。
B. 与其使用 α \alpha α当前值,不如尝试更小的 α \alpha α值(比如 α = 0.1 \alpha =0.1 α=0.1)
C. 与其使用 α \alpha α当前值,不如尝试更大的 α \alpha α值(比如 α = 1.0 \alpha =1.0 α=1.0)
题解:
三种情况:
-
梯度依旧在下降,尽管它变得缓慢,那么说明代价函数 J ( θ ) J(\theta) J(θ)并未收敛完,表明了 α \alpha α应该要往大点选,我们希望它更快的下降直至平缓。
-
梯度在随着时间上升的话,那么说明代价函数 J ( θ ) J(\theta) J(θ)选的不合理,表明了 α \alpha α应该要往小点选,我们希望它可以下降,最好能够最终迭代到平缓。
-
梯度在随着时间快速下降并直至平缓的话,那么说明代价函数 J ( θ ) J(\theta) J(θ)合理,表明了 α \alpha α是有效选择,我们没必要改变它了。
所以这题应该要选什么?
第 18 题
假设您有 m = 14 m=14 m=14个训练示例,有 n = 3 n=3 n=3个特性(不包括需要另外添加的恒为 1 1 1的截距项),正规方程是 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy。对于给定 m m m和 n n n的值,这个方程中 θ , X , y \theta,X,y θ,X,y的维数分别是多少?
A . X 14 × 3 , y 14 × 1 , θ 3 × 3 B . X 14 × 4 , y 14 × 1 , θ 4 × 1 C . X 14 × 3 , y 14 × 1 , θ 3 × 1 D . X 14 × 4 , y 14 × 4 , θ 4 × 4 \begin{aligned} &A.X \quad 14×3,y \quad 14×1,\theta \quad 3×3 \\ &B.X \quad 14×4,y \quad 14×1,\theta \quad 4×1 \\ &C.X \quad 14×3,y \quad 14×1,\theta \quad 3×1 \\ &D.X \quad 14×4,y \quad 14×4,\theta \quad 4×4 \\ \end{aligned} A.X14×3,y14×1,θ3×3B.X14×4,y14×1,θ4×1C.X14×3,y14×1,θ3×1D.X14×4,y14×4,θ4×4
题解:
X 要 包 括 b i a s , 所 以 是 14 × 4 , y 则 只 用 b i a s , 所 以 为 14 × 1 , θ 则 根 据 上 式 变 成 4 × 1 X要包括bias,所以是14×4,y则只用bias,所以为14 \times 1,\theta则根据上式变成4×1 X要包括bias,所以是14×4,y则只用bias,所以为14×1,θ则根据上式变成4×1
第 19 题
假设您有一个数据集,每个示例有 m = 1000000 m=1000000 m=1000000个示例和 n = 200000 n=200000 n=200000个特性。你想用多元线性回归来拟合参数 θ \theta θ到我们的数据。你更应该用梯度下降还是正规方程?
A. 梯度下降,因为正规方程中 θ = ( X T X ) − 1 \theta=(X^TX)^{-1} θ=(XTX)−1中计算非常慢
B. 正规方程,因为它提供了一种直接求解的有效方法
C. 梯度下降,因为它总是收敛到最优 θ \theta θ
D. 正规方程,因为梯度下降可能无法找到最优 θ \theta θ
题解:
由于 n = 20 W n = 20W n=20W 数量很大,用正规方程的话非常的耗时间
第20题
以下哪些是使用特征缩放的原因?
A. 它可以防止梯度下降陷入局部最优
B. 它通过降低梯度下降的每次迭代的计算成本来加速梯度下降
C. 它通过减少迭代次数来获得一个好的解,从而加快了梯度下降的速度
D. 它防止矩阵 X T X X^TX XTX(用于正规方程)不可逆(奇异/退化)
题解:
特征收缩是减少了迭代次数,加快了得到正确答案的速度,如果不理解,可以看一下吴恩达的课程,也可以看一下《百面机器学习》。
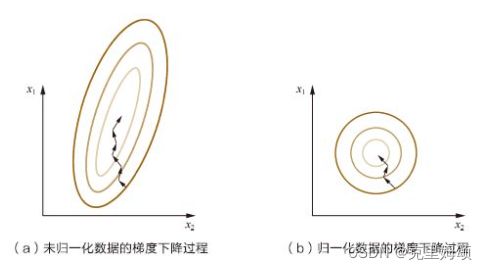
当我们使用了特征缩放,梯度下降的形状就会从原来的椭圆偏向圆形,到达最低点的距离就会减少,相应的表示就是迭代次数减少。
Week 6
视频链接:
https://www.bilibili.com/video/BV164411b7dx?p=65
参考笔记:
https://www.cnblogs.com/xingkongyihao/p/8435691.html
https://www.cnblogs.com/maxiaodoubao/p/10151687.html
课程总结
如果我们遇到了一个需要提升精确度的例子时,我们可以通过误差分析(Error analysis)查看出现误差的原因是否具有某些系统化的规律,通过这些规律来研究和改进我们的算法。
在分类算法例子中,吴恩达引入了查准率(Precision)和查全率(Recall)的概念,将算法预测的结果分为四种情况,而查准率和召回率在逻辑回归问题中会受到我们设置的闸值影响。
一般我们在遇到查准率和召回率作为遇到偏斜类问题的评估度量值中,我们总是希望可以令查准率和召回率可以相对平衡,而后可以通过F1公式求解出的数值来判断我们的闸值是否设置合理。
最后对于机器学习而已,我们通常可以选择很多不同的算法进行预测,随着训练集规模增大,Accuracy一般会提高(因此从来都没有最好的算法,只有最合适的算法),但事实上, 如果数据集中含的有效的特征信息很少时,单纯增大数据集并不能解决一切问题,所以当我们遇到:
- 偏差bias大的情况:增加特征以确保有多参数(对神经网络增加hidden units)
- 方差variance大的情况:增大数据的训练集,使得 J c v J_{cv} Jcv ≈ J t r a i n J_{train} Jtrain ,从而降低过拟合。
参考链接:
- https://www.cnblogs.com/xingkongyihao/p/8432274.html
- https://www.heywhale.com/mw/project/5e0f01282823a10036b280a7