【优化方法学习笔记】第四章:多目标规划
本章目录
- 1. 多目标规划的基本概念
-
- 1.1 向量序
- 1.2 多目标规划
- 1.3 多目标规划的解
- 2. 线性加权和法
- 3. 平方加权和法
- 4. 极小极大法
- 5. 分层序列法
1. 多目标规划的基本概念
1.1 向量序
设 a = ( a 1 , a 2 , ⋯ , a n ) \boldsymbol{a} = (a_1, a_2, \cdots, a_n) a=(a1,a2,⋯,an), b = ( b 1 , b 2 , ⋯ , b n ) \boldsymbol{b} = (b_1, b_2, \cdots, b_n) b=(b1,b2,⋯,bn), 定义:
- 若 ∀ i ∈ { 1 , 2 , ⋯ , n } \forall i \in \lbrace 1,2,\cdots,n \rbrace ∀i∈{1,2,⋯,n}, 都有 a i = b i a_i = b_i ai=bi, 则称向量 a \boldsymbol{a} a等于向量 b \boldsymbol{b} b, 记作 a = b \boldsymbol{a} = \boldsymbol{b} a=b
- 若 ∀ i ∈ { 1 , 2 , ⋯ , n } \forall i \in \lbrace 1,2,\cdots,n \rbrace ∀i∈{1,2,⋯,n}, 都有 a i ≤ b i a_i \le b_i ai≤bi, 则称向量 a \boldsymbol{a} a小于等于向量 b \boldsymbol{b} b, 记作 a ≦ b \boldsymbol{a} \leqq \boldsymbol{b} a≦b
- 若 ∀ i ∈ { 1 , 2 , ⋯ , n } \forall i \in \lbrace 1,2,\cdots,n \rbrace ∀i∈{1,2,⋯,n}, 都有 a i ≤ b i a_i \le b_i ai≤bi, 且 ∃ j ∈ { 1 , 2 , ⋯ , n } \exists j \in \lbrace 1,2,\cdots,n \rbrace ∃j∈{1,2,⋯,n}, 使得 a i < b i a_i < b_i ai<bi, 则称向量 a \boldsymbol{a} a小于向量 b \boldsymbol{b} b, 记作 a ≤ b \boldsymbol{a} \le \boldsymbol{b} a≤b
- 若 ∀ i ∈ { 1 , 2 , ⋯ , n } \forall i \in \lbrace 1,2,\cdots,n \rbrace ∀i∈{1,2,⋯,n}, 都有 a i < b i a_i < b_i ai<bi, 则称向量 a \boldsymbol{a} a严格小于向量 b \boldsymbol{b} b, 记作 a < b \boldsymbol{a} < \boldsymbol{b} a<b
类似可以定义 a ≧ b \boldsymbol{a} \geqq \boldsymbol{b} a≧b, a ≥ b \boldsymbol{a} \ge \boldsymbol{b} a≥b和 a > b \boldsymbol{a} > \boldsymbol{b} a>b。
1.2 多目标规划
目标函数多于一个的优化问题称为多目标规划, 记作(VP), 数学形式为 min x ∈ Ω F ( x ) \underset{\boldsymbol{x} \in \Omega}{\min} \boldsymbol{F}(\boldsymbol{x}) x∈ΩminF(x), 其中 F ( x ) = [ f 1 ( x ) , f 2 ( x ) , ⋯ , f n ( x ) ] T \boldsymbol{F}(\boldsymbol{x}) = \left[ f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), \cdots, f_n(\boldsymbol{x}) \right]^{\rm T} F(x)=[f1(x),f2(x),⋯,fn(x)]T为向量值函数。若 ∀ i ∈ { 1 , 2 , ⋯ , n } \forall i \in \lbrace 1,2,\cdots,n \rbrace ∀i∈{1,2,⋯,n}, f i ( x ) f_i(\boldsymbol{x}) fi(x)都为凸函数, 则称(VP)为凸多目标规划。
1.3 多目标规划的解
设 x ∗ ∈ Ω \boldsymbol{x}^* \in \Omega x∗∈Ω, F ( x ) = [ f 1 ( x ) , f 2 ( x ) , ⋯ , f n ( x ) ] T \boldsymbol{F}(\boldsymbol{x}) = \left[ f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), \cdots, f_n(\boldsymbol{x}) \right]^{\rm T} F(x)=[f1(x),f2(x),⋯,fn(x)]T, (VP)的解有许多种,常用的有:
- 若对 ∀ x ∈ Ω \forall \boldsymbol{x} \in \Omega ∀x∈Ω, 都有 F ( x ∗ ) ≦ F ( x ) \boldsymbol{F}(\boldsymbol{x}^*) \leqq \boldsymbol{F}(\boldsymbol{x}) F(x∗)≦F(x), 则称 x ∗ \boldsymbol{x}^* x∗是(VP)的绝对最优解, 其全体记为 Ω a b \Omega_{\rm ab} Ωab, 有 Ω a b = ⋂ i = 1 n arg min x ∈ Ω f i ( x ) \Omega_{\rm ab} = \bigcap_{i=1}^{n} \underset{\boldsymbol{x} \in \Omega}{\argmin} f_i(\boldsymbol{x}) Ωab=i=1⋂nx∈Ωargminfi(x)
- 若不存在 x ∈ Ω \boldsymbol{x} \in \Omega x∈Ω, 使得 F ( x ∗ ) ≤ F ( x ) \boldsymbol{F}(\boldsymbol{x}^*) \le \boldsymbol{F}(\boldsymbol{x}) F(x∗)≤F(x), 则称 x ∗ \boldsymbol{x}^* x∗是(VP)的有效解(或Pareto解), 其全体记为 Ω p a \Omega_{\rm pa} Ωpa, x ∗ ∈ Ω p a \boldsymbol{x}^* \in \Omega_{\rm pa} x∗∈Ωpa的充要条件是 { F ( x ∗ ) − d ∣ d ≥ 0 } ∩ F ( Ω ) = { F ( x ∗ ) } \lbrace\boldsymbol{F}(\boldsymbol{x^*}) - \boldsymbol{d} \mid \boldsymbol{d} \ge \bold0 \rbrace \cap \boldsymbol{F}(\Omega) = \lbrace \boldsymbol{F}(\boldsymbol{x}^*) \rbrace {F(x∗)−d∣d≥0}∩F(Ω)={F(x∗)}
- 若不存在 x ∈ Ω \boldsymbol{x} \in \Omega x∈Ω, 使得 F ( x ∗ ) < F ( x ) \boldsymbol{F}(\boldsymbol{x}^*) < \boldsymbol{F}(\boldsymbol{x}) F(x∗)<F(x), 则称 x ∗ \boldsymbol{x}^* x∗是(VP)的弱有效解(或弱Pareto解), 其全体记为 Ω w p \Omega_{\rm wp} Ωwp, x ∗ ∈ Ω w p \boldsymbol{x}^* \in \Omega_{\rm wp} x∗∈Ωwp的充要条件是 { F ( x ∗ ) − d ∣ d > 0 } ∩ F ( Ω ) = ∅ \lbrace\boldsymbol{F}(\boldsymbol{x^*}) - \boldsymbol{d} \mid \boldsymbol{d} > \bold0 \rbrace \cap \boldsymbol{F}(\Omega) = \varnothing {F(x∗)−d∣d>0}∩F(Ω)=∅
【例1】求多目标规划的绝对可行解、有效解和弱有效解 min 3 x 1 + x 2 max x 1 + 2 x 2 s . t . x 1 , x 2 ∈ [ 0 , 1 ] \begin{matrix} \min & 3x_1 + x_2 \\ \max & x_1 + 2x_2 \\ \rm s.t. & x_1, x_2 \in [0, 1] \end{matrix} minmaxs.t.3x1+x2x1+2x2x1,x2∈[0,1]【解】 F ( x 1 , x 2 ) = [ f 1 ( x ) , f 2 ( x ) ] T = [ 3 x 1 + x 2 , − x 1 − 2 x 2 ] T \boldsymbol{F}(x_1, x_2) = [f_1(\boldsymbol{x}), f_2(\boldsymbol{x})]^{\rm T} = [3x_1 + x_2, -x_1 - 2x_2]^{\rm T} F(x1,x2)=[f1(x),f2(x)]T=[3x1+x2,−x1−2x2]T, Ω = { ( x 1 , x 2 ) T ∣ x 1 , x 2 ∈ [ 0 , 1 ] } \Omega = \left \lbrace (x_1, x_2)^{\rm T} \mid x_1, x_2 \in [0, 1] \right \rbrace Ω={(x1,x2)T∣x1,x2∈[0,1]}。
显然, 约束优化问题 min x ∈ Ω f 1 ( x ) \underset{\boldsymbol{x} \in \Omega}{\min}f_1(\boldsymbol{x}) x∈Ωminf1(x)的最优解集为 Ω 1 = { ( 0 , 0 ) T } \Omega_1 = \left \lbrace (0, 0)^{\rm T} \right \rbrace Ω1={(0,0)T}, 约束优化问题 min x ∈ Ω f 2 ( x ) \underset{\boldsymbol{x} \in \Omega}{\min}f_2(\boldsymbol{x}) x∈Ωminf2(x)的最优解集为 Ω 2 = { ( 1 , 1 ) T } \Omega_2 = \left \lbrace (1, 1)^{\rm T} \right \rbrace Ω2={(1,1)T}, 所以绝对最优解 Ω a b = Ω 1 ∩ Ω 2 = ∅ \Omega_{\rm ab} = \Omega_1 \cap \Omega_2 = \varnothing Ωab=Ω1∩Ω2=∅。
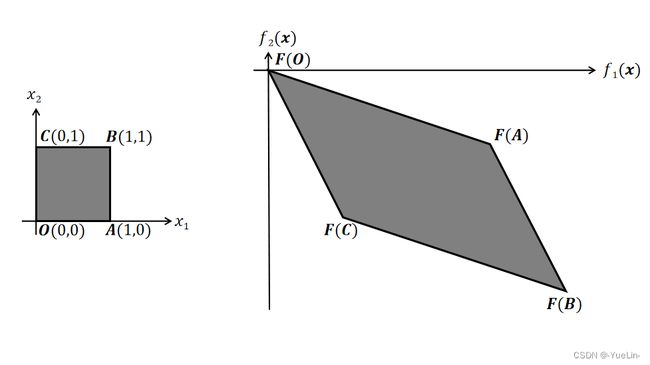
做出可行域 Ω \Omega Ω的图像如图1左图所示, 因 F ( x 1 , x 2 ) \boldsymbol{F}(x_1, x_2) F(x1,x2)是线性函数, 所以把左图中顶点映射后连线即得到像集 F ( Ω ) \boldsymbol{F}(\Omega) F(Ω)的图像, 如图1右图所示。记 O ′ = F ( O ) O' = \boldsymbol{F}(\boldsymbol{O}) O′=F(O), C ′ = F ( C ) C' = \boldsymbol{F}(\boldsymbol{C}) C′=F(C), B ′ = F ( B ) B' = \boldsymbol{F}(\boldsymbol{B}) B′=F(B), 则显然折线段 O ′ C ′ B ′ O'C'B' O′C′B′是有效解, 也是弱有效解。
2. 线性加权和法
线性加权和法对每个目标函数赋予一个权重, 从而把多目标规划转化为单目标规划。具体来说, 对于多目标规划 min x ∈ Ω F ( x ) = [ f 1 ( x ) , f 2 ( x ) , ⋯ , f n ( x ) ] T \underset{\boldsymbol{x} \in \Omega}{\min}\boldsymbol{F}(\boldsymbol{x}) = \left[ f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), \cdots, f_n(\boldsymbol{x}) \right]^{\rm T} x∈ΩminF(x)=[f1(x),f2(x),⋯,fn(x)]T, 给定 n n n个权数 λ 1 , λ 2 , ⋯ , λ n \lambda_1, \lambda_2, \cdots, \lambda_n λ1,λ2,⋯,λn, 则(VP)转化为 min x ∈ Ω ∑ i = 1 n λ i f i ( x ) \underset{\boldsymbol{x} \in \Omega}{\min} \sum_{i=1}^{n}\lambda_if_i(\boldsymbol{x}) x∈Ωmini=1∑nλifi(x)用这种方法得到最优解称为线性加权和意义下的最优解。
线性加权和法求得的解必然是(VP)的有效解, 但不能保证求出所有的有效解。
【例2】取权数 λ 1 = 2 3 \lambda_1=\dfrac{2}{3} λ1=32和 λ 2 = 1 3 \lambda_2=\dfrac{1}{3} λ2=31, 用线性加权和法求解 min f ( x 1 , x 2 ) = ( x 1 , x 2 ) T s . t . x 1 + x 2 ≥ 3 x 1 + x 2 ≤ 5 x 1 ≥ 0 0 ≤ x 2 ≤ 2 \begin{matrix} \min & \boldsymbol{f}(x_1, x_2) = (x_1, x_2)^{\rm T} \\ \rm s.t. & x_1 + x_2 \ge 3 \\ & x_1 + x_2 \le 5 \\ & x_1 \ge 0 \\ & 0 \le x_2 \le 2 \end{matrix} mins.t.f(x1,x2)=(x1,x2)Tx1+x2≥3x1+x2≤5x1≥00≤x2≤2【解】问题转化为 min 2 3 x 1 + 1 3 x 2 s . t . x 1 + x 2 ≥ 3 x 1 + x 2 ≤ 5 x 1 ≥ 0 0 ≤ x 2 ≤ 2 \begin{matrix} \min & \dfrac{2}{3}x_1 + \dfrac{1}{3}x_2 \\ \rm s.t. & x_1 + x_2 \ge 3 \\ & x_1 + x_2 \le 5 \\ & x_1 \ge 0 \\ & 0 \le x_2 \le 2 \end{matrix} mins.t.32x1+31x2x1+x2≥3x1+x2≤5x1≥00≤x2≤2如图2所示, 由图解法易得最优解为 ( x 1 , x 2 ) = ( 1 , 2 ) (x_1, x_2) = (1, 2) (x1,x2)=(1,2), 最优值为 4 3 \dfrac{4}{3} 34。

3. 平方加权和法
平方加权和法与线性加权和法类似, 也是把(VP)转化为单目标规划, 具体步骤是先求出约束优化问题 min x ∈ Ω f i ( x ) \underset{\boldsymbol{x} \in \Omega}{\min}f_i(\boldsymbol{x}) x∈Ωminfi(x)的最优解(或近似最优解) y i y_i yi, 然后给定 n n n个权数 λ 1 , λ 2 , ⋯ , λ n \lambda_1, \lambda_2, \cdots, \lambda_n λ1,λ2,⋯,λn, 则(VP)转化为 min x ∈ Ω ∑ i = 1 n λ i [ f i ( x ) − y i ] 2 \underset{\boldsymbol{x} \in \Omega}{\min} \sum_{i=1}^{n}\lambda_i[f_i(\boldsymbol{x}) - y_i]^2 x∈Ωmini=1∑nλi[fi(x)−yi]2用这种方法得到最优解称为平方加权和意义下的最优解。当权数满足 λ 1 = λ 2 = ⋯ = λ n > 0 \lambda_1 = \lambda_2 = \cdots = \lambda_n > 0 λ1=λ2=⋯=λn>0时, 称为理想点法。
平方加权和法求得的解必然是(VP)的有效解。
4. 极小极大法
极小极大法通过极小化极大函数的方式把(VP)转化为单目标规划: min x ∈ Ω max 1 ≤ i ≤ n f i ( x ) \underset{\boldsymbol{x} \in \Omega}{\min}\underset{1 \le i \le n}{\max} f_i(\boldsymbol{x}) x∈Ωmin1≤i≤nmaxfi(x)用这种方法得到最优解称为极大极小意义下的最优解。
经典的极小极大法求得的解必然是(VP)的弱有效解。
5. 分层序列法
分层序列法通过逐个求解目标函数的方式求得最终的最优解, 算法步骤如下:
- 确定 n n n个目标函数的求解顺序, 不妨取为 f 1 ( x ) , f 2 ( x ) , ⋯ , f n ( x ) f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), \cdots, f_n(\boldsymbol{x}) f1(x),f2(x),⋯,fn(x)
- f o r i = 1 , 2 , ⋯ , n d o \bold{for} \; i = 1, 2, \cdots, n \; \bold{do} fori=1,2,⋯,ndo
- \qquad 求解单目标规划 min x ∈ Ω f i ( x ) \underset{\boldsymbol{x} \in \Omega}{\min}f_i(\boldsymbol{x}) x∈Ωminfi(x)得到最优解 x ∗ \boldsymbol{x}^* x∗
- Ω = Ω ∩ { x ∣ f i ( x ) = f i ( x ∗ ) } \qquad \Omega = \Omega \cap \lbrace \boldsymbol{x} \mid f_i(\boldsymbol{x}) = f_i(\boldsymbol{x}^*) \rbrace Ω=Ω∩{x∣fi(x)=fi(x∗)}
- e n d \bold{end} end
- r e t u r n Ω \bold{return} \; \Omega returnΩ
用这种方法得到最优解称为分层序列意义下的最优解。
分层序列法求得的解必然是(VP)的有效解。
【例3】用分层序列法求解 min ( x 2 , x 1 2 + x 2 2 ) T s . t . x 1 + x 2 − 1 ≤ 0 x 1 − 2 x 2 + 2 ≥ 0 x 2 ≥ 0 \begin{matrix} \min & (x_2, x_1^2 + x_2^2)^{\rm T} \\ \rm s.t. & x_1 + x_2 - 1 \le 0 \\ & x_1 - 2x_2 + 2 \ge 0 \\ & x_2 \ge 0 \end{matrix} mins.t.(x2,x12+x22)Tx1+x2−1≤0x1−2x2+2≥0x2≥0【解】第 1 1 1次迭代, 单目标规划为 min x 2 s . t . x 1 + x 2 − 1 ≤ 0 x 1 − 2 x 2 + 2 ≥ 0 x 2 ≥ 0 \begin{matrix} \min & x_2 \\ \rm s.t. & x_1 + x_2 - 1 \le 0 \\ & x_1 - 2x_2 + 2 \ge 0 \\ & x_2 \ge 0 \end{matrix} mins.t.x2x1+x2−1≤0x1−2x2+2≥0x2≥0显然最优解为 x 2 = 0 x_2 = 0 x2=0;
第 2 2 2次迭代, 单目标规划为 min x 1 2 + x 2 2 s . t . x 1 + x 2 − 1 ≤ 0 x 1 − 2 x 2 + 2 ≥ 0 x 2 = 0 \begin{matrix} \min & x_1^2 + x_2^2 \\ \rm s.t. & x_1 + x_2 - 1 \le 0 \\ & x_1 - 2x_2 + 2 \ge 0 \\ & x_2 = 0 \end{matrix} mins.t.x12+x22x1+x2−1≤0x1−2x2+2≥0x2=0该问题等价于 min x 1 2 s . t . − 2 ≤ x 1 ≤ 1 \begin{matrix} \min & x_1^2 \\ \rm s.t. & -2 \le x_1 \le 1 \end{matrix} mins.t.x12−2≤x1≤1显然最优解为 x 1 = 0 x_1 = 0 x1=0, 所以该问题的最优解为 ( x 1 , x 2 ) = ( 0 , 0 ) (x_1, x_2) = (0, 0) (x1,x2)=(0,0)。
所以原问题的最优解为 ( x 1 , x 2 ) = ( 0 , 0 ) (x_1, x_2) = (0, 0) (x1,x2)=(0,0), 最优值为 ( 0 , 0 ) T (0, 0)^{\rm T} (0,0)T。