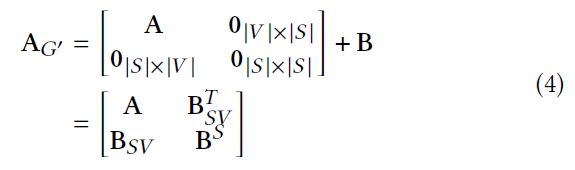【Paper-Attack】Attacking Graph-Based Classification without Changing Existing Connections

Attacking Graph-Based Classification without Changing Existing Connections

背景

training dataset中包含positive node和negative node，positive label代表这个节点是恶意的（fraudulent user），而negative label代表良性（normal user）。

节点分类方法分为两种：

• GNN：抽取图中节点的特征，利用这些特征在节点上做分类任务
• collective classification：基于belief propagation算法，在开始时，根据training dataset为每个节点赋予一个先验信誉分，也为边关联一个权重，然后开始通过加权边来传递先验信誉分，来得到每个节点的后验信誉分。最终collective classification根据计算出的后验信誉分来进行分类。

最近的工作专注于通过增加删除边来修改图的结构，然而这样是有些限制的（删除两个节点之间的边，这两个节点中需要有一个是恶性节点，攻击者无法删除两个良性节点之间的边）

有人研究了在GNN模型上添加新的虚假节点，但是没有人研究基于collective classification方法的这种攻击。

---

攻击者可以插入/创建fake nodes然后把他们和现有的节点连接起来，不修改图中原有的边。

攻击者在原始图中选择一组target node，攻击者的目标是使LinLBP对新加入的fake node和选择的target node（现有的恶意节点）进行错误分类，将本是positive的标记为negative。（在这些节点上提高FNR来逃避检测）

提出一种通过向现有的图中添加虚假节点的基于collective classification的攻击方法Linearized Loopy Belief Propagation(LinLBP)，将新的攻击定义为一个优化问题，并且利用基于梯度的方法来为新添加的节点来生成边。

• 目标函数是创建fake nodes和连接他们与现有节点的总cost。
• 约束条件是fake node与target node的FNR=1
• 每个fake node的solution是决定他是否要与一个现有的节点相连。
• 放松约束条件，近似求解提出的优化问题。（暂时将二进制变量放松为连续变量，并且使用拉格朗日乘法器向目标函数中加入高度非线性的约束）

提出的方法使得全部fake node逃避了检测，并且让LinLBP误分类了大部分的target node。

---

LinLBP

LinLBP为每个节点赋初值

$0<\theta <0.5$

LinLBP用下式计算后验得分

p是后验得分，q是先验得分，W是权重矩阵(0,0.5]，权重越大，连接的两个节点具有相同label的可能性越大

迭代计算后验信誉得分，最终收敛后，$p_u>0$的点是positive的，是恶性节点，值越大，可能性越大。

---

模型

攻击者需要确定执行一次成功攻击所需要的新节点的数量。

假设攻击者已知图数据，且已知positive node和negative node，攻击者选取一组positive node作为target node，目标是让LinLBP将新的fake node 和target node第分类为negative。

新的fake node连接两种节点：

• target node
• 图中剩余节点

---

无向图

$B_{uv}$代表是否在fake node u和节点v之间添加一条边（v可以是现有节点，也可以是fake node）

定义对抗矩阵B

新图G’的邻接矩阵$A_{G^{\prime }}$和$W_{G^{\prime }}$为：

将优化问题定义为：（连接和插入的cost）

**目标：**找到最小化目标函数的对抗矩阵B

由于变量是二进制的，一些约束也是非线性的，所以将二进制变量$B_{uv}$放松为一个连续变量，在解决了有关优化问题之后再转换为二进制。

将第一和第二条约束条件FNR=1修改为$p_u<0$，使用拉格朗日乘法器，将转换后的约束条件加到目标函数中：

利用LinLBP迭代计算后验信誉得分：

---

我们通过利用每一行$b_u^{(t)}$的梯度来搜索$B^{(t)}$的最优质的，即逐个找到每个新的fake node的最优连接。

朝着使得目标函数最小化的反方向移动，$b_u^{(t)}$被初始化为全0，为新fake node u计算连接：

$\lambda$是步长。

由于限制了每个新fake node可以连接的邻居的最大数量K，所以，可以选择$b_u^{(t)}$中的非负的最大的topK个，将他们转换为1，其他的转换为0。