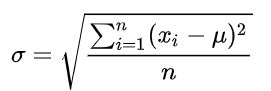python数据分析学习day03:切片索引和统计函数
1. 切片索引
1.1 切片和索引
ndarray对象的内容可以通过索引或切片来访问和修改,与 Python 中 list 的切片操作一样。
ndarray 数组可以基于 0 - n 的下标进行索引。
注意:python list 切片操作后赋值,修改不会改变原数组的值,而numpy数组切片是原始数组视图(这就意味着,如果做任何修改,原始都会跟着更改)。这也意味着,如果不想更改原始数组,我们需要进行显式的复制,从而得到它的副本(.copy())。
np数组索引及切片的值更改会修改原数组
# 可以使用复制操作
ar = np.arange(10)
b = ar.copy()
# 或者 b = np.array(ar)1.2 一维数组
ar1 = np.arange(10) # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# 从索引 2 开始到索引 7 停止,间隔为 2
ar2 = ar1[2:7:2] # array([2, 4, 6])冒号的解释:如果只放置一个参数,
- 如 [2],将返回与该索引相对应的单个元素。
- 如果为 [2:],表示从该索引开始以后的所有项都将被提取。
- 如果为[:7],表示从索引0开始到索引7结束(不包括索引7)
- 如果使用了两个参数,如 [2:7],那么则提取两个索引(不包括停止索引)之间的项。
ar3 = np.arange(1,20,2) # array([ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19])
# 从索引2开始,取后面所有数据
ar3[2:] # array([ 5, 7, 9, 11, 13, 15, 17, 19])
# 从索引2开始到索引7(不包含索引7)
ar3[2:7] # array([ 5, 7, 9, 11, 13])
ar3[:-2] # array([ 1, 3, 5, 7, 9, 11, 13, 15])
# 取所有数据,步长-1,
ar3[::-1] # array([19, 17, 15, 13, 11, 9, 7, 5, 3, 1])
# 取数据1到17之间, 并且间隔一位的数据
ar3[1:-2:2] # array([3, 7, 11, 15])为什么切片和区间会忽略最后一个元素
计算机科学家edsger w.dijkstra(艾兹格·W·迪科斯彻),delattr这一风格的解释应该是比较好的:
- 当只有最后一个位置信息时,我们可以快速看出切片和区间里有几个元素:range(3)和my_list[:3]
- 当起始、终止位置信息都可见时,我们可以快速计算出切片和区间的长度,用(stop-start)即可
- 这样做也让我们可以利用任意一个下标把序列分割成不重叠的两部分,只要写成my_list[:x]和my_list[x:]就可以了。
ar = np.array([10,20,30,40,50,60])
# 在下标2的地方开始分割
print('ar[2:]',ar[2:]) # [30 40 50 60]
# 在下标3的之前结束分割
print('ar[:3]',ar[:3]) # ar[:3] [10 20 30]
# 使用下标2将数组分别为不重叠的两部分
print('ar[:2]',ar[:2]) # ar[:2] [10 20]
print('ar[2:]',ar[2:]) # ar[2:] [30 40 50 60]1.3 二维数组
同样适用上述索引提取方法:
# 定义4行5列的数据
ar4_5 = np.arange(20).reshape(4,5)
ar4_5 #
# 返回ar4_5的秩(几维)
ar4_5.ndim # 2
# 切片为下一维度的一个元素,所以是一维数组
ar4_5[2] # array([10, 11, 12, 13, 14])
# 二次索引取得,一维数组中的元素
ar4_5[2][2] #12
ar4_5[2:] # 取得第3行往后的所有数据
1.4 索引的高级操作
注意:切片还可以使用省略号“…”,如果在行位置使用省略号,那么返回值将包含所有行元素,反之,则包含所有列元素。
# 需要取得第二列数据
ar4_5[...,1] # array([ 1, 6, 11, 16])
#返回第二列后的所有项
ar4_5[...,1:]
# 返回2行3列数据
ar4_5[1,2] # 对应(1,2) 的元素 ar4_5[1][2] == ar4_5[1,2]
# ar4_5[1, 2] 取的是第2行第3列的交叉点
# ar4_5[1][2] 先取第二行,再取第二行的第3列
ar4_5[...][2] # array([10, 11, 12, 13, 14])
# 因为先取所有行,相当于没变,再取第三行在 NumPy 中还可以使用高级索引方式,比如整数数组索引、布尔索引,以下将对两种种索引方式做详细介绍。
整数数组索引
#创建二维数组
x = np.array([
[1, 2],
[3, 4],
[5, 6]
])
#[0,1,2]代表行索引;[0,1,0]代表列索引
y = x[[0,1,2],[0,1,0]]
# y分别获取x中的(0,0)、(1,1) 和(2,0)的数据
y # array([1, 4, 5])获取了 4*3 数组中的四个角上元素,它们对应的行索引是 [0,0] 和 [3,3],列索引是 [0,2] 和 [0,2]。
b = np.array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9,10,11]])
a = b[[0,0,3,3],[0,2,0,2]] # (0,0)(0,2) (3,0) (3,2)
r = np.array([[0,0] ,[3,3]]).reshape(4)
l = np.array([[0,2] ,[0,2]]).reshape(4)
s = b[r,l].reshape((2,2))
'''array([[ 0, 2],
[ 9, 11]])'''a = np.array([
[1,2,3],
[4,5,6],
[7,8,9]
])
# 行取得2行和3行,列取得2列和3列
b = a[1:3, 1:3] # b == a[[1,2],[1,2]]创建一个8x8的国际象棋棋盘矩阵(黑块为0,白块为1)
- [0 1 0 1 0 1 0 1]
- [1 0 1 0 1 0 1 0]
- [0 1 0 1 0 1 0 1]
- [1 0 1 0 1 0 1 0]
- [0 1 0 1 0 1 0 1]
- [1 0 1 0 1 0 1 0]
- [0 1 0 1 0 1 0 1]
- [1 0 1 0 1 0 1 0]]
Z = np.zeros((8, 8), dtype=int)
Z[1::2,::2] = 1
Z[::2,1::2] = 1布尔数组索引
- 筛选出指定区间内数据
- True和False的形式表示需要和不需要的数据
# 返回所有大于6的数字组成的数组
x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
x[x>6] # array([ 7, 8, 9, 10, 11])布尔索引 实现的是通过一维数组中的每个元素的布尔型数值对一个与一维数组有着同样行数或列数的矩阵进行符合匹配。 这种作用,其实是把一维数组中布尔值为True的相应行或列给抽取了出来
x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
x[x%2 == 1] # array([ 1, 3, 5, 7, 9, 11])
x[x%2 == 1] = -1
'''
array([[ 0, -1, 2],
[-1, 4, -1],
[ 6, -1, 8],
[-1, 10, -1]])
'''
# 以上x中大于4并且小于9的数据
x[(x>4) & (x<9)] # array([5, 6, 7, 8])
# 以上x中小于4或者大于9的数据
x[(x<4) | (x>9)] # array([ 0, 1, 2, 3, 10, 11])True和False的形式表示需要和不需要的数据
# 行变量 存在3个元素
row1 = np.array([False,True,True])
# 列变量 存在4个元素
column1 = np.array([True,False,True,False])
# a3_4 是3行, 做切片时也提供3个元素的数组,轴的长度一致
a3_4[row1] # 等价于a3_4[[1,2], :]
'''
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
'''
a3_4[:,column1] # 等价于a3_4[:, [0, 2]]
'''
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
'''
a3_4[row1,column1] # array([ 4, 10]) 等价于a3_4[[1,2],[0,2]]
能够进行切片的前提是:两个一维布尔数组中True的个数需要相等,否则会报错
报错信息如下:indexError: shape mismatch: indexing arrays could not be broadcast together with shapes (2,) (3,)
是因为所选索引形状不匹配:索引数组无法与该形状一起广播。 当访问numpy多维数组时,用于索引的数组需要具有相同的形状(行和列)。numpy将有可能去广播,所以,若要为了实现不同维度的选择, 可分两步对数组进行选择。
- 例如我需要选择第1行和最后一行的第1,3,4列时,先选择行,再选择列。
- 先读取数组 a3_4 的第一行和最后一行,保存到 temp ,然后再筛选相应的列即可。
# 第一步:先选行
temp = a3_4[[0,-1],:]
'''
array([[ 0, 1, 2, 3],
[ 8, 9, 10, 11]])
'''
# 第二步:再选择列
temp[:,[0,2,3]]
'''
array([[ 0, 2, 3],
[ 8, 10, 11]])
'''
# 合并一条
a3_4[[0,-1],:][:,[0,2,3]]但是,如果有一个一维数组长度是1时,这时又不会报错:
# 比如:需要提取第二行,第1,3列的数据
a3_4[[1],[0,2]] # array([4, 6])这里要引出另一个现象:广播 以上相当于(1,0)和(1,2)
2. 广播机制
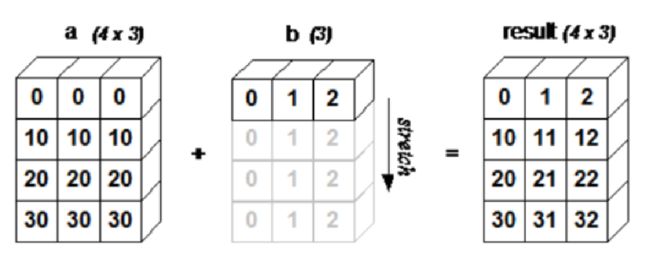
广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式, 对数组的算术运算通常在相应的元素上进行。
如果两个数组 a 和 b 形状相同,即满足 a.shape == b.shape, 那么 a*b 的结果就是 a 与 b 数组对应位相乘。 这要求维数相同,且各维度的长度相同。
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。
4x3 的二维数组与长为 3 的一维数组相加,等效于把数组 b 在二维上重复 4 次再运算
2.1 广播的规则
让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。 如(3) -> (1, 3)
输出数组的形状是输入数组形状的各个维度上的最大值。
如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
M = np.ones((2,3))
print(M)
a = np.arange(3)
print(a)
#两个数组的形状为 M.shape=(2,3),a.shape=(3,)
#可以看到,根据规则1,数组a的维度更小,所以在其左边补1,变为M.shape -> (2,3), a.shape -> (1,3)
#根据规则2,第一个维度不匹配,因此扩展这个维度以匹配数组:M.shape ->(2,3), a.shape -> (2,3)
#现在两个数组的形状匹配了,可以看到它们的最终形状都为(2,3):
M + a
'''
array([[1., 2., 3.],
[1., 2., 3.]])
'''a = np.arange(3).reshape((3,1))
print('a:',a)
b = np.arange(3)
print('b:',b)
a + b
#两个数组的形状为:a.shape=(3,1), b.shape=(3,)
#规则1告诉我们,需要用1将b的形状补全:a.shape -> (3,1), b.shape -> (1,3)
#规则2告诉我们,需要更新这两个数组的维度来相互匹配:a.shape -> (3,3), b.shape -> (3,3)
#因为结果匹配,所以这两个形状是兼容的2.2 对于广播规则另一种简单理解
将两个数组的维度大小右对齐,然后比较对应维度上的数值,如果数值相等或其中有一个为1或者为空,则能进行广播运算。输出的维度大小为取数值大的数值。否则不能进行数组运算
例1:
数组a大小为(2, 3)
数组b大小为(1,)
首先右对齐:
2 3
1
----------
2 3
所以最后两个数组运算的输出大小为:(2, 3)
例2:
数组a大小为(2, 1, 3)
数组b大小为(4, 1)
首先右对齐:
2 1 3
4 1
----------
2 4 3
所以最后两个数组运算的输出大小为:(2, 4, 3)
例3:
数组a大小为(2, 1, 3)
数组b大小为(4, 2)
首先右对齐:
2 1 3
4 2
----------
2跟3不匹配,此时就不能做运算
3. 统计函数
求平均值 mean()
m1 = np.arange(20).reshape((4,5))
# 默认求出数组所有元素的平均值
m1.mean() # 9.5若想求某一维度的平均值,设置 axis 参数,多维数组的元素指定
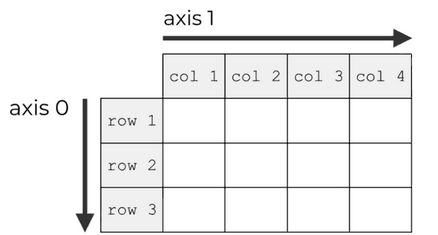
- axis = 0,将从上往下计算
- axis = 1,将从左往右计算
# axis=0将从上往下计算平均值
m1.mean(axis=0) # array([ 7.5, 8.5, 9.5, 10.5, 11.5])
# axis=1 将从左往右计算平均值
m1.mean(axis=1) # array([ 2., 7., 12., 17.])中位数 np.median
又称中点数,中值
是按顺序排列的一组数据中居于中间位置的数,代表一个样本、种群或概率分布中的一个数值
- 平均数:是一个"虚拟"的数,是通过计算得到的,它不是数据中的原始数据。. 中位数:是一个不完全"虚拟"的数。
- 平均数:反映了一组数据的平均大小,常用来一代表数据的总体 "平均水平"。. 中位数:像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的"中等水平"
ar1 = np.array([1,3,5,6,8])
np.median(ar1) # 5.0
ar1 = np.array([1,3,5,6,8,9])
np.median(ar1) # 5.5求标准差 np.std
在概率统计中最常使用作为统计分布程度上的测量,是反映一组数据离散程度最常用的一种量化形式,是表示精确度的重要指标
- 标准差定义是总体各单位标准值与其平均数的差的平方的算术平均数的平方根。
math.sqrt(np.sum(((a - np.mean(a)) ** 2)) / a.size)简单来说,标准差是一组数据平均值分散程度的一种度量。
- 一个较大的标准差,代表大部分数值和其平均值之间差异较大
- 一个较小的标准差,代表这些数值较接近平均值。
'''
例如,A、B两组各有6位学生参加同一次语文测验,
A组的分数为95、85、75、65、55、45,
B组的分数为73、72、71、69、68、67。
分析那组学生之间的差距大?
'''
a = np.array([95,85,75,65,55,45])
b = np.array([73,72,71,69,68,67])
print('A组的标准差为:',a.std()) # A组的标准差为: 17.07825127659933
print('B组的标准差为:',b.std()) # B组的标准差为: 2.160246899469287标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
方差ndarray.var()
衡量随机变量或一组数据时离散程度的度量,方差是标准差的平方
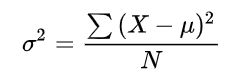
a = np.array([95,85,75,65,55,45])
b = np.array([73,72,71,69,68,67])
print('A组的方差为:',a.var()) # A组的方差为: 291.6666666666667
print('B组的方差为:',b.var()) # B组的方差为: 4.666666666666667标准差有计量单位,而方差无计量单位,但两者的作用一样,虽然能很好的描述数据与均值的偏离程度,但是处理结果是不符合我们的直观思维的。
求最大值 ndarray.max()
print(m1.max()) # 19
print('axis=0,从上往下查找:',m1.max(axis=0)) # axis=0,从上往下查找: [15 16 17 18 19]
print('axis=1,从左往右查找:',m1.max(axis=1)) # axis=1,从左往右查找: [ 4 9 14 19]求最小值 ndarray.min()
print(m1.min()) # 0
print('axis=0,从上往下查找:',m1.min(axis=0)) # axis=0,从上往下查找: [0 1 2 3 4]
print('axis=1,从左往右查找:',m1.min(axis=1)) # axis=1,从左往右查找: [ 0 5 10 15]求和 ndarray.sum()
print(m1.sum()) # 190
print('axis=0,从上往下查找:',m1.sum(axis=0)) # axis=0,从上往下查找: [30 34 38 42 46]
print('axis=1,从左往右查找:',m1.sum(axis=1)) # axis=1,从左往右查找: [10 35 60 85]加权平均值 numpy.average()
即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数
numpy.average(a, axis=None, weights=None, returned=False)
-
weights: 数组,可选
与 a 中的值关联的权重数组。 a 中的每个值都根据其关联的权重对平均值做出贡献。权重数组可以是一维的(在这种情况下,它的长度必须是沿给定轴的 a 的大小)或与 a 具有相同的形状。如果 weights=None,则假定 a 中的所有数据的权重等于 1。一维计算是:
avg = sum(a * weights) / sum(weights)
对权重的唯一限制是 sum(weights) 不能为 0。
average_a1 = [20,30,50]
# 不设置weight 则与平均值一样
print(np.average(average_a1))
print(np.mean(average_a1))
实例1:
我们对比两位学生的考试成绩
| 姓名 | 平时测验 | 期中考试 | 期末考试 |
|---|---|---|---|
| 小明 | 80 | 90 | 95 |
| 小刚 | 95 | 90 | 80 |
学校规定的学科综合成绩的计算方式是:
| 平时测验占比 | 期中考试占比 | 期末考试占比 |
|---|---|---|
| 20% | 30% | 50% |
要求 :比较谁的综合成绩更好
xiaoming = np.array([80,90,95])
xiaogang = np.array([95,90,80])
# 权重:
weights = np.array([0.2,0.3,0.5])
# 分别计算小明和小刚的平均值
print(np.mean(xiaoming)) # 88.33333333333333
print(np.mean(xiaogang)) # 88.33333333333333
# 分别计算小明和小刚的加权平均值
print(np.average(xiaoming, weights=weights)) # 90.5
print(np.average(xiaogang, weights=weights)) # 86.0实例2:
股票价格的波动是股票市场风险的表现,因此股票市场风险分析就是对股票市场价格波动进行分析。波动性代表了未来价格取值的不确定性,这种不确定性一般用方差或标准差来刻画(Markowitz,1952)。
下表是中国和美国部分时段的股票统计指标,其中中国证券市场的数据由“钱龙”软件下载,美国证券市场的数据取自ECI的“WorldStockExchangeDataDisk”。表2股票统计指标
| 年份 | 业绩表现 | 业绩表现 | 波动率 | 波动率 |
|---|---|---|---|---|
| 年代 | [上证综指] | [标准普尔指数] | [上证综指] | [标准普尔指数] |
| 1996 | 110.93 | 16.46 | 0.2376 | 0.0573 |
| 1997 | -0.13 | 31.01 | 0.1188 | 0.0836 |
| 1998 | 8.94 | 26.67 | 0.0565 | 0.0676 |
| 1999 | 17.24 | 19.53 | 0.1512 | 0.0433 |
| 2000 | 43.86 | -10.14 | 0.097 | 0.0421 |
| 2001 | -15.34 | -13.04 | 0.0902 | 0.0732 |
| 2002 | -20.82 | -23.37 | 0.0582 | 0.1091 |
变异系数(Coefficient of Variation):当需要比较两组数据离散程度大小的时候,如果两组数据的测量尺度相差太大,或者数据量纲的不同,直接使用标准差来进行比较不合适,此时就应当消除测量尺度和量纲的影响,而变异系数可以做到这一点,它是原始数据标准差与原始数据平均数的比
# 股票信息
stat_info = np.array([
[110.93, 16.46, 0.2376, 0.0573],
[-0.13, 31.01, 0.1188, 0.0836],
[8.94, 26.67, 0.0565, 0.0676],
[17.24, 19.53, 0.1512, 0.0433],
[43.86, -10.14, 0.097, 0.0421],
[-15.34, 13.04, 0.0902, 0.0732],
[-20.82, 23.37, 0.0582, 0.1091]
])
# 先计算7年的期望值(平均值)
stat_mean = np.mean(stat_info, axis=0)
print(stat_mean) # [20.66857143 17.13428571 0.11564286 0.06802857]
# 计算7年的标准差
stat_std = np.std(stat_info, axis=0)
print(stat_std) # [4.18923479e+01 1.24739349e+01 5.84811046e-02 2.18930983e-02]
# 因为标准差是绝对值,不能通过标准差对中美直接进行对比,而变异系数可以直接比较
# 变异系数 = 原始数据标准差 / 原始数据平均数
stat_std / stat_mean # array([2.02686228, 0.72801021, 0.50570442, 0.32182211])