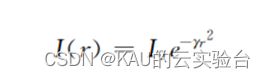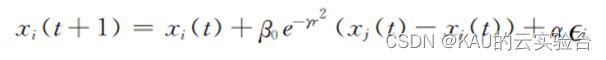超详细 | 萤火虫算法原理及其实现(Matlab)
群智能(Swarm Intelligence,SI)是一类分散自组织系统的集体智能行为的总称,该表述最早在1989年由Gerardo Beni在分子自动机系统中提出。SI系统可视作一组简单的个体,其个体与个体、个体与环境之间存在交互作用,最终表征出智能行为。尽管每个个体遵循及其简单的规则,且整个群体没有中心控制,但最终局部个体之间的交互作用引发了全局层面上智能的涌现。
SI 的研究为学术、工业等实际问题提供了新的解决方法,一些学者根据昆虫群体和其他动物群体的集体行为,提出相应的 SI 优化算法,常见的有蚁群优化、粒子群优化和前面介绍过的灰狼优化算法等,本文中作者将主要介绍SI优化算法之一的萤火虫算法。
萤火虫算法(firefly algorithm,FA)是英国学者Yang于2008年提出的一种元启发式算法[1]该算法通过模拟自然界中萤火虫个体之间相互吸引的理想化行为达到寻优目的,由于操作简单,需要调整的参数少且性能优越,一经提出便受到国内外研究人员的关注,广泛应用于计算机科学、复杂方程求解、结构和工程优化领域。
00 目录
1 萤火虫算法原理
2 代码目录
3 算法性能
4 源码获取
01 萤火虫算法(FA)原理
对萤火虫算法有所了解的同学可能会发现,除了前面卡卡提到的FA外,还有一种版本的萤火虫优化算法(Glowworm swarm optimization,GSO),这是在2005年由印度学者Krishnanand[2]提出的,两者的仿生原理大致相同,但在具体实现上有一定差异,本文将主要介绍FA,在介绍过程中,卡卡也会提到两者的差异所在。
在大自然界中,萤火虫利用自身所发出的光亮作为一种信号去吸引其他个体,而萤火虫只会飞向比自己更明亮的个体。FA 算法即是模拟萤火虫的这种行为而提出的群体智能算法。FA包含两个重要因素,一个是亮度,另一个是吸引力。亮度反映了萤火虫的位置,并决定了萤火虫移动的方向。吸引力决定了萤火虫移动的距离。通过不断更新亮度和吸引力可以实现客观优化。
其核心思想是:低亮的萤火虫被吸引到更明亮的萤火虫,然后它们向更明亮的萤火虫移动,以更新它们的位置。萤火虫的亮度取决于目标函数的适应度值,亮度越高,适应度值越好。如果两个相邻的萤火虫有相同的亮度,萤火虫将随机移动。
FA的数学模型描述如下:
亮度
式中:I0为初始亮度,参数γ代表亮度的损失因素,r为两个萤火虫之间的距离。
吸引力是个体移动机制的重要因素,其中β0为萤火虫之间的最大吸引力,即距离r=0时的两萤火虫之间的吸引力。而在之前许多学者研究表明,式中的γ的取值对该算法的性能有着很大的影响。
式中:rij是萤火虫i、j在解空间中的坐标的笛卡尔距离,d为解空间的总维度。
在算法的演化迭代过程中,当萤火虫xi的亮度小于萤 火虫xj时,萤火虫xi便根据上式进 行移动。在式中,t为算法的迭代次数,xi、xj是两个萤火虫所处解空间的位置。参数α为步长因子,同样其取值对该算法性能也具有较大影响。一般建议设置在(0,1]区间。∈i在[-0.5,0.5],通常是由高斯分布、均匀分布或其它分布生成的随机数向量。
以上是FA的数学模型,
首先,其每个萤火虫与其他每个萤火虫都有交流,而在GSO中,每个萤火虫有其决策域半径,其仅对位于其决策域内的萤火虫起调节作用,这可能会使萤火虫之间协作不足,易陷入局部最优,但这样也能减少其计算复杂度。
其次,FA在移动操作中存在一个扰动项∈i,可以避免其陷入局部最优,而GSO中是移动步长,能够加大其对整个解空间的搜索。
两种算法各有所长,具体细节读者可以自行深入。
PS:其中,萤火虫算法独特的吸引机制也常作为局部扰动引入到其他算法中,即将“移动”操作引入其他算法中作为扰动以提升算法的局部搜索能力。
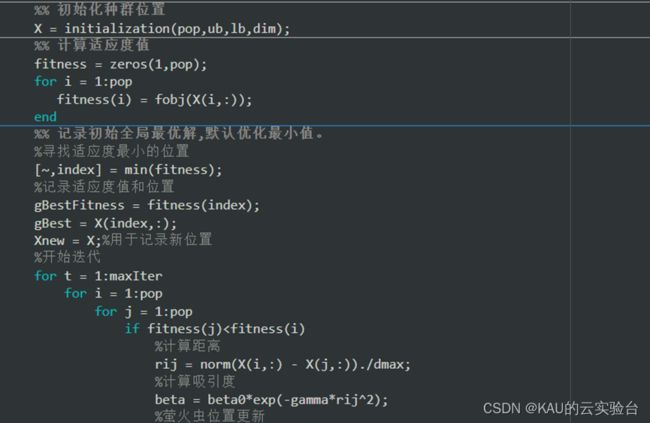
FA算法的实现步骤可表示如下:
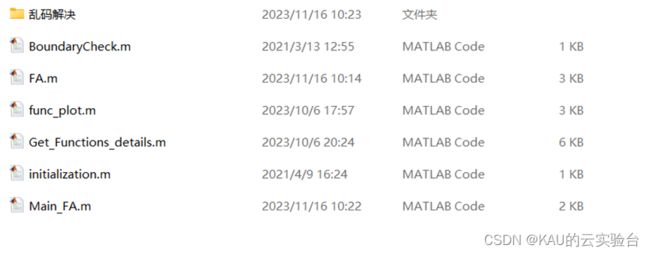
02 代码目录
考虑到很多同学获取代码后有乱码(matlab版本问题),可以将matlab版本改为2020或2021,或使用乱码解决文件夹中的txt文件即可。
03 算法性能
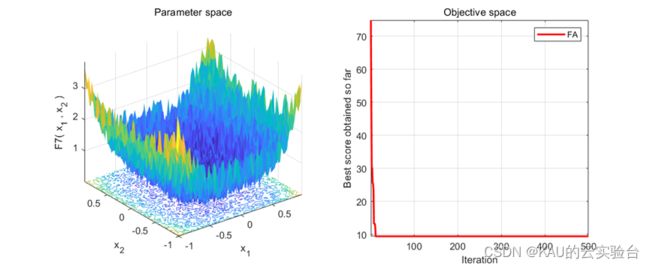
采用标准测试函数初步检验其寻优性能
在MATLAB中执行程序结果如下:
04 源码获取
在作者GZH :KAU的云实验台 回复 FA 即可
由前面对其原理的介绍可以发现,
由于萤火虫都需要与其余的所有萤火虫进行相互吸引,即全互连,这将导致其计算复杂度高,同时可能会引起震荡,影响收敛速度,这可以采用非全互连的结构,如精英交互等;
其次,萤火虫的位置更新主要依据吸引力和扰动步长,这在原算法中是固定的,可以在算法中设置使其动态调整来平衡其在前期和后期的勘探和开发。后续作者也会发布有关FA的原创改进。
参考文献
[1] YANG X S. Nature-inspired metaheuristic algorithms[M]. Frome: Luniver Press,2008.
[2] Krishnanand K N,Ghose D.Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions[J].Swarm Intelligence,2009, 3(2):87-124
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!