二叉树_二叉链表存储_前中后遍历_栈:递归非递归遍历_队列:按层遍历
目录:
1.二叉树的存储结构之二叉链表
1.1以先序序列输入二叉树中结点的值,并构建该二叉树!
2.遍历二叉树
2.1前、中、后序的递归遍历算法
2.2前、中、后序的非递归遍历算法(栈)
2.3按层遍历二叉树(队列)
1.二叉树的存储结构之二叉链表
1.1以先序序列输入二叉树中结点的值,并构建该二叉树!
/*二叉树的结点存储结构,二叉链表存储结构*/
typedef struct BiTNode{
char data;
struct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
/*
BiTNode:是结构类型
BiTree:是指向结点BiTNode的指针类型
*/
bool CreateBiTree(BiTree& T)//指针引用 BiTNode*&,即我要在函数内部改变T的值!T的指向地址值
{/*按先序序列输入二叉树的中结点的值,-表示空树。构造二叉链表表示的二叉树T*/
char ch;
cin >> ch;
if (ch == '-') T = nullptr;
else
{
//if (!(T = (BiTNode*)malloc(sizeof(BiTNode)))) exit(0);
T = new BiTNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
return true;
}
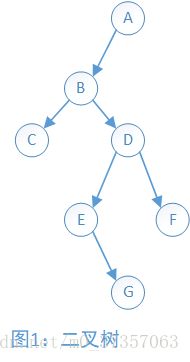
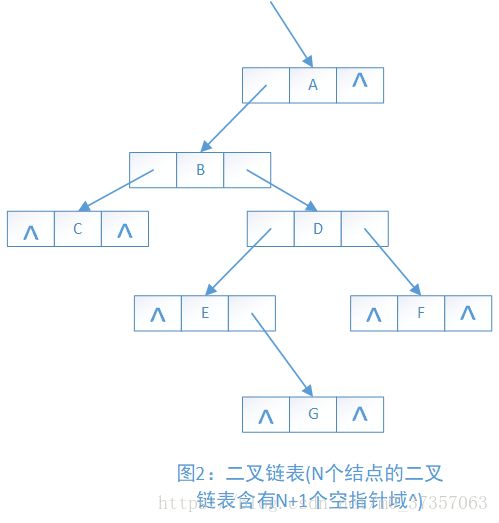
如:输入:A B C - - D E - G - - F - - -
则构造图1的二叉树:
int _tmain(int argc, _TCHAR* argv[])
{
BiTree T=nullptr;
//以二叉列表数据结构存储方式构造二叉树(数据元素为字符char)
CreateBiTree(T);
system("pause");
return 0;
}
输入:A B C - - D E - G - - F - - -
2.遍历二叉树
2.1前、中、后序的递归遍历算法
void PreOrderTraverseRecursive(BiTree T, void(*funcPtr)(BiTree))
{//对采用二叉链表表示的二叉树的先序遍历算法
/*先序遍历二叉树T的递归算法!*/
if (T)
{
funcPtr(T);
PreOrderTraverseRecursive(T->lchild, funcPtr);
PreOrderTraverseRecursive(T->rchild, funcPtr);
}
else
{
return;
}
}
void InOrderTraverseRecursive(BiTree T, void(*funcPtr)(BiTree))
{//对采用二叉链表表示的二叉树的中序遍历算法
/*中序遍历二叉树T的递归算法!*/
if (T)
{
InOrderTraverseRecursive(T->lchild, funcPtr);
funcPtr(T);
InOrderTraverseRecursive(T->rchild, funcPtr);
}
else
{
return;
}
}
void PostOrderTraverseRecursive(BiTree T, void(*funcPtr)(BiTree))
{//对采用二叉链表表示的二叉树的后序遍历算法
/*后序遍历二叉树T的递归算法!*/
if (T)
{
PostOrderTraverseRecursive(T->lchild, funcPtr);
PostOrderTraverseRecursive(T->rchild, funcPtr);
funcPtr(T);
}
else
{
return;
}
}
2.2前、中、后序的非递归遍历算法(栈)
2.2.1前序遍历的非递归算法:以栈模拟递归的过程:
void PreOrderTraverseLoop(BiTree T, void(*funcPtr)(BiTree))
{
stack biTreeStack;
BiTree p;
if (T)
{
biTreeStack.push(T);
while (!biTreeStack.empty())
{
p = biTreeStack.top();
biTreeStack.pop();
if (p)//因为p有可能是某个叶子结点的孩子为空指针。
{
funcPtr(p);
biTreeStack.push(p->rchild);//先把右孩子压入栈
biTreeStack.push(p->lchild);//再把左孩子压入栈
//出栈顺序反之,先出左孩子结点
}
}
}
} 2.2.2中序遍历的非递归算法:以栈模拟递归的过程:
void InOrderTraverseLoopE1(BiTree T, void(*funcPtr)(BiTree))
{
stack biTreeStack;
BiTree p;
if (T)
{
biTreeStack.push(T);
while (!biTreeStack.empty())
{
while ((p = biTreeStack.top()) != nullptr)
{//走到左尽头
biTreeStack.push(p->lchild);
}
biTreeStack.pop();//空指针退栈,因会把叶子节点的左孩子(为空)压进去,要退栈
if (!biTreeStack.empty())
{
/*弹出栈顶元素,并访问该节点,即访问子树的根结点,
最左端的叶子结点可看出其左右子树都为空的子树根结点*/
p = biTreeStack.top();
biTreeStack.pop();
funcPtr(p);
/*然后将其右孩子进栈*/
biTreeStack.push(p->rchild);
}//if循环结束
}//while循环结束
}
else
{
return;
}
} /*E2版本的中序遍历结构更加清晰、易懂!*/
void InOrderTraverseLoopE2(BiTree T, void(*funcPtr)(BiTree))
{/*二叉树T采用二叉链表存储结构,中序遍历T的非递归算法,对每一个元素调用funcPtr函数*/
stack biTreeStack;//存储结点指针的栈
BiTree p;
p = T;
while (p || !biTreeStack.empty())
{
if (p)
{//根指针进栈,然后遍历左子树
biTreeStack.push(p);
p = p->lchild;//这里也是一直走到最下边的结点
}
else
{//根指针退栈,访问根结点,然后遍历右子树
p=biTreeStack.top();
biTreeStack.pop();
funcPtr(p);
p = p->rchild;
}
}
}
2.2.3后序遍历的非递归算法:以栈模拟递归的过程:
/*
二叉树的后序遍历--非递归实现
https://www.cnblogs.com/rain-lei/p/3705680.html
https://www.cnblogs.com/rain-lei/p/3705680.html
leetcode中有这么一道题,非递归来实现二叉树的后序遍历。
二叉树的后序遍历顺序为,root->left, root->right, root,
因此需要保存根节点的状态。显然使用栈来模拟递归的过程,
但是难点是怎么从root->right转换到root。
方法1:判断是否轮到栈顶p访问法,设立刚访问结点指针last
对于节点p可以分情况讨论
1. p如果是叶子节点,直接访问(输出)
2. p如果有孩子,且孩子没有被访问过,则按照右孩子,左孩子的顺序依次入栈
3. p如果有孩子,而且孩子都已经访问过,则访问p节点
如何来表示出p的孩是否都已经访问过了呢?
最暴力的方法就是对每个节点的状态进行保存,
这么做显然是可以的,但是空间复杂度太大了。
我们可以保存最后一个访问的节点last,
如果满足 (p->right==NULL && last ==p->left) || last=p->right,
那么显然p的孩子都访问过了,接下来可以访问p
*/
二叉树的后序遍历法1:区别栈顶结点p是否该访问了之设立刚访问结点指针法
void PostOrderTraverseE1(BiTree T, void(*funcPtr)(BiTree))
{
if (!T)
return;
stack biTreeStack;//存储结点指针的栈
BiTree p = T;
BiTree last = T;
biTreeStack.push(p);
while (!biTreeStack.empty())
{
p = biTreeStack.top();
/*情况1:如果p是叶子结点,其左右子树都为空,则可直接访问p;
情况2:如果满足 (p->right==NULL && last ==p->left) || last=p->right,
那么显然p的孩子都访问过了,接下来可以访问p
如果p的右子树为空,并且p的左子树已经访问过了,即(p->right==NULL && last ==p->left)
那么就可以访问p了
如果p的右子树也访问过了即last=p->right,也可以访问p了
*/
if ((p->lchild == nullptr&&p->rchild == nullptr) || (p->rchild == nullptr&&last == p->lchild) || (last == p->rchild))
{
funcPtr(p);//访问p
last = p;//将刚才访问的结点标记为p
biTreeStack.pop();//p出栈
}
else
{
if (p->rchild)
{//如果右子树非空,则右子树结点进栈
biTreeStack.push(p->rchild);
}
if (p->lchild)
{//如果左子树非空,则左子树结点进栈
biTreeStack.push(p->lchild);
}
}
}
} 二叉树的后序遍历法2:区别栈顶结点p是否该访问了同一个结点两次压入两次弹出法:
/*
法2:每个结点两次压入法
其实我们希望栈中保存的从顶部依次是root->left, root->right, root,
当符合上面提到的条件时,就进行出栈操作。有一种巧妙的方法可以做到,
对于每个节点,都压入两遍,在循环体中,每次弹出一个节点赋给p,
如果p仍然等于栈的头结点,说明p的孩子们还没有被操作过,
应该把它的孩子们加入栈中,否则,访问p。
也就是说,第一次弹出,将p的孩子压入栈中,第二次弹出,访问p。
*/
void PostOrderTraverseE2(BiTree T, void(*funcPtr)(BiTree))
{
if (T == NULL) return;
BiTree p = T;
stack sta;
sta.push(p);
sta.push(p);
while (!sta.empty())
{
p = sta.top();
sta.pop();
if (!sta.empty() && p == sta.top())
{
if (p->rchild) sta.push(p->rchild), sta.push(p->rchild);//C:逗号,运算符
if (p->lchild) sta.push(p->lchild), sta.push(p->lchild);
}
else
{
funcPtr(p);
}
}
}
2.3按层遍历二叉树(队列)
参考[1]《剑指offer第三版》P172:面试题32从上到下打印二叉树
void levelOrderTraverse(BiTree pTreeRoot, void(*p)(BiTree))
{/*二叉树采用二叉列表的结构,pTreeRoot是指向跟结点的指针,p是函数指针
按层遍历该二叉树*/
if (!pTreeRoot)
return;
std::deque dequeTreeNode;
dequeTreeNode.push_back(pTreeRoot);
while (!dequeTreeNode.empty())
{//队列非空时继续循环!
BiTNode* pNode = dequeTreeNode.front();//取得队头结点
dequeTreeNode.pop_front();//弹出队头结点
//cout << pNode->data << " ";
p(pNode);//调用函数指针,打印该结点的值
if (pNode->lchild)
{//如果有左孩子,就将左孩子结点指针进队
dequeTreeNode.push_back(pNode->lchild);
}
if (pNode->rchild)
{//如果有右孩子,就将右孩子结点指针进队
dequeTreeNode.push_back(pNode->rchild);
}
}
}
以上函数的测试例子:
#include "stdafx.h"
#include
#include
#include
using namespace std;
/*二叉树的结点存储结构,二叉链表存储结构*/
typedef struct BiTNode{
char data;
struct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
void printVal(BiTree T)
{
cout << T->data << " ";
}
int _tmain(int argc, _TCHAR* argv[])
{
BiTree T=nullptr;
//以二叉列表数据结构存储方式构造二叉树(数据元素为字符char)
CreateBiTree(T);
//按层遍历二叉树
cout << "按层遍历二叉树:" << endl;
levelOrderTraverse(T, printVal);
cout << endl;
//先序遍历(递归版本)
cout << "先序遍历(递归版本):" << endl;
PreOrderTraverseRecursive(T, printVal);
cout << endl;
//中序遍历(递归版本)
cout << "中序遍历(递归版本):" << endl;
InOrderTraverseRecursive(T, printVal);
cout << endl;
//后序遍历(递归版本)
cout << "后序遍历(递归版本):" << endl;
PostOrderTraverseRecursive(T,printVal);
cout << endl;
//先序遍历(非递归版本)
cout << "先序遍历(非递归版本):" << endl;
PreOrderTraverseLoop(T, printVal);
cout << endl;
//中序遍历(非递归版本1)
cout << "中序遍历(非递归版本1):" << endl;
InOrderTraverseLoopE1(T, printVal);
cout << endl;
//中序遍历(非递归版本2)
cout << "中序遍历(非递归版本2):" << endl;
InOrderTraverseLoopE2(T, printVal);
cout << endl;
//后续遍历(非递归版本1)
cout << "后续遍历(非递归版本1)" << endl;
PostOrderTraverseE1(T, printVal);
cout << endl;
//后续遍历(非递归版本2)
cout << "后续遍历(非递归版本2)" << endl;
PostOrderTraverseE2(T, printVal);
cout << endl;
system("pause");
return 0;
}
/*
输入:
A B C - - D E - G - - F - - -
输出:
按层遍历二叉树:
A B C D E F G
先序遍历(递归版本):
A B C D E G F
中序遍历(递归版本):
C B E G D F A
后序遍历(递归版本):
C G E F D B A
先序遍历(非递归版本):
A B C D E G F
中序遍历(非递归版本1):
C B E G D F A
中序遍历(非递归版本2):
C B E G D F A
后续遍历(非递归版本1)
C G E F D B A
后续遍历(非递归版本2)
C G E F D B A
请按任意键继续. . .
*/ 二叉树_二叉链表存储_前中后遍历_栈:递归非递归遍历_队列:按层遍历
数据结构