一文弄懂二叉树的三种遍历方式

关注公众号【高性能架构探索】，后台回复【pdf】，免费获取计算机必备经典书籍

俗话说：学如逆水行舟,不进则退;心似平原走马,易放难收。这句话对程序员而言，体会更深。这行已经越来越卷了，时刻准备着，。 二叉树，在面试中，已是必备的开胃菜。而在二叉树相关的面试题目中，遍历更是常考题目。本文将从二叉树的遍历角度入手，从递归和非递归角度来分析和讲解二叉树的遍历。

遍历

二叉树的遍历是指从根节点出发，按照某种次序依次访问二叉树中的所有节点，使每个节点被且仅被访问一次。

二叉树的遍历，有先序遍历、中序遍历以及后续遍历三种。

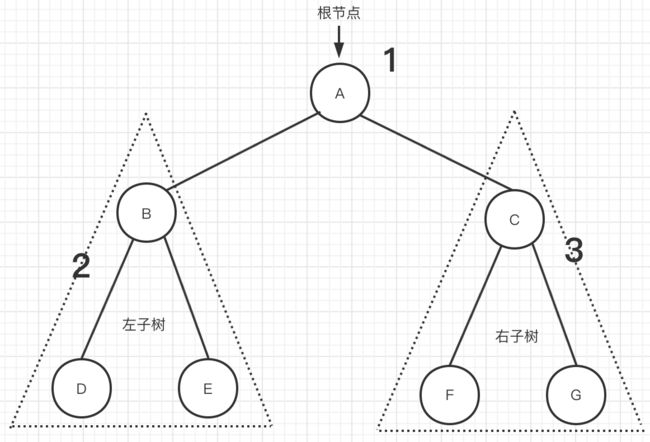
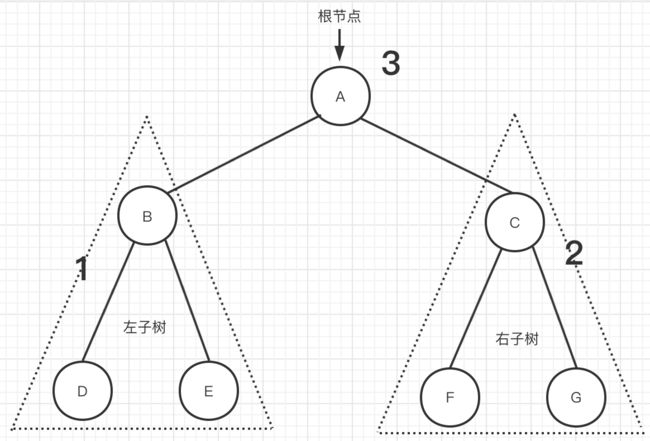
图一

上面三种遍历方式中的先序、中序以及后序三种方式，是父节点相对于子节点来说的。如果父节点先于子节点，那么就是先序遍历。如果子节点先于父节点，那么就是后序遍历。而对于子节点来说，如果先左节点，然后是父节点，然后再是右节点，那么就是中序遍历。

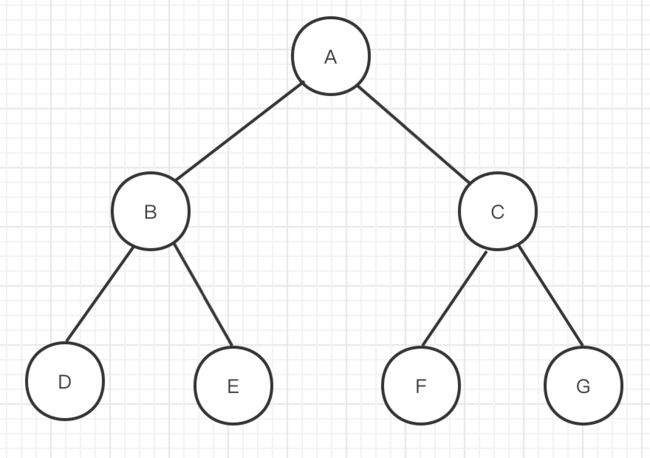
如【图一】所示二叉树。其三种遍历结果如下：

先序遍历: A->B->D->E->C->F->G

中序遍历: D->B->E->A->F->C->G

后续遍历: D->E->B->F->G->C->A

为了便于理解代码，我们先定义下树的节点定义：

struct TreeNode {
  TreeNode *left;
  TreeNode *right;
  int val;
};

先序遍历

定义：先访问父节点，然后遍历左子树，最后遍历右子树。

递归

相信递归遍历大家都会很容易写出来，且bugfree。因为实现代码很简单。

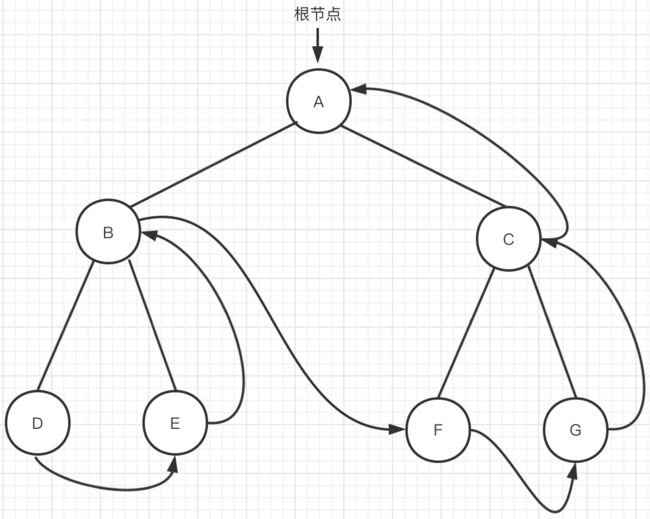
图二 先序遍历

在上图【图二】中，使用递归遍历，就是将其左子树和右子树也当做一棵树来进行处理。代码如下：

void PreOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
   // 遍历根节点(此处仅为输出，读者也可以根据实际需要进行处理，比如存储等)
   std::cout << root->val << std::endl;
   
   // 遍历左子树
   PreOrder(root->left);
   
   // 遍历右子树
   PreOrder(root->right);
}

非递归

在非递归操作中，我们仍然是按照先访问根节点，然后遍历左子树，接着遍历右子树的方式。

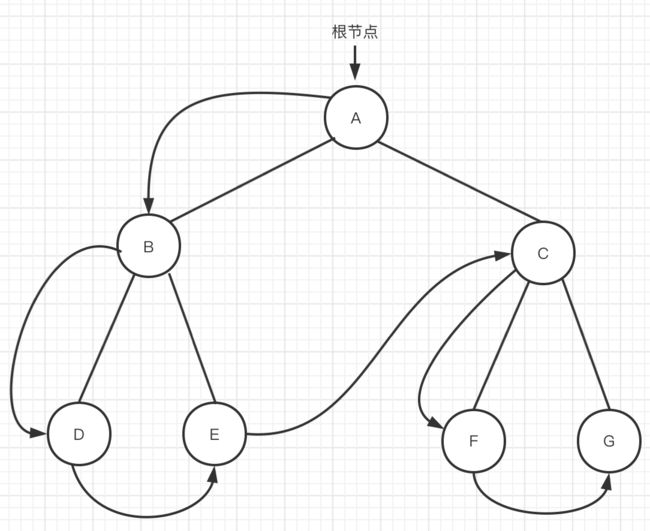
图三 先序遍历

1. 到达节点A,访问节点A,开始遍历A的左子树

2. 到达节点B，访问节点B，开始遍历B的左子树

3. 到达节点D,访问节点D,因为节点D无子树，因此节点D遍历完成

   • 节点D遍历完成，意味着节点B的左子树遍历完成，因此接着遍历节点B的右子树

4. 到达节点E，访问节点E。因为节点E无子树，因此节点E遍历完成

   • 节点E遍历完成，意味着节点B的右子树遍历完成，也预示着节点B的子树遍历完成

   • 开始遍历节点A的右子树

5. 到达节点C，访问节点C。开始遍历C的左子树

6. 到达节点F，访问节点F。因为节点F无子树，因此节点F遍历完成

   • 节点F遍历完成，意味着节点C的左子树遍历完成，因此开始遍历节点C的右子树

7. 到的节点G，访问节点G。因为节点G无子树，因此节点G遍历完成

   • 节点G遍历完成，意味着节点C的右子树遍历完成，进而预示着节点C遍历完成

   • 节点C遍历完成，意味着节点A的右子树遍历完成，进而意味着节点A遍历完成，因此以A为根节点的树遍历完成。

用非递归方式遍历二叉树，需要引入额外的数据结构栈(stack),其基本流程如下： 1、申请一个栈stack，然后将头节点压入stack中。

2、从stack中弹出栈顶节点，打印

3、将其右孩子节点（不为空的话）先压入stack中

4、将其左孩子节点（不为空的话）压入stack中。

5、不断重复步骤2、3、4，直到stack为空，全部过程结束。

代码如下：

void PreOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack s;
  s.push(root); // 步骤1
  
  while (!s.empty()) {
    auto t = s.top();
    s.pop();//出栈
    
    std::cout << t->val << std::endl; // 访问节点
    if (t->right) {
      s.push(t->right); // 对应步骤3
    }
    
    if (t->left) {
      s.push(t->left); // 对应步骤4
    }
  }
}

中序遍历

定义：先遍历左子树，访问根节点，遍历右子树

递归

图四 中序遍历

在上图【图四】中，使用递归遍历，就是将其左子树和右子树也当做一棵树来进行处理。代码如下：

void InOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
  
   
   // 遍历左子树
   InOrder(root->left);
   
    // 遍历根节点(此处仅为输出，读者也可以根据实际需要进行处理，比如存储等)
   std::cout << root->val << std::endl;
   
   // 遍历右子树
   InOrder(root->right);
}

上述中序遍历的递归代码，相比于先序遍历，只是将访问根节点的行为放在了遍历左右子树之间。

非递归

在非递归操作中，我们仍然是按照先遍历左子树，然后访问根节点，最后遍历右子树的方式。

图五 中序遍历

1. 到达节点A，节点A有左子树，遍历节点A的左子树

2. 到达节点B，节点B有左子树，遍历节点B的左子树

3. 到达节点D，节点D无子树，访问D节点

   • 由于D无子树，意味着B的左子树遍历完成，那么就回到B节点

4. 访问B节点，遍历B节点的右子树

5. 到达节点E，节点E无子树，访问节点E

   • E节点遍历完成，意味着以B为根的子树遍历完成，回到A节点

6. 到达A节点，访问A节点，遍历A节点的右子树

7. 到达C节点，遍历C节点的左子树

8. 到达F节点，因为F节点无子树，因此访问F节点。

   • 由于F节点无子树，意味着C节点的左子树遍历完成，回到C节点

9. 到达C节点，访问C节点，遍历C的右子树

10. 到达节点G，由于G无子树，因为访问节点G

• G节点遍历完成，意味着C节点的右子树遍历完成，进而意味着A节点的右子树遍历完成，从意味着以A节点为根的二叉树遍历完成。

中序遍历，同样需要额外的辅助数据结构栈。

1. 将根节点放入栈 2、如果根节点有左子树，则将左子树的根节点放入栈 3、重复步骤1和2.继续遍历左子树 4、从栈中弹出节点，进行访问，然后遍历右子树(重复步骤1和2) 5、如果栈为空，则遍历完成

代码如下：

void InOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack s;
  auto p = root;
  
  while (!s.empty() || p) {
    if (p) { // 步骤1和2
      s.push(p);
      p = p->left;
    } else { // 步骤4
      auto t = s.top();
      std::cout << t->val << std::endl;
      p = t->right;
    }
  }
}

后续遍历

定义：先遍历左子树，再遍历右子树，最后访问根节点

递归

图六 后序遍历

void PostOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
   // 遍历左子树
   PostOrder(root->left);
   
   // 遍历右子树
   PostOrder(root->right);
   
    // 遍历根节点(此处仅为输出，读者也可以根据实际需要进行处理，比如存储等)
   std::cout << root->val << std::endl;
}

上面就是后续遍历的递归写法，比较写先序遍历、中序遍历以及后续遍历三者的递归遍历写法，大部分代码是一样的，唯一的区别就是访问根节点的代码位置不一样：

先序遍历：先访问根节点，然后遍历左子树，最后遍历右子树 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树 后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点

非递归

在非递归操作中，我们仍然是按照先遍历左子树，然后访问根节点，最后遍历右子树的方式。

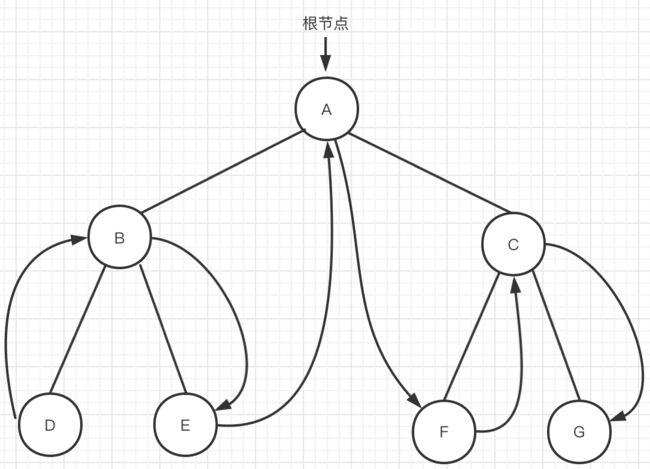
图七 后续遍历

1. 到达节点A，遍历A的左子树

2. 到达节点B，遍历B的左子树

3. 到达节点D，由于D无子树，则访问节点D

   • 节点D无子树，意味着节点B的左子树遍历完成，接着遍历B的右子树

4. 到达节点E，由于E无子树，则访问节点E

   • 节点E无子树，意味着节点B的右子树遍历完成，接回到节点B

5. 访问节点B，回到节点B的根节点A

6. 到达节点A，访问节点A的右子树

7. 到达节点C，遍历节点C的左子树

8. 到达节点F，由于节点F无子树，因此访问节点F

   • 节点F访问完成，意味着C节点的左子树遍历完成，因此回到节点C

9. 到达节点C，遍历节点C的右子树

10. 到达节点G，由于节点G无子树，因为访问节点G

• 节点G访问完成，意味着C节点的右子树遍历完成，回到节点C

1. 到达节点C，访问节点C

• 节点C遍历完成，意味着节点A的右子树遍历完成，回到节点A

1. 节点A的右子树遍历完成，访问节点A

用非递归方式遍历二叉树，需要引入额外的数据结构栈(stack),其基本流程如下： 1、申请两个栈stack，然后将头节点压入指定stack中。

2、从stack中弹出栈顶节点，放入另外一个栈中

3、将其左孩子节点（不为空的话）先压入stack中

4、将其右孩子节点（不为空的话）压入stack中。

5、不断重复步骤2、3、4，直到stack为空。

6、重复访问另外一个栈，直至栈空

void PostOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack s1;
  std::stack s2;
  
  s1.push(root);
  
  while (!s1.empty()) {
    auto t = s1.top();
    s1.pop();
    s2.push(t);
    
    if (t->left) {
      s1.push(t->left);
    }
    
    if (t->right) {
      s1.push(t->right);
    }
  }
  
  while (!s2.empty()) {
    auto t = s2.top();
    s2.pop();
    std::cout << t->val << std::endl;
  }
}

结语

对于二叉树来说，所谓的遍历，是指沿着某条路线依次访问每个节点，且均只做一次访问。二叉树的遍历，是面试中常面算法之一，一定要把其弄懂，必要的时候，需要背诵，乃至做到肌肉记忆。