机器数的定点表示与浮点表示
目录
一、定点表示法
1、定点小数
2、定点整数
二、浮点表示法
1、浮点数的表示范围
2、规格化浮点数
三、浮点数阶码移码的表示
四、浮点数尾数的基数
1、尾数基数大小的选择
2、尾数基数对浮点数特性的影响
五、IEEE754标准浮点数
六、定点、浮点表示法与 定点、浮点计算机
1、定点、浮点表示法范的区别
（1）数值的表示范围额
（2）精度
（3）数的运算
（4）溢出处理
2、定点机与浮点机
（1）定点机
（2）定点机+浮点机
（3）浮点机
计算机在进行算数运算时，需要指出小数点的位置。根据小数点的位置是否固定，在计算机中有两种数据格式：定点表示和浮点表示。
一、定点表示法
在定点表示法中约定：所有数据的小数点位置固定不变。通常，把小数点的位置固定在有效数位的最前面或者末尾，这样就形成了两类定点数。
1、定点小数
定点小数，即纯小数，小数点的位置固定在最高有效数位之前、符号位之后。定点小数的小数点的位置是隐含约定的（即小数点位置不需要存储），小数点并不需要真正地占据一个二进制位。
表示的是符号位，即为0时，代表正数；为1时代表负数。
设机器字长有n+1位，原码定点小数的表示范围为
~
补码定点小数的表示范围-1~
（为什么是-1？1.000…000 反码最大1.111…111 补码最大11.000…000）
对于非纯小数，需要化为定点小数作为定点表示。
2、定点整数
定点整数即纯整数，小数点位置隐含固定在最低有效的数位之后。
设机器字长为n+1位，原码定点整数的表示范围-(2^n-1)~(2^n-1)
补码定点整数的表示范围-2^n~(2^n-1)
在定点表示法中，参加运算的数以及运算结果都必须保证落在该定点数所能表示的数值范围内，如果结果大于最大正整数和最小绝对值最大的负数，统称为“溢出”。这是计算机将暂时中止运算操作，而进行溢出处理
需要说明的是，现代计算机中大多数只采用整数数据表示，小数则通过浮点数表示来实现。
二、浮点表示法
在科学计算中，计算机处理的数往往是混合数，它既有整数部分，也有小数分部，因此计算机中引入了浮点数。
让小数点的位置根据需要而浮动，这就是浮点数。
其中：
- r是浮点数阶码的底，与尾数的基数相同，通常r=2
- E和M都是带符号的定点数，E为阶码，M为尾数
- 在大多数计算机中，尾数M为纯小数，通常由原码或补码来表示；阶码E为纯整数，通常用移码或者补码来表示。
- 浮点数的表示范围由阶码的位数来决定，有效数字的精度主要由尾数的位数来决定
1、浮点数的表示范围
设某浮点数的格式如下，k和n分别表示阶码和尾数的数值位位数，尾数和阶码均用补码来表示
浮点数的一般格式
- 浮点数的底2是隐含的，在整个机器数中不出现。
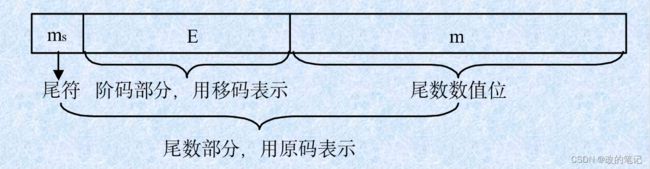
- 阶码的符号位为es，阶码的大小反映了在数N中小数点的实际位置；
- 尾数的符号位为ms，它是整个浮点数的符号位，表示了该浮点数的正负。
当
，
时，阶码和尾数的数值位各位全为1（即阶码和尾数都为最大值）时，该浮点数的最大值为：
但
，是，尾数的最低位
=1，其余为0（即阶码为绝对值最大的负数，尾数为最小整数时），该浮点数的最小正数
当，阶码的数值为全为1；且
，尾数的数值位全0（即阶码为最大正数，尾数为绝对值最大的负数）时，该浮点数为绝对值最大的负数
2、规格化浮点数
为了提高运算的精度，需要充分利用尾数的有效位数位，通常采取浮点数规格化形式，即规定了尾数的最高位数必须是一个有效数值。
规格浮点数的尾数M的绝对值范围：
规格化的最小正数非规格化 的最小正数
非规格化浮点数需要进行规格化才能变成规格化浮点数。所谓的规格化操作就是通过相应的调整一个非规格化浮点数的尾数和阶码的大小，使非零的浮点数在尾数的最高数位上保证时一个有有效数值。
浮点数的典型值
三、浮点数阶码移码的表示
浮点数的阶码是带符号的定点整数
移码就是在真值X基础上加上一个常数，这个常数被称为偏置值，相当于X在数轴上向正方向偏移量若干个单位，移码也称为增码或偏码。
移码的特点：
（1）在移码中，最高位为0表示负数，最高位为1表示正数，与原码、反码、补码的符号位取值相反
（2）移码全为0，他所对应的真值最小；全为1时，多对应的真值最大。（移码的大小可以直观地反映数值的大小）
（3）真值0在移码中的表现形式也是唯一的（真值0在补码中的表现形式是唯一的）
（4）移码把数映射到一个正数阈，所以移码可以视为无符号数
（5）同一数的移码和补码除了最高位相反，其余数相同（偏置置为
时）
阶码采用移码的原因：
（1）便于浮点数大小比较。（阶码大，对应的真值大；阶码小，对应的真值小）
（2）简 机器中的判0电路。（当阶码为0时，尾数全为0）
四、浮点数尾数的基数
1、尾数基数大小的选择
浮点数：
其中 r是阶码的底，同时也是尾数的基数，r的值可为2、4、8、16……（大多数的基数选择为2）
浮点数尾数基数的选择对浮点数的特性起着主要作用，它影响浮点运算的精度，也影响这数值的取值范围，规格化操作是以r为尺度进行移位的，尾数左移或者右移
（以2为基数），阶码将减1或加1.
2、尾数基数对浮点数特性的影响
改变尾数r，会使得浮点数的特性发生以下影响：
（1）可表示数的范围，随着r的增大，可表示数的范围增大
（2）可表示数的个数。随着r的增大，可表示数的个数增加
（3）数在数轴上的分布。随着r的增大，可表示数的精度会减小
（4）运算中精度损失。r愈大，尾数右移的机会就愈小，可降低运算过程中因尾数右移造成的精度损失
（5）运算速度。r增大，将运算中移位的次数减少，运算速度可以提高
五、IEEE754标准浮点数
在目前常用的80*86系列微型计算机中，通常设由支持浮点运算的部件。在这些机器冲的浮点数常常采用IEEE754标准，他和前面介绍的浮点数有些不一样。
| 类型 | 数符 | 阶码 | 尾数数值 | 总位数 | 偏置值 | |
| 十六进制 | 十进制 | |||||
| 短浮点数 | 1 | 8 | 23 | 32 | 7FH | 127 |
| 长浮点数 | 1 | 11 | 52 | 64 | 3FFH | 1023 |
| 临时浮点数 | 1 | 15 | 64 | 80 | 3FFFH | 16383 |
短浮点数又称为单精度浮点数；
长浮点数称为双精度浮点数，他们都采用隐含尾数最高位的方法，这样无形中又增加一位尾数；
临时浮点数又称为扩展精度浮点数，他没有隐含尾数
若是知道了短浮点数，要求其十进制数，将步骤倒退回来就可以了
六、定点、浮点表示法与 定点、浮点计算机
1、定点、浮点表示法范的区别
（1）数值的表示范围额
假设定点数和浮点数的字长相同，浮点表示法所能表示的数值的范围将远远大于定点表示法。
浮点数阶码部分的位数占的越多，可表示的数值范围就越大，但是相应尾数部分的位数将减少，这将使精度下降。因此，阶码和尾数部分各占多少位，必须全面均衡，合理分配。
注意：
不管定点数还是浮点数，每个数值都应于数轴上的一个点。所谓数的范围，实际上指的是数的上、下限，它们之间是一些不连续的点，而不是一段连续的空间
对于定点整数而言，各个点在数轴上的分布是均匀的；而对于浮点数来来说各个点在数轴上的分布是不均匀的，越靠近数轴的原点，两个相邻数之间的距离就愈近。
（2）精度
所谓的精度是指一个数所含有效数值的位数。
一般来说，机器字长越长，它所表示的数的有效位数就越多，精度就越高。对于字长相同的定点数与浮点数来说，浮点数虽然扩大了数的表示范围，但这正式以降低精度为代价的，也就是数轴上各个点的排列更加稀疏了。
（3）数的运算
浮点数包括精度阶码和尾数两个部分，运算时不仅仅要做尾数的运算，还需要做阶码的运算，而且运算结构要求规格化。因此，浮点运算要比定点运算要复杂
（4）溢出处理
在做定点运算时，当运算结果超出数的表的表达范围时，就会发生溢出；
而在浮点运算时，超出尾数的范围时不一定会溢出，只有当阶码也超出表示范围时，才会产生溢出。
2、定点机与浮点机
由于浮点数的运算比较复杂，所以并不是所有的计算机都会浮点运算，通常可将计算机分为以下几类：
（1）定点机
只能处理定点数的计算机称为定点计算机，低档微机和某些专用机大多是定点机，在定点机中机器指令访问的所有操作数都是定点数，如果需要进行浮点运算，则通过软件子程序来实现
（2）定点机+浮点机
浮点运算部件是专门用于对计算机内的附点进行运算的部件，系统配置的附点运算部件使浮点运算速度大大提高。许多微、小型计算机都配有这一部件。
（3）浮点机
具有浮点算运算指令和基本的浮点运算器，通用的大、中计算机多为浮点机。