机器学习-sklearn第十三天——笔记
目录
- 线性回归(下)
-
- 5 非线性问题:多项式回归
-
- 5.1 重塑我们心中的“线性”概念
-
- 5.1.1 变量之间的线性关系
- 5.1.2 数据的线性与非线性
- 5.2 使用分箱处理非线性问题
- 5.3 多项式回归PolynomialFeatures
-
- 5.3.1 多项式对数据做了什么
- 5.3.2 多项式回归处理非线性问题
- 5.3.3 多项式回归的可解释性
- 5.3.4 线性还是非线性模型?
线性回归(下)
5 非线性问题:多项式回归
5.1 重塑我们心中的“线性”概念
在机器学习和统计学中,甚至在我们之前的课程中,我们无数次提到”线性“这个名词。首先我们本周的算法就叫做”线性回归“,而在支持向量机中,我们也曾经提到最初的支持向量机只能够分割线性可分的数据,然后引入了”核函数“来帮助我们分类那些非线性可分的数据。我们也曾经说起过,比如说决策树,支持向量机是”非线性“模型。所有的这些概念,让我们对”线性“这个词非常熟悉,却又非常陌生——因为我们并不知道它的真实含义。在这一小节,我将来为大家重塑线性的概念,并且为大家解决线性回归模型改进的核心之一:帮助线性回归解决非线性问题。
5.1.1 变量之间的线性关系
首先,”线性“这个词用于描述不同事物时有着不同的含义。我们最常使用的线性是指“变量之间的线性关系
5.1.2 数据的线性与非线性
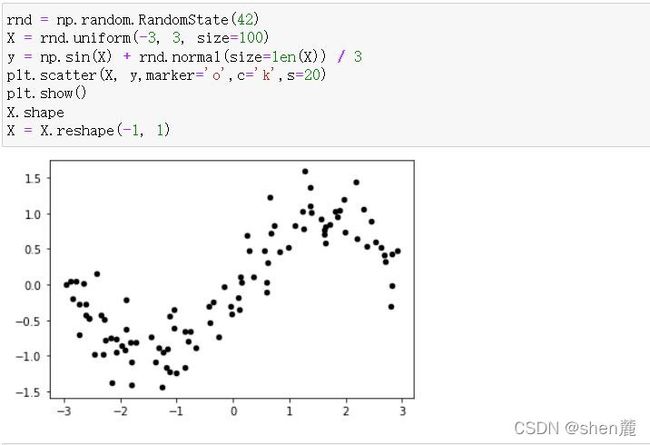
从线性关系这个概念出发,我们有了一种说法叫做“线性数据”。通常来说,一组数据由多个特征和标签组成。当这些特征分别与标签存在线性关系的时候,我们就说这一组数据是线性数据。当特征矩阵中任意一个特征与标签之间的关系需要使用三角函数,指数函数等函数来定义,则我们就说这种数据叫做“非线性数据”。对于线性和非线性数据,最简单的判别方法就是利用模型来帮助我们——如果是做分类则使用逻辑回归,如果做回归则使用线性回归,如果效果好那数据是线性的,效果不好则数据不是线性的。当然,也可以降维后进行绘图,绘制出的图像分布接近一条直线,则数据就是线性的。
对于回归问题,数据若能分布为一条直线,则是线性的,否则是非线性。对于分类问题,数据分布若能使用一条直线来划分类别,则是线性可分的,否则数据则是线性不可分的。
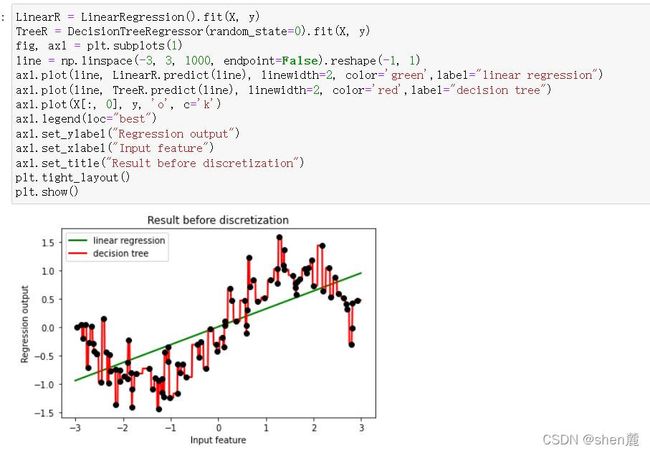
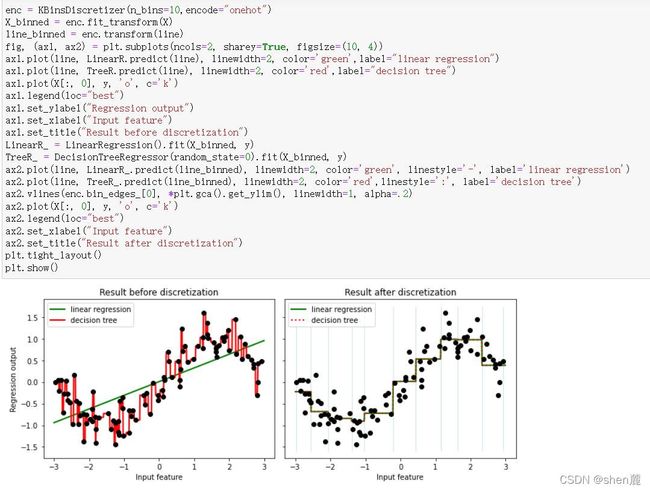
从图像上可以看出,线性回归无法拟合出这条带噪音的正弦曲线的真实面貌,只能够模拟出大概的趋势,而决策树却通过建立复杂的模型将几乎每个点都拟合出来了。可见,使用线性回归模型来拟合非线性数据的效果并不好,而决策树这样的模型却拟合得太细致,但是相比之下,还是决策树的拟合效果更好一些。线性模型用于拟合线性数据,非线性模型用于拟合非线性数据。但事实上机器学习远远比我们想象的灵活得多,线性模型可以用来拟合非线性数据,而非线性模型也可以用来拟合线性数据,更神奇的是,有的算法没有模型也可以处理各类数据,而有的模型可以既可以是线性,也可以是非线性模型!接下来,我们就来一一讨论这些问题。
非线性模型拟合线性数据
非线性模型能够拟合或处理线性数据的例子非常多,我们在之前的课程中多次为大家展示了非线性模型诸如决策树,随机森林等算法在分类中处理线性可分的数据的效果。无一例外的,非线性模型们几乎都可以在线性可分数据上有不逊于线性模型的表现。同样的,如果我们使用随机森林来拟合一条直线,那随机森林毫无疑问会过拟合,因为线性数据对于非线性模型来说太过简单,很容易就把训练集上的 训练得很高,MSE训练的很低。

线性模型拟合非线性数据
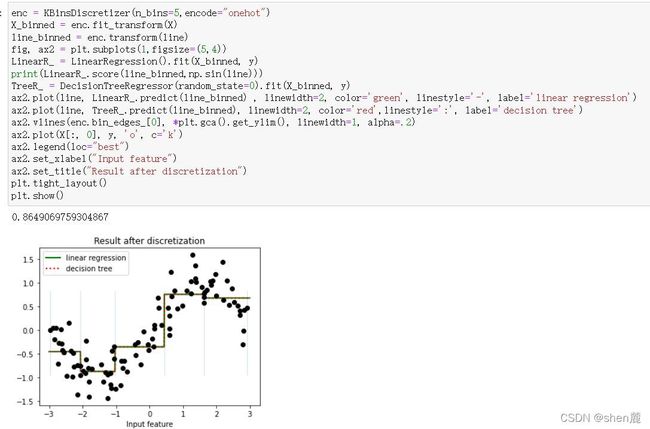
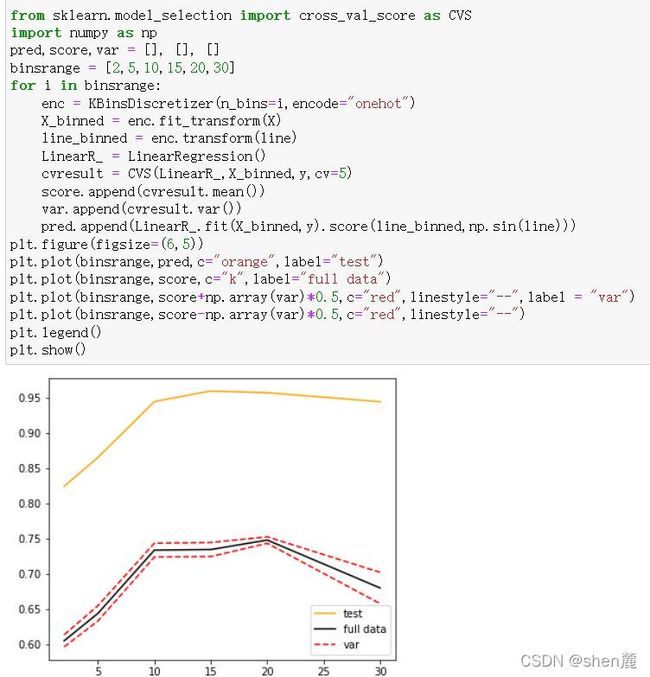
但是相反的,线性模型若用来拟合非线性数据或者对非线性可分的数据进行分类,那通常都会表现糟糕。通常如果我们已经发现数据属于非线性数据,或者数据非线性可分的数据,则我们不会选择使用线性模型来进行建模。改善线性模型在非线性数据上的效果的方法之一时进行分箱,并且从下图来看分箱的效果不是一般的好,甚至高过一些非线性模型。在下一节中我们会详细来讲解分箱的效果,但很容易注意到,在没有其他算法或者预处理帮忙的情况下,线性模型在非线性数据上的表现时很糟糕的。

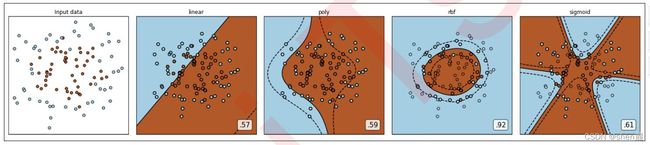
从上面的图中,我们可以观察出一个特性:线性模型们的决策边界都是一条条平行的直线,而非线性模型们的决策边界是交互的直线(格子),曲线,环形等等。对于分类模型来说,这是我们判断模型是线性还是非线性的重要评判因素:线性模型的决策边界是平行的直线,非线性模型的决策边界是曲线或者交叉的直线。之前我们提到,模型上如果自变量上的最高次方为1,则模型是线性的,但这种方式只适用于回归问题。分类模型中,我们很少讨论模型是否线性,因为我们很少使用线性模型来执行分类任务(逻辑回归是一个特例)。但从上面我们总结出的结果来看,我们可以认为对分类问题而言,如果一个分类模型的决策边界上自变量的最高次方为1,则我们称这个模型是线性模型。
既是线性,也是非线性的模型
对于有一些模型来说,他们既可以处理线性模型又可以处理非线性模型,比如说强大的支持向量机。支持向量机的前身是感知机模型,朴实的感知机模型是实打实的线性模型(其决策边界是直线),在线性可分数据上表现优秀,但在非线性可分的数据上基本属于无法使用状态。但支持向量机就不一样了。支持向量机本身也是处理线性可分数据的,但却可以通过对数据进行升维(将数据 转移到高维空间 中),将非线性可分数据变成高维空间中的线性可分数据,然后使用相应的“核函数”来求解。当我们选用线性核函数"linear"的时候,数据没有进行变换,支持向量机中就是线性模型,此时它的决策边界是直线。而当我们选用非线性核函数比如高斯径向基核函数的时候,数据进行了升维变化,此时支持向量机就是非线性模型,此时它的决策边界在二维空间中是曲线。所以这个模型可以在线性和非线性之间自由切换,一切取决于它的核函数。
还有更加特殊的,没有模型的算法,比如最近邻算法KNN,这些都是不建模,但是能够直接预测出标签或做出判断的算法。而这些算法,并没有线性非线性之分,单纯的是不建模的算法们。
讨论到这里,相信大家对于线性和非线性模型的概念就比较清楚了。来看看下面这张表的总结:
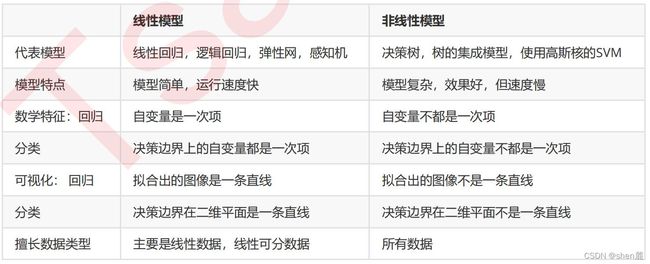
5.2 使用分箱处理非线性问题
让线性回归在非线性数据上表现提升的核心方法之一是对数据进行分箱,也就是离散化。与线性回归相比,我们常用的一种回归是决策树的回归。我们之前拟合过一条带有噪音的正弦曲线以展示多元线性回归与决策树的效用差异,我们来分析一下这张图,然后再使用采取措施帮助我们的线性回归。
5.3 多项式回归PolynomialFeatures
5.3.1 多项式对数据做了什么
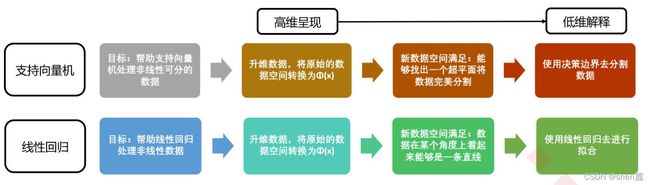
除了分箱之外,另一种更普遍的用于解决”线性回归只能处理线性数据“问题的手段,就是使用多项式回归对线性回归进行改进。这样的手法是机器学习研究者们从支持向量机中获得的:支持向量机通过升维可以将非线性可分数据转化为线性可分,然后使用核函数在低维空间中进行计算,这是一种“高维呈现,低维解释”的思维。那我们为什么不能让线性回归使用类似于升维的转换,将数据由非线性转换为线性,从而为线性回归赋予处理非线性数据的能力呢?当然可以
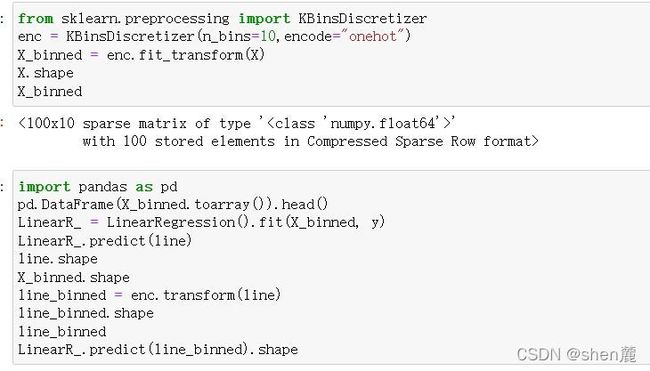
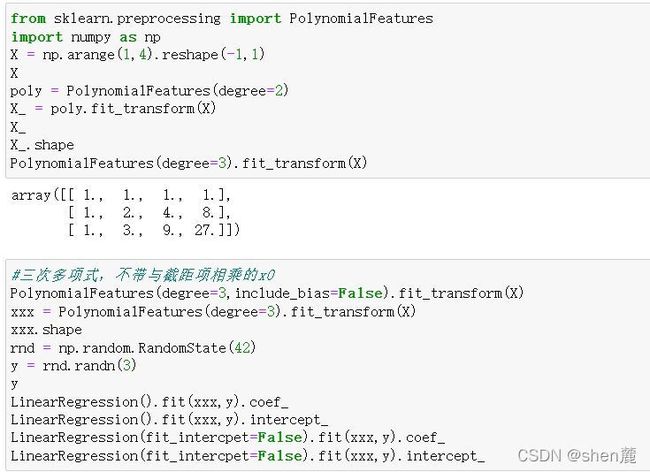
接下来,我们就来看看线性模型中的升维工具:多项式变化。这是一种通过增加自变量上的次数,而将数据映射到高维空间的方法,只要我们设定一个自变量上的次数(大于1),就可以相应地获得数据投影在高次方的空间中的结果。这种方法可以非常容易地通过sklearn中的类PolynomialFeatures来实现。我们先来简单看看这个类是如何使用
的。
class sklearn.preprocessing.PolynomialFeatures (degree=2, interaction_only=False, include_bias=True)

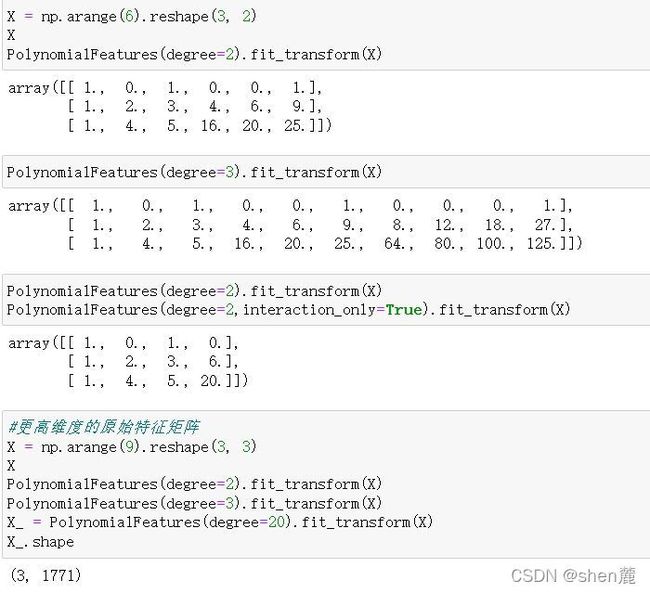
如此,多项式变化对于数据会有怎样的影响就一目了然了:随着原特征矩阵的维度上升,随着我们规定的最高次数的上升,数据会变得越来越复杂,维度越来越多,并且这种维度的增加并不能用太简单的数学公式表达出来。因此,多项式回归没有固定的模型表达式,多项式回归的模型最终长什么样子是由数据和最高次数决定的,因此我们无法断言说某个数学表达式"就是多项式回归的数学表达",因此要求解多项式回归不是一件容易的事儿,感兴趣的大家可以自己去尝试看看用最小二乘法求解多项式回归。接下来,我们就来看看多项式回归的根本作用:处理非线性问题。
5.3.2 多项式回归处理非线性问题
之前我们说过,是希望通过这种将数据投影到高维的方式来帮助我们解决非线性问题。那我们现在就来看一看多项式转化对模型造成了什么样的影响


5.3.3 多项式回归的可解释性
线性回归是一个具有高解释性的模型,它能够对每个特征拟合出参数 以帮助我们理解每个特征对于标签的作用。当我们进行了多项式转换后,尽管我们还是形成形如线性回归的方程,但随着数据维度和多项式次数的上升,方程也变得异常复杂,我们可能无法一眼看出增维后的特征是由之前的什么特征组成的(之前我们都是肉眼看肉眼判断)。不过,多项式回归的可解释性依然是存在的,我们可以使用接口get_feature_names来调用生成的新特征矩阵的各个特征上的名称,以便帮助我们解释模型。来看下面的例子:

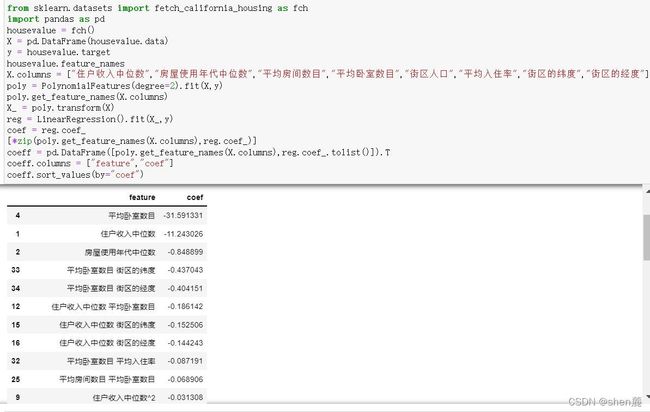

5.3.4 线性还是非线性模型?
狭义线性模型 vs 广义线性模型
狭义线性模型:自变量上不能有高此项,自变量与标签之间不能存在非线性关系。广义线性模型:只要标签与模型拟合出的参数之间的关系是线性的,模型就是线性的。这是说,只要生成的一系列 之间没有相乘或者相除的关系,我们就认为模型是线性的.
就多项式回归本身的性质来说,如果我们考虑狭义线性模型的定义,那它肯定是一种非线性模型没有错——否则如何能够处理非线性数据呢,并且在统计学中我们认为,特征之间若存在精确相关关系或高度相关关系,线性模型的估计就会被“扭曲“,从而失真或难以估计准确。多项式正是利用线性回归的这种”扭曲“,为线性模型赋予了处理非线性数据的能力。但如果我们考虑广义线性模型的定义,多项式回归就是一种线性模型,毕竟它的系数 之间也没有相乘或者相除。
另外,当Python在处理数据时,它并不知道这些特征是由多项式变化来的,它只注意到这些特征之间高度相关,然而既然你让我使用线性回归,那我就忠实执行命令,因此Python看待数据的方式是我们提到的第二种:并不了解数据之间的真实关系的建模。这也证明了多项式回归是广义线性模型。
所以,我们认为多项式回归是一种特殊的线性模型,不过要记得,它中间的特征包含了相当的共线性,如果处理线性数据,是会严重失误的.
总结一下,多项式回归通常被认为是非线性模型,但广义上它是一种特殊的线性模型,它能够帮助我们处理非线性数据,是线性回归的一种进化。大家要能够理解多项式回归的争议从哪里来,并且能够解释清楚观察多项式回归的不同角度,以避免混淆。