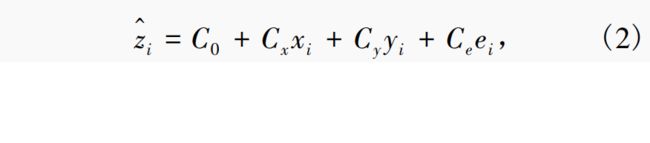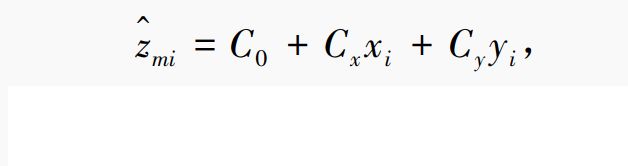python实现梯度距离平方反比法GIDS

1 梯度距离平方反比法

梯度距离平方反比法(gradient plus inverse distance squared (GIDS))由Nalder和Wein于1988年提出，是一种考虑了气象要素随经纬度和海拔高度变化的反距离权重法，其空间插值计算公式如下：

式中：

• $z$ 表示代插点的估算值
• $z_i$ 为第 $i$ 个样本点的实测值
• $d_i$ 为第 $i$ 个样本点与待插点之间的距离
• $n$ 为参与计算的实测样本点个数
• $x、y、e$ 分别为待插点的经度、纬度和海拔高度
• $x_i、y_i、e_i$ 分别为第 $i$ 个样本点的经度、纬度和海拔高度
• $C_x,C_y,C_e$ 分别为站点气象要素值与经度、纬度和海拔高度的偏回归系数，其值直接决定各样本点的插值权重，通过建立样本点的气象要素值与其经纬度和海拔高度的多元线性回归模型，利用最小二乘估计法对这3个系数进行求解，回归模型如下：

式中：

• $\widehat{z_i}$ 表示第 $i$ 个样本点的气象要素估计值
• $C_0$ 为回归常数

2 基于经验气温垂直递减率的梯度距离平方反比法

由上可知，样本点气象要素值与经纬度和海拔高度的关系直接决定空间插值的效果。

对气温进行空间插值时，当样本点海拔与待插值点之间的海拔相差较小时，可以得到准确度较高的插值结果; 但当研究区位于地形起伏剧烈区域时，待插值点与样本点的海拔高度差异较大，此时得到的偏回归系数 $C_x,C_y,C_e$ 不能准确描述待插值点气温与经纬和海拔高度的关系，所得插值误差就会较大，无法满足应用需求。

基于经验气温垂直递减率的改进梯度距离平方反比法 GIDS-EAR，考虑到海拔高度对气温的影响规律与经纬度不同，将海拔与经纬度的影响分开考虑：

• 首先根据气温垂直递减率经验值确定气温与海拔高度的偏回归系数$C_e$
• 并对样本点气温值 $z_i$ 进行修正得到 $z_{mi}$，消除由于海拔的差异对气温值的影响
• 再将 $z_{mi}$ 代入多元线性回归模型，作为模型最小二乘求解的样本点气温的初值，解算得到气温与经纬度的偏回归系数 $C_x,C_y$
• 再依据 GIDS 插值公式计算待插值点的温度值

GIDS-EAR 方法详细步骤如下:

1. $C_e$ 的确定: 考虑到海拔高度对气温的影响相较于经纬度更具有规律性，气温与海拔高度的偏回归系数与样本站点区域的气温垂直递减率接近，不同于 GIDS 法的线性回归求解，本文以气温垂直递减率的经验值 $T_g$ 作为各样本点气温值与海拔的偏回归系数 $C_e$，即 $C_e=T_g$;

2. $C_x、C_y$ 的求解: 由于第一步中已经考虑海拔高度对待插点气温的影响，故建立只考虑经纬度的多元线性回归模型，相应地，各样本点的气温值也应进行修正以消除海拔的影响， 如下：

式中: ${\hat{z}}_{mi}$ 为修正后第 $i$ 个样本点的气温估值。样本点气温修正值 $z_{mi}$ 的计算方法为：

3. 将上述所得 $C_x,C_y,C_e$ 代入式 (1) 中，求得基于经验气温垂直递减率的 GIDS 插值结果。

3 python实现

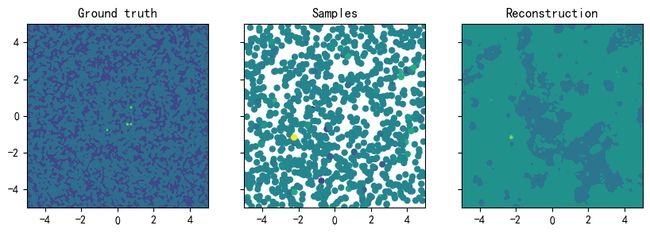
这是按自己理解复现的代码，感觉不是很对，效果不是很好，仅供参考。

from sklearn.cross_decomposition import PLSRegression

"""类函数"""
class GIDS:
    def __init__(self, x, y, elev, z, Tg=None):
        self.x, self.y, self.elev, self.z = x, y, elev, z
        self.Tg= Tg
        if Tg is None:
            feature = np.c_[x, y, elev]
        else:
            feature = np.c_[x, y]
        self.pls = PLSRegression(n_components=2)
        self.pls.fit(feature, z)

            
    def fit(self, x_new, y_new, elev_new):
        if self.Tg is None:
            feature_new = np.c_[self.x-x_new, self.y-y_new, self.elev-elev_new]
            z_new = self.pls.predict(feature_new)
        else:
            feature_new = np.c_[self.x-x_new, self.y-y_new]
            z_new = self.pls.predict(feature_new)+self.Tg*(self.elev-elev_new)

        di = (self.x-x_new)**2+(self.y-y_new)**2
        z = np.sum((self.z+z_new)/di)/np.sum(1/di)
        return z 


"""demo"""
import numpy as np
import matplotlib.pyplot as plt

# create sample points with structured scores
X1 = 10 * np.random.rand(1000, 2) -5
elev = np.random.randint(1, 100, 1000)

def func(x, y, z):
    return np.sin(x**2 + y**2+ z**2) / (x**2 + y**2 + z**2)

z1 = func(X1[:,0], X1[:,1], elev)

# 'train'
gids = GIDS(X1[:,0], X1[:,1], elev, z1)


# 'test'
spacing = np.linspace(-5., 5., 100)
X2 = np.meshgrid(spacing, spacing)
grid_shape = X2[0].shape
X2 = np.reshape(X2, (2, -1)).T
elev2 = np.random.randint(1, 100, X2.size//2)
z2 = []
for x2,y2, elev in zip(X2[:,0],X2[:,1], elev2):
    z2.append(gids.fit(x2, y2, elev))
z2 = np.array(z2)

# plot
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharex=True, sharey=True, figsize=(10,3))
ax1.contourf(spacing, spacing, func(*np.meshgrid(spacing, spacing), elev2.reshape(100,100)))
ax1.set_title('Ground truth')
ax2.scatter(X1[:,0], X1[:,1], c=z1, linewidths=0)
ax2.set_title('Samples')
ax3.contourf(spacing, spacing, z2.reshape(grid_shape))
ax3.set_title('Reconstruction')
plt.show()

参考：一种适用于气温空间插值的改进梯度距离平方反比法*.李框宇等.