MySQL中的索引
目录
一、概念
二、作用和特点
作用
特点
三、使用场景
四、使用
1、查看索引
2、创建索引
3、删除索引
五、索引底层数据结构的实现
B树(B-树)
B+树
特点
重复出现的好处
一、概念
索引 翻译成英文:index(下标)
现有如下场景,有一张表是存放书的,我们如何查找其中的一本书?在数据库中,进行条件查找时,是要遍历数据的,时间复杂度虽然是O(N) , 但是数据库里的表里的数据是成千上万的,就要遍历很多次,查找的速度也就变慢了,那么我们如何能快速找到这表里我们想要的书呢?这时,就可以在数据库中引入索引,通过这个索引来快速找到我们想要的数据。
概念:索引是一种特殊的文件,包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引,并指定索引的类型,各类索引有各自的数据结构实现。
二、作用和特点
作用
1、数据库中的表、数据、索引之间的关系,类似于书架上的图书、书籍内容和书籍目录的关系。
2、索引所起的作用类似书籍目录,可用于快速定位、检索数据。
3、索引对于提高数据库的性能有很大的帮助
特点
1、加快查询的速度。
2、索引自身是一定的数据结构,也要占据存储空间。
3、当我们进行新增、修改、删除的时候,也要针对其索引进行更新,会有额外的开销。
三、使用场景
1、对于存储空间要求不高(存储空间比较充裕)
2、应用场景中,查询的比较多,增加、修改和删除都不多。
四、使用
在MySQL中创建主键(primary key)、唯一约束(unique)、外键约束(foreign key)时,会自动创建对应的索引。’
1、查看索引
语法:show index from 表名;
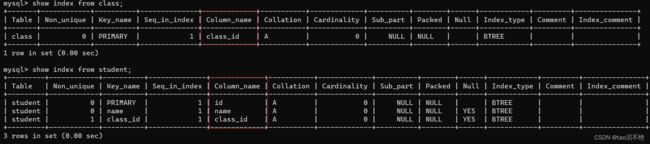
先创建有两个表,如图:
查看这两表的索引
代码:
show index from class; show index from student;如图:
2、创建索引
语法:create index 索引名 on 表名(字段名);
例子:对student表里的name创建索引
代码:
create index index_student_name on student(name);3、删除索引
语法:drop index 索引名 on 表名;
例子:删除student中name的索引
代码:
drop index index_student_name on student;五、索引底层数据结构的实现
索引是通过额外的数据结构,来针对表里的数据进行重新组织
我们知道,在MySQL中查找的时候有时不只是单单找一个值,可以是有范围的数据,如加入比较运算符:"<",">","between ... and..",这时用hash表或者是二叉搜索树来查找就不是很合适了,因为他们找的都是一个具体的值,而不是范围。
那么通过索引进行查找,数据要怎么存储,查找的速度才能比较快呢?
——针对索引,MySQL专门搞了一个数据结构,来存储索引的列的数据,名为B+树
我们想要了解B+树要先了解B树
B树(B-树)
概念:B树是一个N叉搜索树(要求是有序的),其实就是对二叉搜索树进行了扩展
一个节点有N个值,N个值这又划分了N + 1个区间,到下一个节点又是重复上一节点的步骤进行划分区间。
图展示:
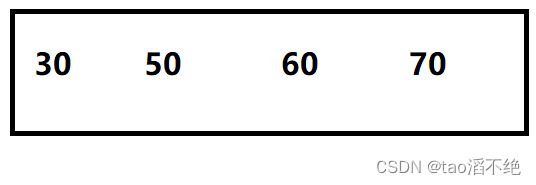
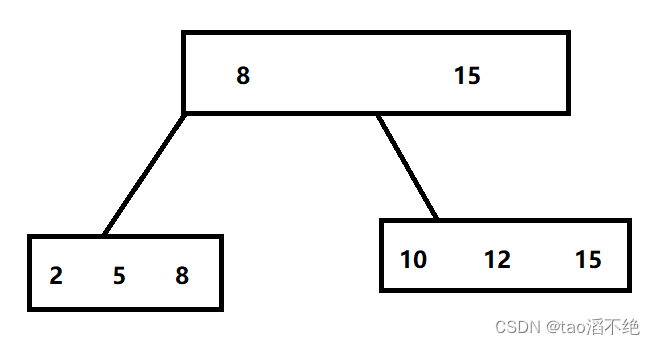
如图:假设第一个节点有以下这些值,我们存放有以下值
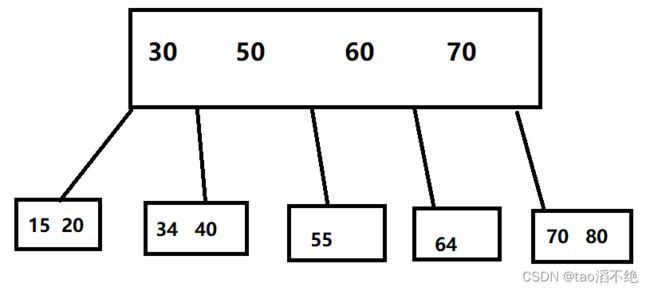
那么我们可以划分为5个区间,小于30, 30~50,50~60,60~70,大于70,这五个区间下就可以放属于这五个区间的数据,如图:
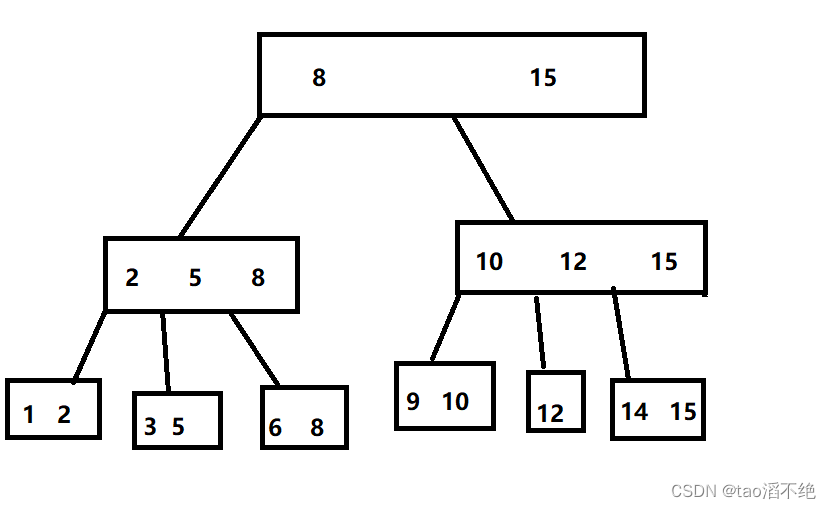
第二层节点下面还能划分,具体有啥值就不写了,如图:
这样,我们可以查找某一个具体的值,也可以找一个范围。而且在同样高度的树,能表示的元素也比二插搜索树多了很多;使用B树来查询的时候,比较次数要比二插搜索树要更多;但是这里的关键在于,同一个节点的这些key值,都是一次硬盘IO就读出来了。
即使总的比较次数增加了,但是硬盘IO的次数减少了,这里的一次硬盘IO相当于在内存中1w次比较
B+树
B+树是在B树对基础上,做出了改进
同样是N插搜索树,每个节点包含了多个key,N个key划分出N个区间,如图:
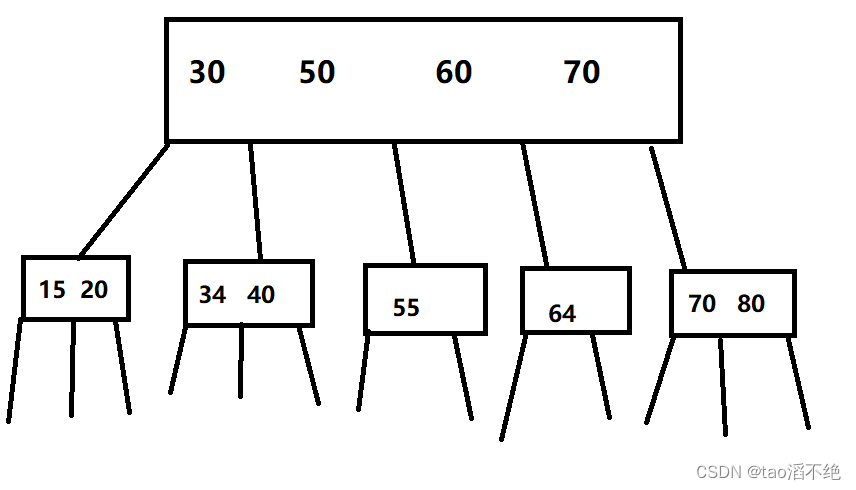
再往下
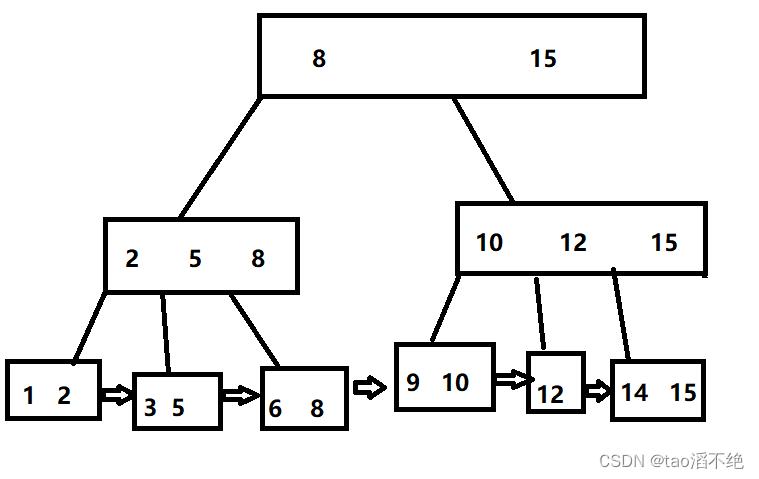
这时又有一个和B树不一样的操作,就是会把叶子节点连接起来,如图:
这样,我们每次查询一个数或者一个范围,都需要从根节点到叶子节点,再从叶子节点的去往后遍历连接起来的叶子节点,去找我们需要的值或者区间。
特点
1、N叉搜索树,每个节点包含N个key,N个key可以划分出N个区间。
2、每个节点的的N个key中,都会存在一个最大值(设定成最小值也一样)。
3、每个节点中的key(最大值),都会在子树中重复出现。
4、叶子节点用链式结构连接起来
重复出现的好处
1、所有数据都包含在叶子节点这一层中(数据全集)。如找id > 4 and id < 10,根据4找到相应的位置,再从这个位置往后找到10就可以了;如果没有这种链式结构,就可能要反复对树进行回溯查找,这样就很麻烦。
2、针对B+树的的查询的时间是稳定的。查询任何一个元素,都要从根节点查询到子节点,过程中经过的硬盘IO次数是一样的。
3、数据行只需在叶子节点中存储,其他非叶子节点只存储key即可。
比如学生表(id,name,score...)数据行,这些数据行存储到叶子节点即可,因此,非叶子节点只存储key,按照一个key有4个字节来计算,100w个key才4MB,而这些非叶子节点的数据可以缓存到内存中,这个时候就可以在查询的时候,只在内存中,比较了,大幅度减少硬盘IO的次数。