编译原理个人作业--第三章

第三章

7

构造下列正规式相应的DFA

(1)	1(0|1)*101
(2)	1(1010*|1(010)*1)*0
(3)	0*10*10*10*
(4)	(00|11)*((01|10)(00|11)*(01|10)(00|11)*)*

复习概念：

1. DFA没有输入空串之上的转换动作；
2. 对于DFA，一个特定的符号输入，有且只能得到一个状态，而NFA就有可能得到一个状态集；

(1)

先将NFA画出

NFA转换为DFA

能发生转换的数据为$1,0,ϵ$,初态为$0$,且它的$ϵ$闭包为$\{0\}$, 所以不妨先求出$I=0的I_0与I_1$

$I_0$表示，从$I$的元素出发，只经过一次$0$状态转化可以到达的元素集合

$I_1$表示，从$I$的元素出发，只经过一次$1$状态转化可以到达的元素集合

$I$	$I_0$	$I_1$
$\{0\}$	$\varnothing$	$\{1,2,3\}$

这里产生了新的非空集合$\{1,2,3\}$,需要对该集合作为新的$I$进行处理

$I$	$I_0$	$I_1$
$\{1,2,3\}$	$\{2,3\}$	$\{2,3,4\}$
注意，$ϵ$变化直接默认放进去

于是产生了新的集合$\{2,3\}$和$\{2,3,4\}$，继续对新集合产生上述操作

最后得到全部 状态转换矩阵

$I$	$I_0$	$I_1$	说明
$\{0\}$	$\varnothing$	$\{1,2,3\}$	新集合$\{1,2,3\}$
$\{1,2,3\}$	$\{2,3\}$	$\{2,3,4\}$	新集合$\{2,3\}$，$\{2,3,4\}$,1没有0的状态转移，删去
$\{2,3\}$	$\{2,3\}$	$\{2,3,4\}$	无新集合
$\{2,3,4\}$	$\{2,3,5\}$	$\{2,3,4\}$	新集合$\{2,3,5\}$
$\{2,3,5\}$	$\{2,3\}$	$\{2,3,4,6\}$	新集合$\{2,3,4,6\}$,注意5没有0的状态转移，删去
$\{2,3,4,6\}$	$\{2,3,5\}$	$\{2,3,4\}$	无新集合
$\varnothing$	$\varnothing$	$\varnothing$	无新集合

重命名

$I$	$I_0$	$I_1$
0	$\varnothing$	1
1	2	3
2	2	3
3	4	3
4	2	5
5	4	3
$\varnothing$	$\varnothing$	$\varnothing$

然后我们还需要最小化状态转换矩阵，我们对所有的状态有如下定义

1. 多余状态：对于一个状态$S_i$，若从开始状态出发，不可能到达状态$S_i$，则$S_i$为多余（无用）状态
2. 死状态：对于一个状态$S_i$，对于任意输入符号a，若转到它本身后，不可能从它到达终止状态，则称$S_i$为死状态
3. 等价状态：若$S_i$为自动机的一个状态，我们把从$S_i$出发能导出的所有符号串的集合记为$L(S_i)$.
   若有$L(S_i)=L(S_{i}j)$.则称$S_i$和$S_j$是等价状态。
4. 可区别状态：自动机中两个状态$S_i$和$S_j$，如果它们不等价，则称它们可区别
   如何判断？
   • 状态$S_i$和$S_j$必须同时为终止状态或同时为非终止状态
   • 状态$S_i$和$S_j$对于任意输入符$a\in \Sigma$，必须转到等价的状态里

综上我们要去掉前两种状态，并合并等价状态

首先删去空集状态，其为死状态。

然后能到达原NFA中6状态的都是终态，也就是说重命名后的状态5为终态,记$\{5\}$为$I^{(2)}$;剩余状态0,1,2,3,4为非终态， 记$\{0,1,2,3,4\}$为$I^{(1)}$；

不难发现$\{5\}$无法划分,

$$I_0^{(1)}=\{2,4\}{I}_1^{(1)}=\{1,3,5\}$$
其中$\{1,3,5\}$不包含于任何划分，需要拆分$I^{(1)}$

注意到只有4经过1到达5,需要将4划分出来

变成

$$\begin{gathered} \{0,1,2,3\}记为I^{(11)} \\ \{4\}记为I^{(12)} \end{gathered}$$

显然$I^{(12)}$无法划分，继续考察$I^{(11)}$

$$I_0^{(11)}=\{2,4\}{I}_1^{(11)}=\{1,3\}$$

$\{2,4\}$不包含于任何划分

注意到只有3经过0到达4,需要将3划分出来

$$\begin{gathered} \{0,1,2\}记为I^{(tmp)} \\ \{3\}记为I^{(112)} \end{gathered}$$

$$I_0^{(tmp)}=\{2\}{I}_1^{(tmp)}=\{1,3\}$$

划分之后发现$\{1,3\}$也不被包含于新的划分了，需要继续划分$I^{(tmp)}$:0通过1转化为1，所以将0划分
$$\begin{gathered} \{1,2\}记为I^{(111)} \\ \{0\}记为I^{(113)} \end{gathered}$$

最后得到划分
$$\{0\}\{1,2\}\{3\}\{4\}\{5\}$$
并重命名为 0，1，2，3，4

得到最简状态矩阵转换表

$I$	$I_0$	$I_1$
0		1
1	1	2
2	3	2
3	1	4
4	3	2

最简DFA如下

(2)

对于 1(1010*|1(010)*1)*0
被()*包围住的部分可以使用循环来表示

然后进入循环的部分两旁使用$ϵ$进行循环的离开
如 1010* 和 1(010)*1可以表示为如下NFA

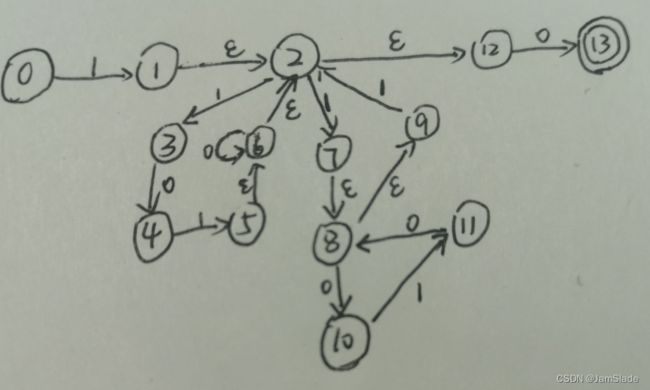
整体的NFA如下

初始状态转换矩阵

$I$	$I_0$	$I_1$
$\{0\}$	$\varnothing$	$\{1,2,12\}$
$\{1,2,12\}$	$\{13\}$	$\{3,7,8,9\}$
$\{13\}$	$\varnothing$	$\varnothing$
$\{3,7,8,9\}$	$\{4,10\}$	$\{2,12\}$
$\{4,10\}$	$\varnothing$	$\{5,6,2,12,11\}$
$\{2,12\}$	$\{13\}$	$\{3,7,8,9\}$
$\{2,5,6,12,11\}$	$\{2,6,8,9,12,13\}$	$\{3,7,8,9\}$
$\{2,6,8,9,12,13\}$	$\{2,6,10,12,13\}$	$\{2,3,7,8,9,12\}$
$\{2,6,10,12,13\}$	$\{2,6,12,13\}$	$\{3,7,8,9,11\}$
$\{2,6,12,13\}$	$\{2,6,12,13\}$	$\{3,7,8,9\}$
$\{2,3,7,8,9,12\}$	$\{4,10,13\}$	$\{2,3,7,8,9,12\}$
$\{3,7,8,9,11\}$	$\{4,8,9,10\}$	$\{2,12\}$
$\{4,10,13\}$	$\varnothing$	$\{2,5,6,11,12\}$
$\{4,8,9,10\}$	$\{10\}$	$\{2,5,6,11,12\}$
$\{10\}$	$\varnothing$	$\{11\}$
$\{11\}$	$\{8,9\}$	$\varnothing$
$\{8,9\}$	$\{10\}$	$\{2,12\}$

重命名

$I$	$I_0$	$I_1$
0	∅	1
1	2	3
3	4	5
4	∅	6
5	2	3
6	7	3
7	8	10
8	9	11
9	9	3
10	12	10
11	13	5
12	∅	6
13	14	6
14	∅	15
15	16	∅
16	14	5

终态集合$\{2,7,8,9,12\}$,
非终态集合$\{1,3,4,5,6,10,11\}$

拆分后有
$$\{1,5\},\{0\},\{2\},\{3\},\{4\},\{6\},\{7\},\{8\},\{9\},\{10\},\{11\},\{12\},\{13\},\{14\},\{15\},\{16\}$$

1和5合并为1后，状态图如下

(3)

0*10*10*10*的NFA如下图

初态$I$集合为$\{0,1,2\}$

$I$	$I_0$	$I_1$
$\{0,1,2\}$	$\{1,2\}$	$\{3,4,5\}$
$\{1,2\}$	$\{1,2\}$	$\{3,4,5\}$
$\{3,4,5\}$	$\{4,5\}$	$\{6,7,8\}$
$\{4,5\}$	$\{4,5\}$	$\{6,7,8\}$
$\{6,7,8\}$	$\{7,8\}$	$\{9,10,11\}$
$\{7,8\}$	$\{7,8\}$	$\{9,10,11\}$
$\{9,10,11\}$	$\{10,11\}$	$\varnothing$
$\{10,11\}$	$\{10,11\}$	$\varnothing$

重命名

$I$	$I_0$	$I_1$
0	1	2
1	1	2
2	3	4
3	3	4
4	5	6
5	5	6
6	7	∅
7	7	∅

得到未化简DFA

非终态$\{0,1,2,3,4,5\}$;终态$\{6,7\}$

显然$\{6,7\}$无须划分

$I^{(1)}$	$I_0^{(1)}$	$I_1^{(1)}$
$\{0,1,2,3,4,5\}$	$\{1,3,5\}$	$\{2,4,6\}$

$\{2,4,6\}$不包含于任何划分，需要将能转换为6的状态$4，5$划分

$$I^{(11)}=\{0,1,2,3\}{I}^{(12)}=\{4,5\}$$

同理继续划分

$I^{(11)}$	$I_0^{(11)}$	$I_1^{(11)}$
$\{0,1,2,3\}$	$\{1,3\}$	$\{2,4\}$
将3与2划分出$I^{(11)}$
$$I^{(111)}=\{0,1\}{I}^{(112)}=\{2,3\}$$

最后的划分
$$\{0,1\}\{2,3\}\{4,5\}\{6,7\}$$
经检验，他们经0、1转换后的集合都包含于现有划分

$I$	$I_0$	$I_1$
$\{0,1\}$	$\{1\}\subseteq \{0,1\}$	$\{2\}\subseteq \{2,3\}$
$\{2,3\}$	$\{3\}\subseteq \{2,3\}$	$\{4\}\subseteq \{4,5\}$
$\{4,5\}$	$\{5\}\subseteq \{4,5\}$	$\{6\}\subseteq \{6,7\}$
$\{6,7\}$	$\{6\}\subseteq \{6,7\}$

更名得到最简DFA

(4)

NFA如下

$I$	$I_0$	$I_1$
$\{0,1,4,5,19\}$	$\{2,6\}$	$\{3,8\}$
$\{2,6\}$	$\{1,4,5,19\}$	$\{7,9,12\}$
$\{3,8\}$	$\{7,9,12\}$	$\{1,4,5,19\}$
$\{1,4,5,19\}$	$\{2,6\}$	$\{3,8\}$
$\{7,9,12\}$	$\{10,13\}$	$\{11,15\}$
$\{10,13\}$	$\{9,12\}$	$\{5,14,16,19\}$
$\{11,15\}$	$\{5,14,16,19\}$	$\{9,12\}$
$\{9,12\}$	$\{10,13\}$	$\{11,15\}$
$\{5,14,16,19\}$	$\{6,17\}$	$\{8,18\}$
$\{6,17\}$	$\{5,16,19\}$	$\{7,9,12\}$
$\{8,18\}$	$\{7,9,12\}$	$\{5,16,19\}$
$\{5,16,19\}$	$\{6,17\}$	$\{8,18\}$

重命名

$I$	$I_0$	$I_1$
0	1	2
1	3	4
2	4	3
3	1	2
4	5	6
5	7	8
6	8	7
7	5	6
8	9	10
9	11	4
10	4	11
11	9	10

非终态$\{1,2,4,5,6,7,9,10\}$;终态$\{0,3,8,11\}$

划分过程略,最终化简
$$\{3,6,8,11\}\{1,6,9\}\{4,7\}\{2,5,10\}$$

8

(1) 01结尾的二进制数串

$$(0|1{)}^{\ast }01$$

(2) 被5整除的10进制整数

$$((+|-)(((1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9{)}^{\ast }(0|5))|5))|0$$

解释

1. 不被括号括住的分隔符的左边是((+|-)(((1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)^*(0|5))|5)),内部可分为两部分
   1. 第一部分 (+|-)表示+整数，-负数
   2. 第二部分(((1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)^*(0|5))|5),可以根据分隔符继续分成两部分
      1. 左边部分((1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)^*(0|5))表示至少为2位的能被5整除的正整数
      2. 5指单独的数字5
2. 还有不被括号括住的分隔符的右边表示0

(3) 奇数个1或奇数个0的二进制数串

$$0^{\ast }1(0|10^{\ast }1{)}^{\ast }|1^{\ast }0(1|01^{\ast }0)$$

12 确定化、最小化下图的(a)(b)

(a)

$I$	$I_a$	$I_b$
$\{0\}$	$\{0,1\}$	$\{1\}$
$\{0,1\}$	$\{0,1\}$	$\{1\}$
$\{1\}$	$\{0\}$	$\varnothing$

重命名后为：

$I$	$I_a$	$I_b$
0	1	2
1	1	2
2	1	$\varnothing$

非终态$\{2\}$;终态$\{0,1\}$
$\{0,1{\}}_a=\{1\}\subseteq \{0,1\}$
$\{0,1{\}}_b=\{2\}\subseteq \{2\}$

已经是最优划分

最简DFA为

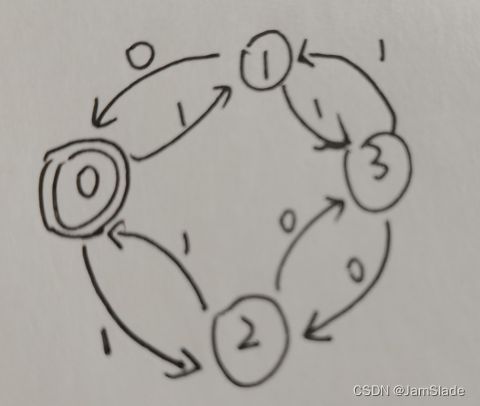
(b)

本题已经确定化了，需要进行最小化
考虑到划分

$$I^{(1)}=\{0,1\}与I^{(2)}=\{2,3,4,5\}$$

$I_a^{(2)}=\{0,1,3,5\}$
需要划分为
$$I^{(21)}=\{2,3\}{I}^{(22)}=\{4,5\}$$

最终将$ {0,1}\quad {2,3}\quad {4,5}$重命名

14

构造DFS，令其满足

$$\sum =\{0,1\}\wedge “每个1都有0直接跟在右边”的字符串$$

正规式(0|10)^*

NFA

$I$	$I_0$	$I_1$
$\{X,0,Y\}$	$\{0,Y\}$	$\{1\}$
$\{0,Y\}$	$\{0,Y\}$	$\{1\}$
$\{1\}$	$\{0,Y\}$	$\varnothing$

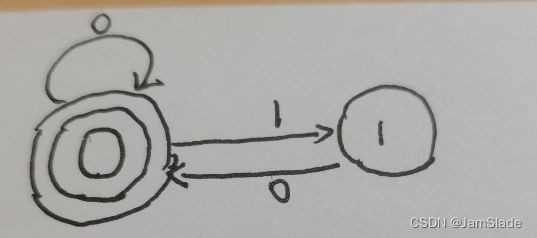
重命名的DFA如下

观察划分
$$\{0,1\}与\{2\}$$
显然0，1可以进行合并，得到最简DFA