九宫格拼图，避免不可还原

判断拼图可还原性

对于九宫格拼图，如果随机打乱的话，有50%的概率会出现不可还原的情况。
可以采用求逆序数的方法避免不可还原的情况。

逆序数：即在一个数列中，每两个数构成一个数对，如果数对中左边的数小于右边的数，则此数对是顺序对，如果左边的数大于右边的数，则此数对就是一个逆序对，数列的所有数对中逆序对的总数就是该数列的逆序数。
例： 0, 3, 1, 2 这个数列中，(0,3),(0,1),(0,2)都是顺序对，(3,1)是逆序对，(3,2)是逆序对，(1,2)是顺序对，只有两个数对是逆序对，所以这个数列的逆序数是2。

三阶拼图

在求解拼图的可还原性时需要把空白块去掉，因为空白块是可以自由移动的，计算它的逆序会增加复杂性。
对于 3 x 3 的拼图，把每一个图块标号为 0,1,2,3,4,5,6,7,8，去掉空白块8号后，保证非空白的8块（即标号为0,1,2,3,4,5,6,7的图块）组成序列的逆序数为偶数即可保证拼图可还原。

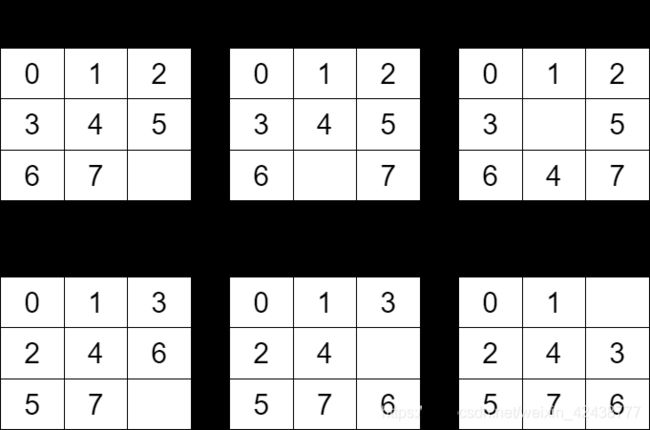
如上图所示，图①到图②交换了空白块与图块7，逆序数没有变，都为0，图②到图③交换了空白块与图块4，逆序数增加到2，图④的逆序数为2，交换空白块与图块6后变成图⑤的情况，逆序数还是2，再将图块3与空白块交换变成图⑥的情况，逆序数还是2。
从中可以看出，在水平方向交换空白块与其他图块时，整个数列（去掉空白块后）所有数字的顺序是完全不变的，只有在垂直方向上交换空白块与其他块时，某些数字的顺序才会改变，并且只改变了三个数的顺序，如图②到图③，由4,5,6改变为5,6,4，也就是将4往后移动了2个位置，其他数字与这三个数字的相对顺序都是没有改变的，所以数列逆序数的改变取决于这三个数内部的逆序数的变化，而这三个数的逆序数的改变取决于移动的数与另外两个数的大小关系，在这里移动的是4，另外两个数是5与6，都大于4，所以移动4，逆序数将会加2或减2，而图⑤到图⑥，由3,2,4改变成2,4,3，将3往后移动了2个位置，移动的是3，另外两个数是2与4，一个大于3一个小于3，所以移动3之后，逆序数不变，因此我们可以得出结论：每次交换空白块与其他图块时，无论是水平方向还是垂直方向，数列逆序数要么加减2，要么不变，所以三阶拼图的图块标号构成的数列，其逆序数为偶数，这个拼图就是可以还原的。

四阶拼图

接下来分析 4 x 4 的拼图，用 0,1,2,…14,15 来标记每一块图块，15为空白块，此处将它去掉。

与 3 x 3 拼图有点不同，4 x 4 的拼图在垂直方向交换空白块与其他图块时，将影响到4个数的顺序变化，也即逆序数将会受到移动的数字与另外三个数的大小关系的影响，三个数都大于或小于移动的数字，那么逆序数会加3或者减3，两个数大而一个数小，或者两个数小而一个数大，那么逆序数会加1或者减1，总之在移动一次时，其逆序数不会改变2，而我们可以确定在还原好的情况下，其逆序数是0，又由于水平方向移动不会影响逆序数，因此我们可以得出结论：其可还原性与空白块所在行有相关性，即对于四阶拼图，空白块在4、2行（行索引为3、1）时，逆序数为偶数才能保证拼图可还原，空白块在3、1行（行索引为2、0）时，逆序数为奇数才能保证拼图可还原。

五阶拼图

5 x 5 拼图与 3 x 3 拼图分析过程类似，在垂直方向上交换空白块与其他块时，影响到5个数的顺序变化，也即逆序数将会受到移动的数与另外四个数的大小关系影响，可能的变化为0、2、4，因此五阶拼图，逆序数由偶数即可保证拼图的可还原性。

逆序数计算

计算逆序数的方法可以参考基本排序算法。
以下采用归并排序的思想计算逆序数，时间复杂度为O(NlogN)。

// 判断拼图是否可还原
BOOL CPuzzleDlg::IsReducible(vector<UINT>& vecIndex)
{
    // 最后一个标号是可以移动的，故计算逆序数时应去掉，3阶时去掉标号8，4阶时去掉标号15，5阶时去掉24
    vector<UINT> vecIndexCopy = vecIndex;
    auto itLastIdx = find(vecIndexCopy.begin(), vecIndexCopy.end(), m_nLastCtlIdx);
    ASSERT(itLastIdx != vecIndexCopy.end());
    int nLastIndex = itLastIdx - vecIndexCopy.begin();
    vecIndexCopy.erase(itLastIdx);

    // 逆序是高等数学里面的概念，即在数列当中某两个数字（每两个数构成一个数对）是前面的数
    // 大于后面的数，则这个数对的一个逆序对，逆序数即为该数列中逆序对的总数，
    // 例：0 2 1 3 4 7 5 6，该数列中共有8个数，有7+6+5+4+3+2+1=28个数对，
    // 其中 (2,1),(7,5),(7,6) 是逆序对，(0,2),(2,3),(1,6)等等都是顺序对，
    // 所以本数列的逆序数是3
    // 此处用归并排序的方式计算逆序数
    int nInversePairs = InversePairsCore(vecIndexCopy.data(), 0, vecIndexCopy.size() - 1);

    // 如果是3或5阶，逆序数为偶数才能被还原，
    // 如果是4阶，则需判断空白块所在行数，行索引为0、2时逆序数要为奇数，行索引为1、3时，行索引要为偶数
    if (m_nLine == 3 || m_nLine == 5) {
        return (nInversePairs & 1) == 0;
    } else if (m_nLine == 4) {
        return ((nLastIndex / m_nLine) & 1) != (nInversePairs & 1);
    } else {
        return FALSE;
    }
}

// 计算逆序数
int CPuzzleDlg::InversePairsCore(UINT* pData, int nLeft, int nRight)
{
    if (nRight - nLeft <= 0) {
        return 0;
    }
    int nMid = nLeft + ((nRight - nLeft) >> 1);
    int nLeftPairs = InversePairsCore(pData, nLeft, nMid);
    int nRightPairs = InversePairsCore(pData, nMid + 1, nRight);
    int nMergeCount = InversePairsMerge(pData, nLeft, nRight);
    return nLeftPairs + nRightPairs + nMergeCount;
}

// 归并排序方法计算逆序数
int CPuzzleDlg::InversePairsMerge(UINT* pData, int nLeft, int nRight)
{
    int nMid = nLeft + ((nRight - nLeft) >> 1);
    int* pTemp = new int[nRight - nLeft + 1];
    int nLeftIdx = nLeft, nRightIdx = nMid + 1, nIndex = 0;
    int nInversePairs = 0;
    while (nLeftIdx <= nMid && nRightIdx <= nRight) {
        if (pData[nLeftIdx] < pData[nRightIdx]) {
            pTemp[nIndex++] = pData[nLeftIdx++];
        } else {
            pTemp[nIndex++] = pData[nRightIdx++];
            nInversePairs += nMid - nLeftIdx + 1;
        }
    }
    while (nLeftIdx <= nMid) {
        pTemp[nIndex++] = pData[nLeftIdx++];
    }
    while (nRightIdx <= nRight) {
        pTemp[nIndex++] = pData[nRightIdx++];
    }
    memcpy(pData + nLeft, pTemp, sizeof(int) * (nRight - nLeft + 1));
    delete[] pTemp;
    return nInversePairs;
};

此处感谢评论区朋友的点评，此文章是在评论区朋友的提示后修改完成的。

源码链接：九宫格拼图源码-Gitee
源码链接：九宫格拼图源码-CSDN资源