Learning Convolutional Neural Networks for Graphs
The paper proposed a framework for learning graph representations that are especially beneficial in conjunction with CNNs. It combines two complementary procedures:
(a) selecting a sequence of nodes that covers large parts of the graph
(b) generating local normalized neighborhood representations for each of the nodes in the sequence

Graph kernels
Kernels on graphs were originally defined as similarity functions on the nodes of a single graph.
Two representative classes of kernels are the skew spectrum kernel and kernels based on graphlets.
The latter builds kernels based on fixed-sized subgraphs.These subgraphs, which are often called motifs or graphlets, reflect functional network properties.
Due to the combinatorial complexity of subgraph enumeration, graphlet kernels are restricted to subgraphs with few nodes.
Weisfeiler-Lehman (WL) kernels: only support discrete features and use memory linear in the number of training examples at test time.
Deep graph kernels and graph invariant kernels: compare graphs based on the existence or count of small substructures such as shortest paths, graphlets, subtrees, and other graph invariants.
Graph neural networks (GNNs)
A recurrent neural network architecture defined on graphs.
GNNs support only discrete labels and perform as many backpropagation operations as there are edges and nodes in the graph per learning iteration.
Gated Graph Sequence Neural Networks modify GNNs to use gated recurrent units and to output sequences .
A brief introduction to graph theory
A graph G is a pair (V, E) with V = {v1, …, vn} the set of vertices and E ⊆ V × V the set of edges.
d(u, v):the distance between u and v, that is, the length of the shortest path between u and v.
N1(v) is the 1-neighborhood of a node, that is, all nodes that are adjacent to v.
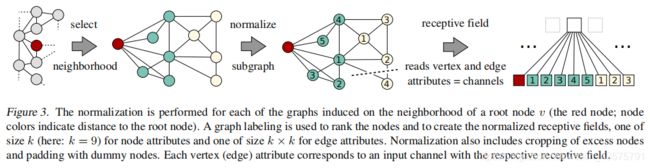
PATCHY-SAN:
learns substructures from graph data and is not limited to a predefined set of motifs. Moreover, while all graph kernels have a training complexity at least quadratic in the number of graphs, which is prohibitive for large-scale problems,PATCHY-SAN scales linearly with the number of graphs.
Given a collection of graphs, PATCHY-SAN (SELECT- SSEMBLE-NORMALIZE) applies the following steps to each graph:
(1) Select a fixed-length sequence of nodes from the graph;
(2) assemble a fixed-size neighborhood for each node in the selected sequence;
(3) normalize the extracted neighborhood graph;
(4) learn neighborhood representations with convolutional neural networks from the resulting sequence of patches.
1)Node Sequence Selection

If the number of nodes is smaller than w, the algorithm creates all-zero receptive fields for padding purposes.
2) Neighborhood Assembly

the size of N is possibly different to k.
The receptive field for a node is constructed by normalizing the neighborhood assembled in the previous step.
The basic idea is to leverage graph labeling procedures that assigns nodes of two different graphs to a similar relative position in the respective adjacency matrices if and only if their structural roles within the graphs are similar.
Something Else
the restricted Boltzman machine (RBM)
1-dimensional Weisfeiler-Lehman (1-WL)
distance measure on graphs
distance measure on k × k matrices