LPA*算法图文详解

之前我们看过了A* 算法，知道了A* 算法的基本原理，但是A* 算法的缺陷也很明显：它是离线的路径规划算法，只能一次规划出路径，但是后面路径被改变的话就无法生效了。针对这个问题，人们研究出了D* 算法。D* 算法相对于A* 也好还是Dijkstra算法也好它最大的优点就是再于它在运动过程中是实时的：在原先规划的路径上如果出现障碍物的话，会对当前路径进行新的规划，通过较短的迭代即可找到新的路径。但是它比较大的问题在于它只能处理空白路径上出现障碍物的情况，而不能处理本来是障碍物但是变成空白区域的情况。而针对这种情况，LPA* 算法诞生啦！

LPA* 算法基本原理：

LPA* 保持每个单元的起始距离的两个估计，即g值和rhs值。g值直接对应于A*搜索的g值。rhs值是基于g值的一步前瞻值。rhs值是始终满足以下关系（基于g值）：

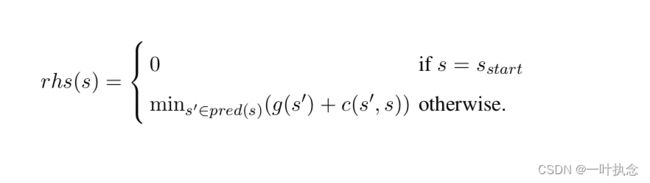
起始单元格的rhs值为零。任何其他位置的rhs值是邻居的g值和从周围格子移动到目标格子的成本的最小值。因此，在初始状态下每个栅格的g值等于其rhs值。我们称这种格子为局部一致的。这个概念很重要，因为所有g值都等于相应的起始距离，如果所有单元都是局部一致的。

当地图中障碍物发生变化的时候，该格子的rhs值会发生改变。此时格子的g值跟rhs值会变的不一致。对于g值跟rhs值不一致的栅格，称为局部不一致栅格。这里同样分为两种情况：

1、原来是障碍物的栅格移除了障碍物，对于这种情况，我们称之为局部过一致，即：
$$g(s)>rhs(s)$$

2、原来空白的栅格添加了新的障碍物，对于这种情况，我们称之为局部欠一致，即：
$$g(s)<rhs(s)$$

对于这两点，还是比较好理解的。对于原来是障碍物的点，它的rhs值以及g值本来都是无穷大，在将障碍物移除后，会更新rhs值，则根据上面的公式我们可以知道该值一定是一个确定的值（除非它周围所有点的g值都是无穷）。而同样的，本来一个空白的格子其g值应该等与rhs值，但是当其变为障碍物时，它的rhs值也会变成无穷，也就满足了局部欠一致的条件。

对于这两个情况，算法会分为两种不同的处理方式：

对于局部过一致的点位，会将其g值更新为rhs值，并同时更新其周围点位信息。对于局部欠一致的点位，会将其g值更新为无穷大，然后更新其周围点的信息。对于这里的UpdateVertex函数，原论文是这么定义的：

简单的来说，算法对于每个栅格的更新主要分为三步：

1、更新这个格子的rhs值，它的值为其周围所有栅格中，其g值加上这个栅格到目标栅格的h值之和的最小值。

2、如果这个栅格属于集合U，则将其移除U集合，因为每次需要更新的点位都是从集合U中选取的，对于遍历过的点位自然要先移除。

3、如果这个点位的g值跟rhs值不一致，则重新将其插入集合U。注意插入后的点的U的值跟之前的值应该是不一样的。这里关于U的值的计算遵循下述公式：

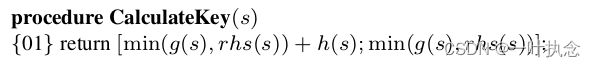
可以看到U其实是个两个数的集合，第一位数带了一步预测值，第二位数为其g值与rhs值中较小的那一个。

简单的来说，LPA* 的基本思想就是，首先利用A* 算法找到一条路径，同时维护每个栅格的两个值：g值与rhs值。然后在运动过程中，如果地图的障碍物发生变化，则更新其rhs值。此时g值与rhs值会不一致，这种栅格成为局部不一致栅格。然后算法通过ComputeShortestPath函数对这些局部不一致栅格进行处理，使其变得局部一致，在这个过程中也就找到了一条新的路径。

整个算法的总体原理流程图如下：

例子

讲了一堆，云里雾里，还是通过一个简单的例子来看一下这个问题：
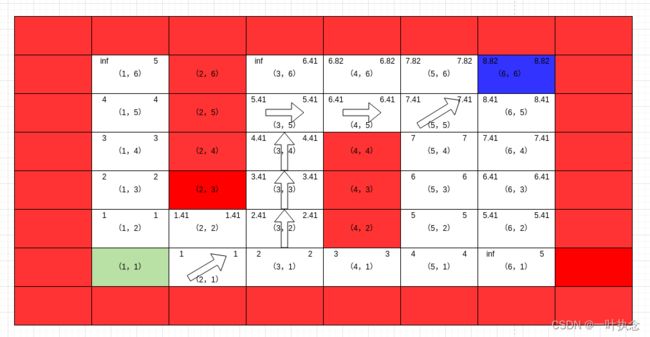
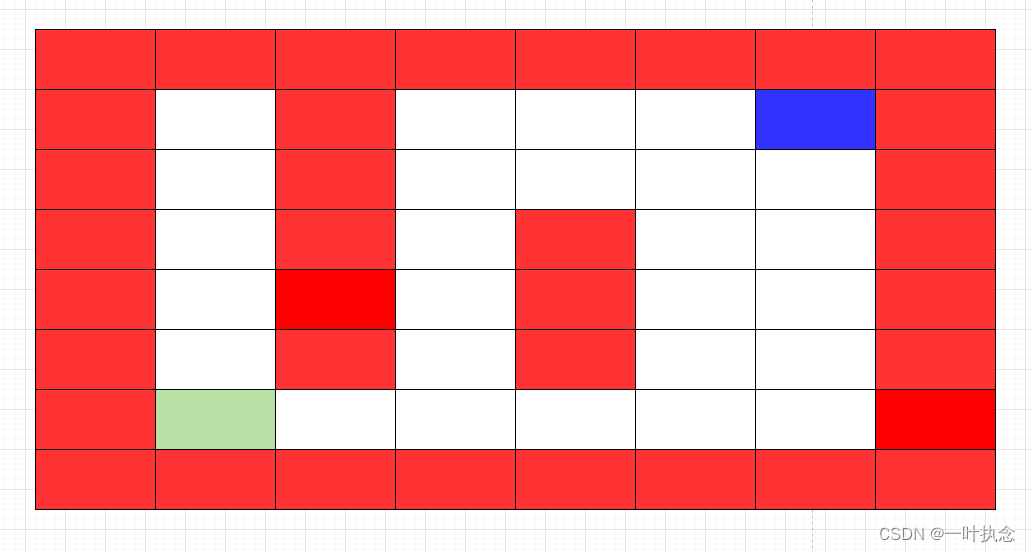假设我们有如上场景，左下角浅绿色为起点，蓝色格子为终点，红色为障碍物，初始时，采用A* 算法我们规划出一条路径如下：
同时我们得到每个栅格的g值与rhs值如下：

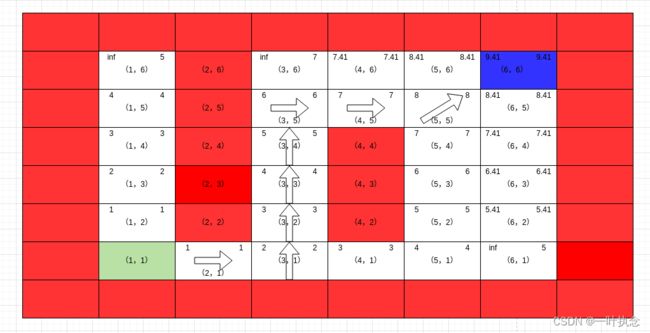
其中左上角为g值右上角为rsh值。注意这里有几个点的g值为inf但是rsh值是确定值，这里是因为在更新某个点的时候会更新其周围点的rsh值，但是g值则需要更新这个点的时候才会更新。而A* 可以说是带有方向性的，不是所有点都会被遍历，因此会出现这个问题。但是不影响算法实际的使用。

局部过一致处理流程：

假设我们将（2，2）处的障碍物移除。首先算法会更新该点的rhs值。其值更新遵循文章最上面的公式。因此其rhs值会变为1.41：

对于上面被修改过的点，会被放入集合U作为不一致点进行处理。然后算法会进入ComputeShortestPath函数，更新这些不一致点的g值与rhs值。更新时取出点的逻辑为先取处集合U中（min(g(s), rhs(s)) + h(s))值最小的点。因此首先被取处的是（2，2）,该点满足局部过一致条件，因此更新其g值等与rhs值。然后再更新其周围所有相邻点的值：
在这个过程中有两个点被修改了，首先修改的是（2，2）点的g值，其被修改为与rhs值一致。此时该点位回归为局部一致点位，会将其从U中剔除，同时由于之前的点位（3，2）的rhs值被修改为2.41小于其g值，所以该点变为局部不一致点位，加入集合U。

然后算法再次从U中取处点位（3，2），执行ComputeShortestPath函数：
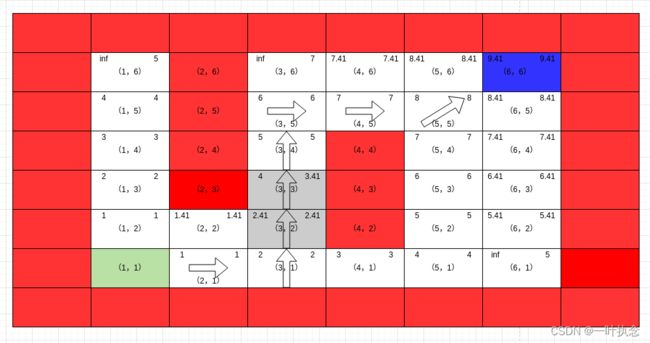这个过程点位（3，2）从集合U中删除，并将点位（3，3）加入集合。然后算法再次从U中取处点位（3，3），执行ComputeShortestPath函数：

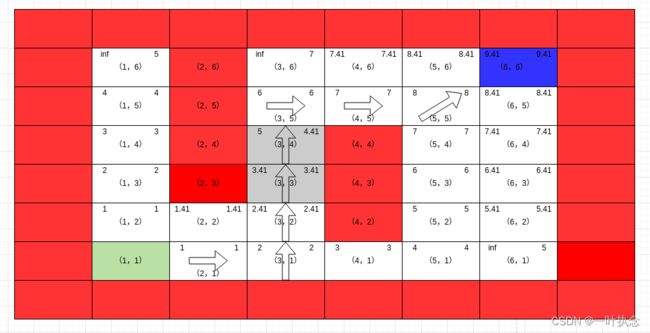
这个过程点位（3，3）从集合U中删除，并将点位（3，4）加入集合。然后算法再次从U中取处点位（3，4），执行ComputeShortestPath函数：

这个过程点位（3，4）从集合U中删除，并将点位（3，5）加入集合。然后算法再次从U中取处点位（3，5），执行ComputeShortestPath函数：
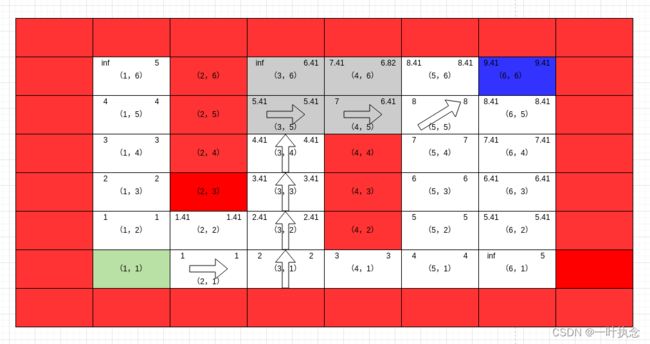这个过程点位（3，5）从集合U中删除，并将点位（3，6）、点位（4，5）、点位（4，6）加入集合。然后算法再次从U中取处点位（4，5），执行ComputeShortestPath函数：

这个过程点位（4，5）从集合U中删除，并将点位（5，5）、点位（5，6）加入集合。然后算法再次从U中取处点位（4，6），执行ComputeShortestPath函数：
这个过程点位（4，6）从集合U中删除，但是周围点的rhs值都被更新过了，所以这一步没有新的点位加入集合。然后算法再次从U中取处点位（5，5），执行ComputeShortestPath函数：

将点位（5，5）从集合U中删除，将点位（6，6）加入集合。算法再次从U中取处点位（5，6），执行ComputeShortestPath函数：
将点位（5，6）从集合U中删除，算法再次从U中取处点位（6，6），执行ComputeShortestPath函数：
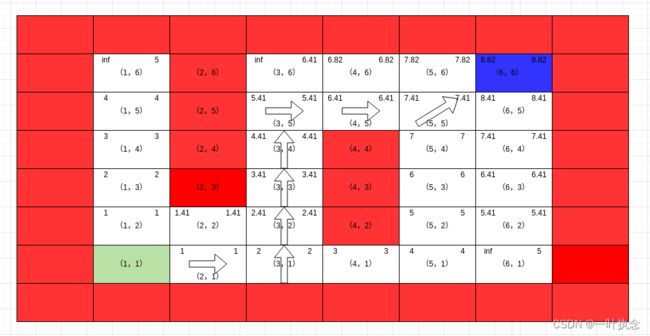此时这些点都再次恢复了局部一致性，注意到其实在这个过程中还是存在局部不一致点位的，例如（3，6）一直没有更新。但是此时ComputeShortestPath函数已经不满足了，所以算法跳出了。该点也就不需要再次更新了。

关于这里的判断，论文中是这么定义的：

所以对于点（3，6）而言，它的值应该为[9.41，6.41]。9.41为rhs(s)+h(s)的值。而终点的值为8.82小于9.41，所以（3，6）这个点怎么优化都不可能比现在的路径更短，自然不需要再更新了。

最后，我们可以得到更新后的路径为：

局部欠一致处理流程：

看完局部过一致流程，接下来我们再看一下局部欠一致处理流程。修改初始地图，假设初始时（2，2）点位为空白，得到地图路径为：

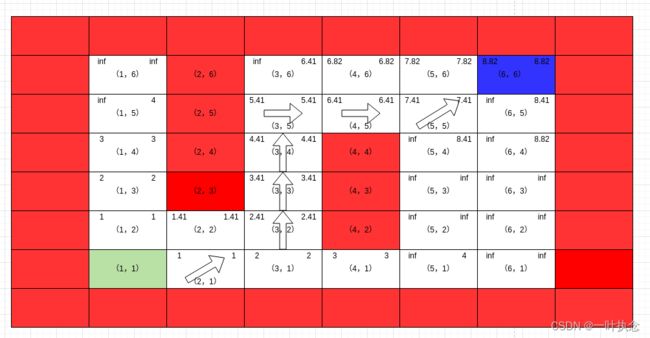
然后我们将（2，2）添加为障碍物，此时该点的rhs值为inf，然后将点位添加到集合U中，执行ComputeShortestPath函数：

此时点（3，2）的rhs值被修改为3，该点变为局部不一致点位，加入集合U，同时从集合U中剔除点位（2，2）,继续循环：
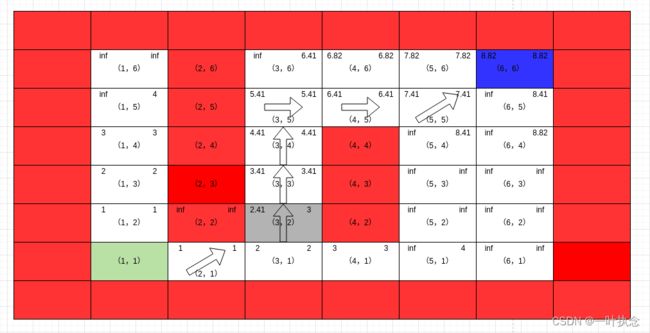根据ComputeShortestPath函数算法首先更新点（3，2）的g值，由于这个点是局部欠一致点位，所以其g值应该直接更新为inf，同时更新点（3，2）周围点的rhs值：

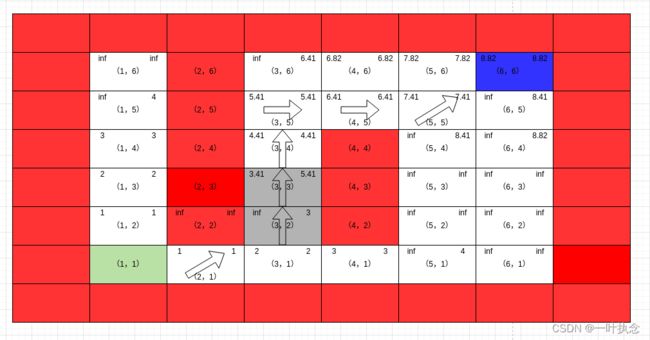然后更新点（3，3）的g值，同时更新点（3，3）周围点的rhs值：

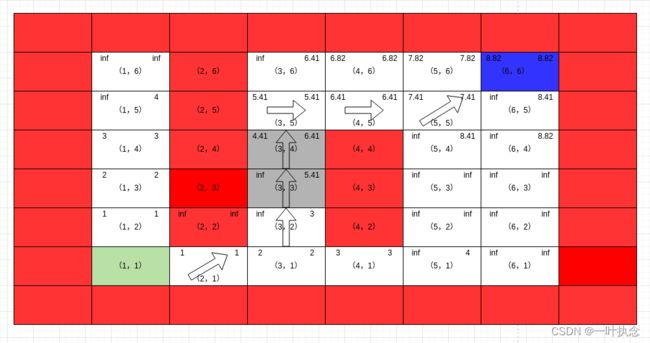然后更新点（3，2）的g值，同时更新点（4，3）周围点的rhs值：此时该点为过一致点，按照前面过一致点进行处理：
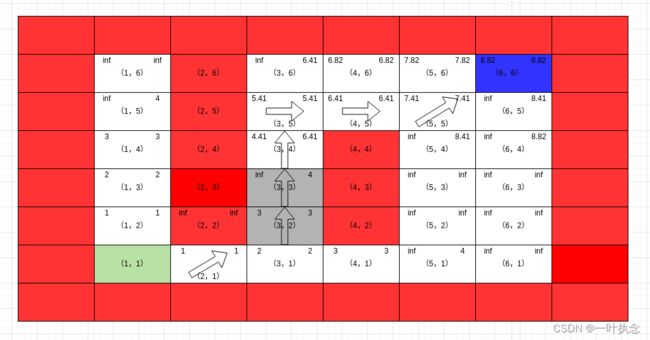这样子，点（2，2）与点（3，2）都恢复了局部一致性，然后更新点（3，4）：

然后处理点（3，3）：

然后处理点（3，5）：

然后处理点（3，4）：
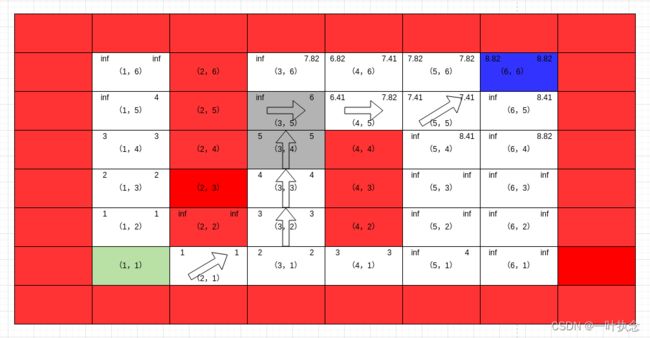然后处理点（4，5）：
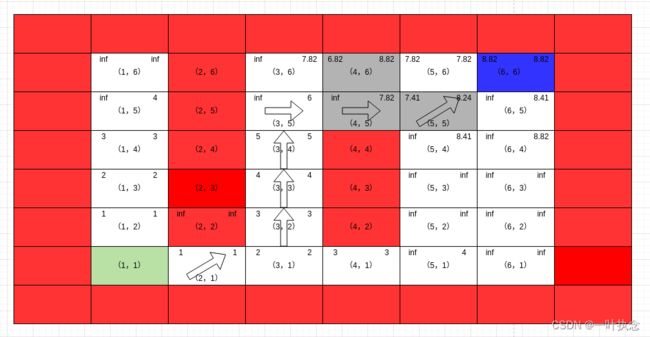然后处理点（4，6）：
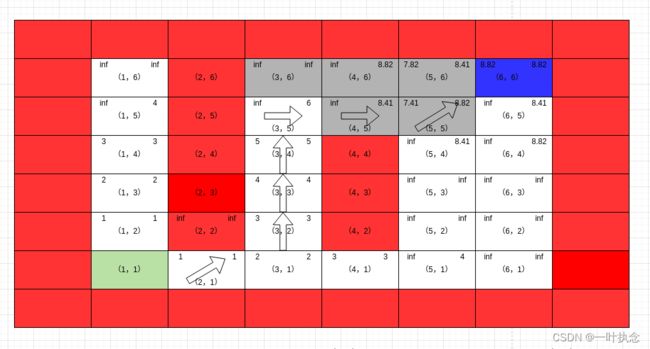然后处理点（5，5）：
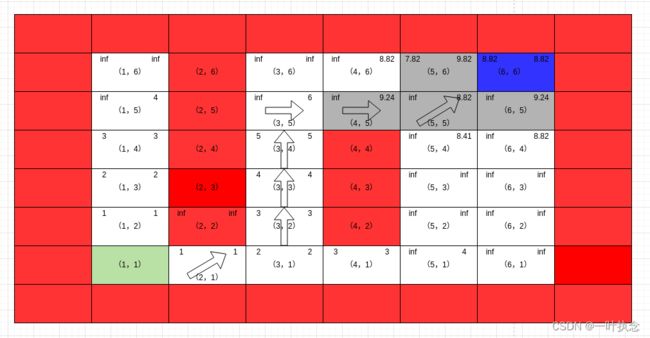然后处理点（5，6）：
然后处理点（6，6）：

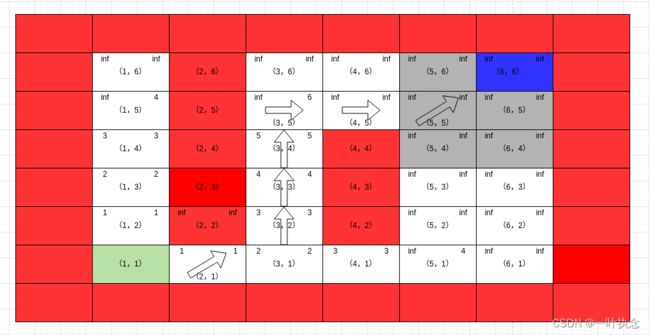
中间省略一部分迭代过程（1，5）》（5，1）》（5，2）》（3，5）》（5，3）》（4，5）》(5，4）》（6，2）》（6，3）》（4，6）》（6，4）》（5，5）》（5，6）》（6，5）》（6，6），得到最终结果为：

小结

总体来说LPA* 算法的思路就是使用两个列表维护每个栅格的值，当两个值不一致时，称该栅格为局部不一致，则根据ComputeShortestPath函数更新每个栅格的值，对于原来是障碍物后面消除的情况称为局部过一致点，处理起来会比较容易，对于原来是空白点位后面变成障碍物的称为局部欠一致点，处理情况会略微复杂一点，首先会将点变为局部过一致点，再按照局部过一致点的处理方式再处理一遍，最后达到点位的一致性，同时对于不一致点的遍历原则会类似于A* 算法的遍历方式，这样会提高点位的遍历效率。

代码实现：

import os
import sys
import math
import matplotlib.pyplot as plt

class LPAStar:
    def __init__(self, s_start, s_goal, heuristic_type,xI, xG):
        self.xI, self.xG = xI, xG
        self.x_range = 51  # size of background
        self.y_range = 31
        self.motions = [(-1, 0), (-1, 1), (0, 1), (1, 1),
                        (1, 0), (1, -1), (0, -1), (-1, -1)]  # feasible input set
        self.obs = self.obs_map()
        self.s_start, self.s_goal = s_start, s_goal
        self.heuristic_type = heuristic_type
        self.u_set = self.motions
        self.obs = self.obs
        self.x = self.x_range
        self.y = self.y_range

        self.g, self.rhs, self.U = {}, {}, {}

        for i in range(self.x_range):
            for j in range(self.y_range):
                self.rhs[(i, j)] = float("inf")
                self.g[(i, j)] = float("inf")

        self.rhs[self.s_start] = 0
        self.U[self.s_start] = self.CalculateKey(self.s_start)
        self.visited = set()
        self.count = 0

        self.fig = plt.figure()

    def obs_map(self):
        """
        Initialize obstacles' positions
        :return: map of obstacles
        """

        x = 51
        y = 31
        obs = set()

        for i in range(x):
            obs.add((i, 0))
        for i in range(x):
            obs.add((i, y - 1))

        for i in range(y):
            obs.add((0, i))
        for i in range(y):
            obs.add((x - 1, i))

        for i in range(10, 21):
            obs.add((i, 15))
        for i in range(15):
            obs.add((20, i))

        for i in range(15, 30):
            obs.add((30, i))
        for i in range(16):
            obs.add((40, i))

        return obs
    def update_obs(self, obs):
        self.obs = obs


    def plot_grid(self, name):
        obs_x = [x[0] for x in self.obs]
        obs_y = [x[1] for x in self.obs]

        plt.plot(self.xI[0], self.xI[1], "bs")
        plt.plot(self.xG[0], self.xG[1], "gs")
        plt.plot(obs_x, obs_y, "sk")
        plt.title(name)
        plt.axis("equal")
    def plot_path(self, path, cl='r', flag=False):
        path_x = [path[i][0] for i in range(len(path))]
        path_y = [path[i][1] for i in range(len(path))]

        if not flag:
            plt.plot(path_x, path_y, linewidth='3', color='r')
        else:
            plt.plot(path_x, path_y, linewidth='3', color=cl)

        plt.plot(self.xI[0], self.xI[1], "bs")
        plt.plot(self.xG[0], self.xG[1], "gs")

        plt.pause(0.01)


    def run(self):
        self.plot_grid("Lifelong Planning A*")

        self.ComputeShortestPath()
        self.plot_path(self.extract_path())
        self.fig.canvas.mpl_connect('button_press_event', self.on_press)

        plt.show()

    def on_press(self, event):
        x, y = event.xdata, event.ydata
        if x < 0 or x > self.x - 1 or y < 0 or y > self.y - 1:
            print("Please choose right area!")
        else:
            x, y = int(x), int(y)
            print("Change position: s =", x, ",", "y =", y)

            self.visited = set()
            self.count += 1

            if (x, y) not in self.obs:
                self.obs.add((x, y))
                self.UpdateVertex((x, y))
            else:
                self.obs.remove((x, y))
                self.UpdateVertex((x, y))

            self.update_obs(self.obs)

            #for s_n in self.get_neighbor((x, y)):
            #    self.UpdateVertex(s_n)

            self.ComputeShortestPath()
            
            plt.cla()
            self.plot_grid("Lifelong Planning A*")
            self.plot_visited(self.visited)
            self.plot_path(self.extract_path())
            self.fig.canvas.draw_idle()

    def ComputeShortestPath(self):
        while True:
            s, v = self.TopKey()
            if v >= self.CalculateKey(self.s_goal) and \
                    self.rhs[self.s_goal] == self.g[self.s_goal]:
                break

            self.U.pop(s)
            self.visited.add(s)
            
            if self.g[s] > self.rhs[s]:

                # Condition: over-consistent (eg: deleted obstacles)
                # So, rhs[s] decreased -- > rhs[s] < g[s]
                self.g[s] = self.rhs[s]
            else:

                # Condition: # under-consistent (eg: added obstacles)
                # So, rhs[s] increased --> rhs[s] > g[s]
                self.g[s] = float("inf")
                self.UpdateVertex(s)

            for s_n in self.get_neighbor(s):
                self.UpdateVertex(s_n)

    def UpdateVertex(self, s):
        """
        update the status and the current cost to come of state s.
        :param s: state s
        """

        if s != self.s_start:

            # Condition: cost of parent of s changed
            # Since we do not record the children of a state, we need to enumerate its neighbors
            self.rhs[s] = min(self.g[s_n] + self.cost(s_n, s)
                              for s_n in self.get_neighbor(s))

        if s in self.U:
            self.U.pop(s)

        if self.g[s] != self.rhs[s]:

            # Condition: current cost to come is different to that of last time
            # state s should be added into OPEN set (set U)
            self.U[s] = self.CalculateKey(s)
            #print(self.U[s])

    def TopKey(self):
        """
        :return: return the min key and its value.
        """

        s = min(self.U, key=self.U.get)

        return s, self.U[s]

    def CalculateKey(self, s):

        return [min(self.g[s], self.rhs[s]) + self.h(s),
                min(self.g[s], self.rhs[s])]

    def get_neighbor(self, s):
        """
        find neighbors of state s that not in obstacles.
        :param s: state
        :return: neighbors
        """

        s_list = set()

        for u in self.u_set:
            s_next = tuple([s[i] + u[i] for i in range(2)])
            if s_next not in self.obs:
                s_list.add(s_next)

        return s_list

    def h(self, s):
        """
        Calculate heuristic.
        :param s: current node (state)
        :return: heuristic function value
        """

        heuristic_type = self.heuristic_type  # heuristic type
        goal = self.s_goal  # goal node

        if heuristic_type == "manhattan":
            return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
        else:
            return math.hypot(goal[0] - s[0], goal[1] - s[1])

    def cost(self, s_start, s_goal):
        """
        Calculate Cost for this motion
        :param s_start: starting node
        :param s_goal: end node
        :return:  Cost for this motion
        :note: Cost function could be more complicate!
        """

        if self.is_collision(s_start, s_goal):
            return float("inf")

        return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])

    def is_collision(self, s_start, s_end):
        if s_start in self.obs or s_end in self.obs:
            return True

        if s_start[0] != s_end[0] and s_start[1] != s_end[1]:
            if s_end[0] - s_start[0] == s_start[1] - s_end[1]:
                s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
                s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
            else:
                s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
                s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))

            if s1 in self.obs or s2 in self.obs:
                return True

        return False

    def extract_path(self):
        """
        Extract the path based on the PARENT set.
        :return: The planning path
        """

        path = [self.s_goal]
        s = self.s_goal

        for k in range(100):
            g_list = {}
            for x in self.get_neighbor(s):
                if not self.is_collision(s, x):
                    g_list[x] = self.g[x]
            s = min(g_list, key=g_list.get)
            path.append(s)
            if s == self.s_start:
                break

        return list(reversed(path))

    def plot_path(self, path):
        px = [x[0] for x in path]
        py = [x[1] for x in path]
        plt.plot(px, py, linewidth=2)
        plt.plot(self.s_start[0], self.s_start[1], "bs")
        plt.plot(self.s_goal[0], self.s_goal[1], "gs")

    def plot_visited(self, visited):
        color = ['gainsboro', 'lightgray', 'silver', 'darkgray',
                 'bisque', 'navajowhite', 'moccasin', 'wheat',
                 'powderblue', 'skyblue', 'lightskyblue', 'cornflowerblue']

        if self.count >= len(color) - 1:
            self.count = 0

        for x in visited:
            plt.plot(x[0], x[1], marker='s', color=color[self.count])


def main():
    x_start = (5, 5)
    x_goal = (45, 25)

    lpastar = LPAStar(x_start, x_goal, "Euclidean",x_start,x_goal)
    lpastar.run()


if __name__ == '__main__':
    main()

初始状态下规划结果为：

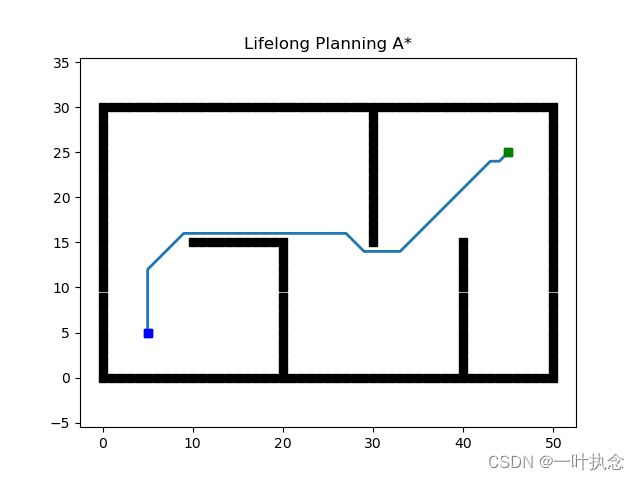
消除某个障碍物：

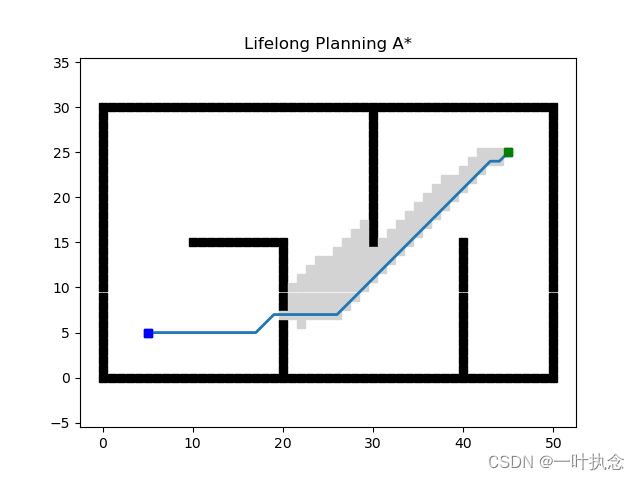
添加一个新的障碍物：

参考：
1、《终身规划A算法（LPA）：Lifelong Planning A*》
2、《LPA* 路径搜索算法介绍及完整代码》
3、《路径规划算法》