强化学习拾遗 —— 表格型方法和函数近似方法中 Bellman 迭代的收敛性分析

因为想申请 CSDN 博客认证需要一定的粉丝量，而我写了五年博客才 700 多粉丝，本文开启关注才可阅读全文，很抱歉影响您的阅读体验

• 本文讨论两个主要内容
  1. 表格型 policy evaluation 方法中，使用 Bellman 算子/Bellman 最优算子进行迭代的收敛性
  2. 使用函数近似方法进行 policy evaluation 时的收敛性问题
• 首先补充一点测度论中的定义，然后介绍压缩映射原理和不动点，最后证明收敛性。

---

1. 基础概念

1.1 测度论概念补充

• 注：本人没有学过测度论，就临时看了一下概念，因此这一段不甚准确，具体请参考程士宏《测度论和概率论基础》
• 测度论其实是概率论的基础，但是二者可以独立开来讲，本科阶段学习的概率论课程通过公理化定义回避了这些底层的内容，可一旦进入随机过程这些更深入的课程后，有些问题离开测度论是无法考虑的。测度论致力于在抽象空间建立类似实变函数中测度、积分和导数那样的分析系统，下面简单捋一下部分关键概念

  1. 空间：任给一个非空集合 $X$，称之为空间

  2. 集合：$X$ 的子集称为集合，用大写字母 $A,B,C...$ 表示

  3. 元素：$X$ 的成员称为元素，用小写字母 $x,y,z...$ 表示，元素可以被某个集合包含，如 $x\in A$

  4. 集合系：以空间 $X$ 中一些集合为元素组成的集合称为 $X$ 上的集合系，用花体字母 $\mathcal{A},\mathcal{B},\mathcal{C}...$ 表示

  5. σ域/σ代数：一种特殊的集合系 $\mathcal{F}$，满足以下性质

     1. $X\in \mathcal{F}$
     2. $A\in \mathcal{F}\Rightarrow A^c\in \mathcal{F}$，其中 $A^c$ 是集合 $A$ 的补集
     3. $A_n\in \mathcal{F},n=1,2,...\Rightarrow {\bigcup }_{n=1}^{\infty }{A}_n\in \mathcal{F}$

     就是说 $\sigma$ 域上的集合关于集合的补和并封闭，是一种要求很强的集合系，下图表现了不同集合系从宽松到严格的顺序
     
     我们最关注 $\sigma$ 域，因为其性质允许我们建立测度

  6. 可测空间：非空集合 $X$ 和其上的一个 $\sigma$ 域放在一起组成可测空间 $(X,\mathcal{F})$

  7. 生成σ域：由集合系 $\mathcal{E}$ 生成的 $\sigma$ 域 $\mathcal{S}$，是包含 $\mathcal{E}$ 的最小的 $\sigma$ 域，满足

     1. $\mathcal{S}\supset \mathcal{E}$
     2. 对任意 $\sigma$ 域 ${\mathcal{S}}^{\prime }$ 都有 ${\mathcal{S}}^{\prime }\supset \mathcal{E}\Rightarrow {\mathcal{S}}^{\prime }\supset \mathcal{S}$

     这种由集合系生成的 $\sigma$ 域记作 $\sigma (\mathcal{E})$

  8. 映射：设 $X$ 和 $Y$ 是任意给定的集合，若对每个 $x\in X$，存在唯一的 $f(x)\in Y$ 与之对应， 则称 $f$ 是从 $X$ 到 $Y$ 的映射

  9. 原像：$\forall B\in Y$ 集合 $B$ 在映射 $f$ 下的原像为
     $$f^{-1}B:=\{x:f(x)\in B\}$$ $\forall \mathcal{E}\in Y$，集合系 $\mathcal{E}$ 在映射 $f$ 下的原像为其包含所有集合的原像的集合
     $$f^{-1}\mathcal{E}:=\{f^{-1}B:B\in \mathcal{F}\}$$ 可证明 $Y$ 上的任何集合系 $\mathcal{E}$ 有 $\sigma (f^{-1}\mathcal{E})=f^{-1}\sigma (\mathcal{E})$

  10. 可测映射/随机元 & 使映射可测的最小σ域：给定可测空间 $(X,\mathcal{F})$ 到 $(Y,\mathcal{S})$ 以及 $X$ 到 $Y$ 的映射 $f$，若
      $$f^{-1}\mathcal{S}\subset \mathcal{F}$$ 则称 $f$ 为从 $(X,\mathcal{F})$ 到 $(Y,\mathcal{S})$ 的可测映射或随机元；$\sigma (f):=f^{-1}\mathcal{S}$ 叫做使映射 $f$ 可测的最小 $\sigma$ 域。这个东西的意义在于，假设我们在 $(X,\mathcal{F})$ 上面定义了一个测度（比如集合的大小），那么对于 $(Y,\mathcal{S})$ 中的任意元素 $y\in \mathcal{S}$，都能通过 $f$ 找到其在 $\mathcal{F}$ 上的原像，从而得到其对应的在 $(X,\mathcal{F})$ 上的测度值

  11. 广义实数集 $\bar{R}:=R\cup \{-\infty ,+\infty \}$，并且从普通实数集生成其对应的 $\sigma$ 域 ${\mathcal{B}}_{\bar{R}}:=\sigma ({\mathcal{B}}_R,\{-\infty ,+\infty \})$（这个准确说叫 Borel 系）

  12. 可测函数 & 有限可测函数/随机变量：从可测空间 $(X,\mathcal{F})$ 到 $(\bar{R},{\mathcal{B}}_{\bar{R}})$ 的可测映射称为 $(X,\mathcal{F})$ 上的可测函数；特别的，从可测空间 $(X,\mathcal{F})$ 到 $(R,{\mathcal{B}}_R)$ 的可测映射称为 $(X,\mathcal{F})$ 上的有限可测函数/随机变量。这个的意义在于把集合系上的抽象元素映射成实数了，这样就方便我们使用高数工具进行操作，这有点像矩阵论中把向量空间中一个向量转换为它在一组基下的对应的数的坐标

  13. 非负集函数：给定空间 $X$ 上的集合系 $\mathcal{E}$，定义在 $\mathcal{E}$ 上，取值于 $[0,\infty ]$ 的函数称为非负集函数，记为 $\mu ,\nu ,\tau ...$

  14. 可列可加性：设 $\mu$ 是 $\mathcal{E}$ 上的非负集函数，若对于任意可列个两两不交的集合 $A_1,A_2,...,A_n$， 只要 ${\bigcup }_{n=1}^{\infty }{A}_n\in \mathcal{E}$，就一定有
      $$\mu (\bigcup _{n=1}^{\infty }{A}_n)=\sum _{n=1}^{\infty }\mu (A_n)$$ 则称 $\mu$ 具有可列可加性。举例来说，面积作为一种测度具有可列可加性，可以看作上式的 $\mu$，当我们要测量一个不规则图形面积时，可以用矩形不断对其进行分割，并且用越来越小的矩形去逼近边缘，最后把所有画出的矩形面积求和得到估计值

  15. 测度：设 $\mathcal{E}$ 是 $X$ 上的集合系且 $\varnothing \notin \mathcal{E}$，若 $\mathcal{E}$ 上的非负集函数 $\mu$ 有可列可加性且满足 $\mu (\varnothing )=0$，则称之为 $\mathcal{E}$ 上的测度

      1. 若对于每个 $A\in \mathcal{E}$ 还有 $\mu (A)<\infty$，则称测度是有限的；
      2. 若对于每个 $A\in \mathcal{E}$ 存在满足 $\mu (A)<\infty$ 的 $\{A_n\in \mathcal{E},n=1,2,...\}$，则称测度是σ有限的

  16. 测度空间：虽然前面在很一般的角度上定义了测度，但我们的主要目标还是讨论由 $X$ 的子集生成的某个 $\sigma$ 域 $\mathcal{F}$ 上的测度。我们把空间 $X$，加上由其子集生成的某个 $\sigma$ 域 $\mathcal{F}$，再加上 $\mathcal{F}$ 上的一个测度 $\mu$，三者组成的 $(X,\mathcal{F},\mu )$ 称为测度空间

      如果测度空间 $(X,\mathcal{F},P)$ 满足 $P(X)=1$，则称它为 概率空间，对应的 $P$ 称为 概率测度，$\mathcal{F}$ 中的集合 $A$ 称为 事件，而 $P(A)$ 称为事件 $A$ 发生的 概率

  17. Lp空间：设 $(X,\mathcal{F},\mu )$ 是测度空间且 $1\le p<\infty$，用 $L_p(X,\mathcal{F},\mu )$ 表示 $(X,\mathcal{F},\mu )$ 上全体模 $p$ 阶可积的可测函数 $f$ 的集合，即满足
      $${\int }_X|f{|}^{p}d\mu <\infty$$ 由于只考虑给定测度空间上的集合，故 $L_p(X,\mathcal{F},\mu )$ 简记为 $L_p$，其本质是一个赋范向量空间，具有以下性质

      1. 对空间中元素（即映射 $f$）定义了范数：范数是从指定空间到实属的映射关系，具有非负性、其次性并满足三角不等式，引入范数意味着空间具有了长度与距离的概念

      2. 具有完备性：这个概念比较绕，我们和欧拉空间做类比

         粗略但是直观的说，完备是指空间中没有任何遗漏的点。而想要理解 “没有遗漏的点” 这个概念需要用到距离，一个空间需要定义距离，完备才变得有意义。从实数空间入手，我们说实数空间 R 是完备的，在实数空间中，距离的定义是两元素差的绝对值，可以想想看，任何一个点在与它距离趋近为0的地方都存在一个点并且这个点是在实数空间中的，因此我们说实数空间是完备的

         完备性的具体定义需要借助柯西序列，请参考 机器学习的数学基础（2）：赋范空间、内积空间、完备空间与希尔伯特空间

      3. $L^p$ 空间又称 Lebesgue空间，其中的函数 $f$ 都是 Lebesgue可积的，这里可参考 泛函分析笔记(八)Banach 空间中的lp空间和Lebesgue空间 (勒贝格空间)

      说白了就是空间中一些具有特殊性质的测度的集合

1.2 收缩映射定理

• 收缩映射 Contraction Mapping：收缩映射 $T:L^p\to L^p$ 是定义在 $L_p$ 空间上的映射，满足 $\forall f,g\in T^p$ 有
  $$||T(f)-T(g)|{|}_{\rho }\le c||f-g|{|}_{\rho },(0\le c<1)$$ 其中 $||\cdot |{|}_{\rho }$ 是 $\rho$-范数，可以把它看作一种距离度量，也就是说原先的两个可测函数 $f,g$ 经过收缩映射后距离减小了
  
  如果其中 $T$ 是微分算子，则称压缩映射 $T$ 是满足 Lipschitz 条件的映射

• 收缩映射定理：若 $T$ 是 $L^p$ 空间上的收缩映射，则方程
  $$(T-I)(f)=0\iff T(f)=f$$ 在 $L^p$ 空间内仅有一个 $f$ 解，称之为 $L^p$ 内 $T$ 的 不动点。注意到若 $T$ 是微分算子，则上式为一个常微分方程，因此收缩映射定理常用于证明常微分方程解的存在性和唯一性。从几何意义上看，$T$ 将 $f$ 映射回自身
  

• 压缩映射原理的证明思路如下：

  1. 首先任选 $f_0\in L^p$，然后反复使用 $T$ 进行映射得到一个无穷的序列
     $$f_1=T(f_0),f_2=T(f_1),...,f_n=T(f_{n-1}),...$$
  2. 注意到由于来自压缩映射，其中任意相邻两项距离度量越来越近，即 $\{f\}$ 是一个柯西序列，由于 $L^p$ 空间具有完备性，该序列必然收敛到 $L^p$ 内部，这说明不动点 ${\lim }_{n\to \infty }{f}_n$ 一定存在
  3. 最后考虑 $T(f_0)$ 是否收敛回 $f_0$ 自身，这只须证明 ${\lim }_{n\to \infty }||f_n-f_0||=0$ 即可，我们利用范数的三角不等式，不断向 $f_n$ 和 $f_0$ 之间插入 $f_i$，并结合柯西序列性质进行放缩，最后即可得证不动点一定唯一，且为 ${\lim }_{n\to \infty }{f}_n=f_0$

  详细证明流程可以参考 压缩映射不动点定理

2. 表格型 Bellman 迭代的收敛性证明

• 考察 MDP 中全体 $s$ 或 $(s,a)$ 组成的空间 $X$ 及其自身组成的集合系 $\mathcal{F}=X$，显然其上的子集合关于集合的补和并封闭，故这也是一个 $\sigma$ 域，这样 $(X,\mathcal{F})$ 就组成测度空间，价值函数 $V(s)$ 和 $Q(s,a)$ 将其中的元素映射为实数，属于可测函数，因此 $V,Q\in L^p$
• 下面利用上述压缩映射原理来证明常见的两种 Bellman 迭代的收敛性，只需证明两种 Bellman 算子都是压缩映射

  注意：以下分析是基于 model-based 情况的，即状态转移矩阵和奖励函数已知。对于 model-free 情况（使用 TD 方法）收敛性仍然成立，但要求估计更新步长满足随机近似条件

2.1 Bellman operator 的收敛性

• 先考察关于策略 $\pi$ 的 Bellman 算子 ${\mathcal{B}}_{\pi }$，该算子应用于 model-based 的 evaluation 方法 policy evaluation
  $$({\mathcal{B}}_{\pi }U)(s):=\sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)[r(s,a,s^{\prime })+\gamma U(s^{\prime })]$$ $\forall s,s^{\prime },s^{\prime \prime }\in \mathcal{S},a\in \mathcal{A}$，对于任意两个价值函数 $U_1(s),U_2(s)$，考察映射后二者距离
  $$\begin{array}{rl}|({\mathcal{B}}_{\pi }{U}_1)(s)-({\mathcal{B}}_{\pi }{U}_2)(s)|& =|\sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)\gamma [U_1(s^{\prime })-U_2(s^{\prime })]|\\ & \le \gamma \sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)|U_1(s^{\prime })-U_2(s^{\prime })|\\ & \le \gamma \sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)(\underset{s^{\prime \prime }}{\max }|U_1(s^{\prime \prime })-U_2(s^{\prime \prime })|)\\ & =\gamma \underset{s^{\prime \prime }}{\max }|U_1(s^{\prime \prime })-U_2(s^{\prime \prime })|\\ & =\gamma ||U_1-U_2|{|}_{\infty }\end{array}$$ 注意到对于任意 $s\in \mathcal{S}$ 上式都成立，故对 $s={\mathrm{argmax}}_s|({\mathcal{B}}_{\pi }{U}_1)(s)-({\mathcal{B}}_{\pi }{U}_2)(s)|$ 也成立，即有
  $$||{\mathcal{B}}_{\pi }{U}_1-{\mathcal{B}}_{\pi }{U}_2|{|}_{\infty }\le \gamma ||U_1-U_2|{|}_{\infty }$$ 因此 Bellman 算子是一个压缩映射，根据收缩映射定理，policy evaluation 一定能收敛到唯一的价值函数 $V(s)$ 或 $Q(s,a)$

2.2 Bellman optimal operator 的收敛性

• 进一步考察 Bellman 最优算子 ${\mathcal{B}}^{\ast }$，该算子应用于 model-based 的 evaluation 方法 value iteration
  $$({\mathcal{B}}^{\ast }U)(s,a):=r(s,a)+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)\underset{a^{\prime }}{\max }U(s^{\prime },a^{\prime })$$ $\forall s,s^{\prime },s^{\prime \prime }\in \mathcal{S},a,a^{\prime },a_1^{\prime },a_2^{\prime }\in \mathcal{A}$，对于任意两个价值函数 $U_1(s,a),U_2(s,a)$，考察映射后二者距离
  $$\begin{array}{rl}|({\mathcal{B}}^{\ast }{U}_1)(s,a)-({\mathcal{B}}^{\ast }{U}_2)(s,a)|& =|\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)[\underset{a_1^{\prime }}{\max }{U}_1(s^{\prime },a_1^{\prime })-\underset{a_2^{\prime }}{\max }{U}_2(s^{\prime },a_2^{\prime })]|\\ & \le \gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)|\underset{a_1^{\prime }}{\max }{U}_1(s^{\prime },a_1^{\prime })-\underset{a_2^{\prime }}{\max }{U}_2(s^{\prime },a_2^{\prime })|\\ & \le \gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)|\underset{a^{\prime }}{\max }(U_1(s^{\prime },a^{\prime }))-U_2(s^{\prime },a^{\prime })|\\ & \le \gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)\underset{a^{\prime }}{\max }|U_1(s^{\prime },a^{\prime })-U_2(s^{\prime },a^{\prime })|\\ & \le \gamma \underset{s^{\prime \prime },a^{\prime \prime }}{\max }|U_1(s^{\prime \prime },a^{\prime \prime })-U_2(s^{\prime \prime },a^{\prime \prime })|\\ & =\gamma ||U_1-U_2|{|}_{\infty }\end{array}$$ 注意到对于任意 $s\in \mathcal{S},a\in \mathcal{A}$ 上式都成立，故对 $s,a={\mathrm{argmax}}_{s,a}|({\mathcal{B}}^{\ast }{U}_1)(s,a)-({\mathcal{B}}^{\ast }{U}_2)(s,a)|$ 也成立，即有
  $$||{\mathcal{B}}^{\ast }{U}_1-{\mathcal{B}}^{\ast }{U}_2|{|}_{\infty }\le \gamma ||U_1-U_2|{|}_{\infty }$$ 因此 Bellman optimal operator 也是一个压缩映射，根据收缩映射定理，value iteration 一定能收敛到唯一的最优价值函数 $V^{\ast }(s)$ 或 $Q^{\ast }(s,a)$

3. 函数近似法的收敛性问题

• 本段参考：CS294-112 at UC Berkeley

• 当使用函数近似法估计价值时，往往不会收敛，本节以 DQN 类算法中的价值网络为例进行分析，该类价值网络基于 Bellman optimal equation 进行优化，其损失函数设计为 TD error 的 L2 损失，通过优化该损失减小 TD error，使价值估计靠近 TD target。关于 DQN 论文的详解，请参考：论文理解【RL经典】 —— 【DQN】Human-level control through deep reinforcement learning

  注意：以下分析是基于 model-free 情况的

• 现在我们要优化以 $\varphi$ 参数化的 DQN 类价值网络 $V_{\varphi }$ ，其训练过程可以看做反复执行以下两步

  1. 计算样本的 TD target，即对于样本 $i$ 计算 $$y_i\leftarrow \underset{a_i}{\max }(r(s_i,a_i)+\gamma \mathbb{E}[V_{\varphi }(s_i^{\prime })])$$ 此步可以看做使用 Bellman optimal operator ${\mathcal{B}}^{\ast }$ 进行一步更新，即
     $$V\leftarrow {\mathcal{B}}^{\ast }V$$
  2. 执行一步 L2 损失回归，更新网络参数 $\varphi$，即 $$\varphi \leftarrow \underset{\varphi }{\mathrm{argmin}}\frac{1}{2}\sum _i||V_{\varphi }(s_i)-y_i|{|}^2$$注意这是一步学习过程，确定了一个参数 $\varphi$，就唯一地确定了一个新的网络价值 $V^{\prime }$，如果价值我们的函数逼近器的假设空间为 $\Omega$，这一步等价于在 $\Omega$ 中找出了一个 $V^{\prime }$，即
     $$V^{\prime }\leftarrow \underset{V^{\prime }\in \Omega }{\mathrm{argmin}}\frac{1}{2}\sum ||V^{\prime }(s)-({\mathcal{B}}^{\ast }V)(s)|{|}^2$$ 仔细分析这一步最小二乘回归，我们知道最小二乘回归等价于做向量空间投影（可参考 一文看懂最小二乘法），因此这一步可以看作在 $\Omega$ 空间中找出一个距离 ${\mathcal{B}}^{\ast }V$ 最近的点，不妨使用一个投影算子 $\Pi$ 来表示它
     $$\Pi :\Pi V=\underset{V^{\prime }\in \Omega }{\mathrm{argmin}}\frac{1}{2}\sum ||V^{\prime }(s)-V(s)|{|}^2$$

  综上所述，DQN 类算法中的价值网络，其训练过程可以看做使用 $\Pi {\mathcal{B}}^{\ast }$ 算子进行反复迭代，即
  $$V\leftarrow \Pi {\mathcal{B}}^{\ast }V$$

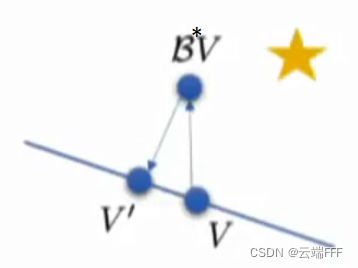
• 接下来考虑函数近似模型的表示能力，我们知道目前最强的函数近似工具，也就是神经网络，在参数量无穷的情况下可以近似任意函数，这时 $\Omega$ 空间是无限大的；但当参数有限时，无论使用什么模型，都只能表示有限大小的假设空间 $\Omega$，不妨使用二维空间中的一条直线来表示 $\Omega$，则使用 $\Pi {\mathcal{B}}^{\ast }$ 算子的一步更新可以表示如下
  

  观察一下发生了什么

  1. 假设神经网络随机初始化，则价值网络初始化为 $\Omega$ 上任意一点 $V$
  2. 使用 ${\mathcal{B}}^{\ast }$ 进行一步更新，这时 ${\mathcal{B}}^{\ast }V$ 仍在 $L^p$ 空间内，但是不一定还在 $\Omega$ 空间中了
  3. 使用 $\Pi$ 算子做一步投影，回到 $\Omega$ 空间上的 $V^{\prime }$

• 再考察一下这里的两个算子 ${\mathcal{B}}^{\ast }$ 和 $\Pi$

  1. ${\mathcal{B}}^{\ast }$：由 2.2 节，${\mathcal{B}}^{\ast }$ 关于无穷范数 $||\cdot |{|}_{\infty }$ 是压缩映射
  2. $\Pi$：投影本质上相当于对样本的某些维度进行压缩，两个点在投影前后的距离度量一定是收缩的，如下图所示
     
     显然投影后两个样本点的欧式距离肯定是减小的，$\Pi$ 关于 2范数 $||\cdot |{|}^2$ 范数是压缩映射，

• 两个算子单独看都能得到压缩映射，性质都很好，但是一旦把它们组合起来，$\Pi {\mathcal{B}}^{\ast }$ 不能关于任何范数成为压缩映射，这意味着迭代过程中，两个算子都会在各自的距离度量上将 $f,g$ 拉近，但同时很可能会在对方的距离度量上将 $f,g$ 推远，收敛性无法保证。举例来说，如下图所示，目标位置是星星处，一次迭代后得到的价值估计反而离目标更远了