AVL树
欢迎来到Cefler的博客
博客主页:那个传说中的man的主页
个人专栏:题目解析
推荐文章:题目大解析(3)
目录
- AVL树概念
- AVL树模拟实现
-
- insert插入
-
- 左旋
- 右旋
- 双旋:先右单旋再左单旋
- 双旋:先左单旋后右旋转
- 判断是否为平衡树
- AVLTree.h
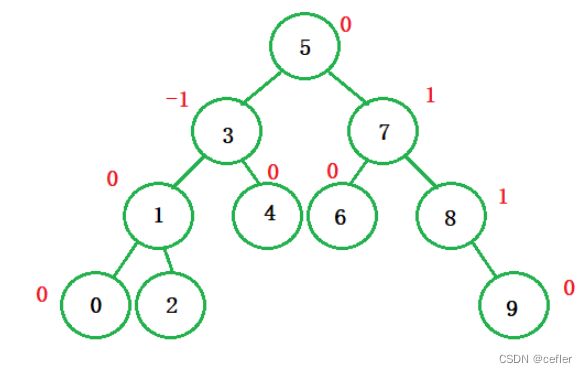
AVL树概念
AVL树是一种自平衡二叉搜索树,它在插入和删除操作后会通过旋转操作来保持树的平衡。它得名于发明者Adelson-Velsky和Landis。
AVL树的特点是,对于任意节点,其左子树的高度与右子树的高度之差(即平衡因子)不超过1。当插入或删除操作导致某个节点的平衡因子超过1时,就需要进行旋转操作来调整树的结构,使之重新满足平衡条件。
A V L 树的性质如下 AVL树的性质如下 AVL树的性质如下:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
平衡因子
1:左边矮,右边高
0:一样高
-1:左边高,右边矮
AVL树的旋转操作分为两种:左旋和右旋。左旋用于处理左子树过深的情况,而右旋用于处理右子树过深的情况。通过这两种旋转操作的组合,可以实现AVL树的自平衡。
插入元素时,先按照二叉搜索树的规则找到插入位置,并将新节点插入为叶子节点。然后,从插入位置向上回溯,更新每个祖先节点的高度,并检查是否违反了平衡条件。如果发现某个祖先节点的平衡因子超过1,则进行相应的旋转操作来恢复平衡。
删除元素时,先按照二叉搜索树的规则找到待删除的节点,并进行删除操作。然后,从删除位置向上回溯,更新每个祖先节点的高度,并检查是否违反了平衡条件。如果发现某个祖先节点的平衡因子超过1,则进行相应的旋转操作来恢复平衡。
AVL树的自平衡性保证了查找、插入和删除等操作的时间复杂度都能保持在O(log n)级别,使其成为一种高效的数据结构。然而,AVL树相对于其他平衡二叉搜索树(如红黑树)来说,需要更多的旋转操作,因此在频繁插入和删除操作的场景下,可能会导致性能的略微下降。
AVL树模拟实现
insert插入
左旋
左旋前提条件:
parent ->bf = 2cur->bf = 1
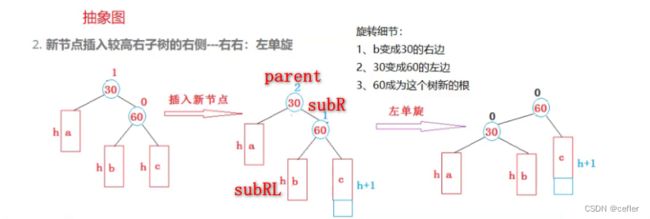
1.让parent->right = subRL;subR->left = parent;
2.此时还要更新根节点、parent的parent、subRL的parent(这个需要考虑subRL是否为空)
3.更新subR的parent,此时要考虑parent是否为根节点或非根节点两种情况。前者直接root = subR,subR->parent = nullptr,若为后者,则要另外讨论。
代码如下:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//1.让parent->right = subRL;subR->left = parent;
parent->_right = subRL;
subR->_left = parent;
//2.此时还要更新根节点、parent的parent、subRL的parent(**这个需要考虑subRL是否为空**)
Node* parentParent = parent->_parent;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
//更新subR的parent,此时要考虑parent是否为根节点或非根节点两种情况
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)//如果parent是parentParent的左节点,则作为新的"parent"的subR就要是parentParent的左节点,其parent为parentParent
{
parentParent->_left = subR;
subR->_parent = parentParent;
}
else
{
parentParent->_right = subR;
subR->_parent = parentParent;
}
}
parent->_bf = subR->_bf = 0;
}
右旋
右旋前提条件:
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//1.让parent->left = subLR;subL->right = parent;
parent->_left = subLR;
subL->_right = parent;
//2.此时还要更新根节点、parent的parent、subLR的parent(**这个需要考虑subRL是否为空**)
Node* parentParent = parent->_parent;
parent->_parent = subL;
if (subLR)
subLR->_parent = parent;
//3.更新subL的parent,此时要考虑parent是否为根节点或非根节点两种情况
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)//如果parent是parentParent的左节点,则作为新的"parent"的subR就要是parentParent的左节点,其parent为parentParent
{
parentParent->_left = subL;
subL->_parent = parentParent;
}
else
{
parentParent->_right = subL;
subL->_parent = parentParent;
}
}
parent->_bf = subL->_bf = 0;
}
双旋:先右单旋再左单旋
为什么要双旋转,是因为有单单左旋或右旋解决不了的情况:
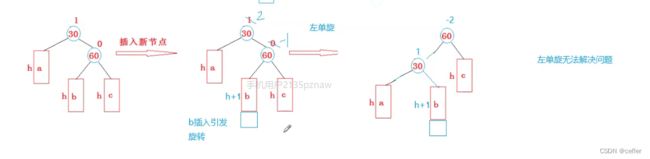
如上情况就左单旋无法解决问题
我们现在将上述的情况中的b子树再细分讨论

- a,d:高度为h(h>=0)
- b.c:高度为h-1,b,c可能为空树(h>=1)
但无论是哪种情况,都遵循一样的旋转步骤:
1.90为旋转点进行右旋
2.30为旋转点进行左旋
所以大致流程图可以表示为:

先右单旋再左单旋前提条件:
parent->_bf == 2cur->_bf == -1
所以大致步骤如下:
1.先对parent进行右旋
2.再对parent->right左旋
3.对parent、subR、subRL的bf进行更新
代码如下:
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
//先对parent进行右旋,再对parent->right左旋
RotateR(parent);
RotateL(parent->_left);
//对**parent**、**subR**、**subRL**的bf进行更新
//这里要考虑三种插入情况
if (bf == 0)
{
// subRL自己就是新增
subR->_bf = subRL->_bf = parent->_bf = 0;
}
else if (bf == -1)
{
//subRL左子树新增
subR->_bf = 1;
subRL->_bf = parent->_bf = 0;
}
else if (bf == 1)
{
//subRL右子树新增
parent->_bf = -1;
subRL->_bf = subR->_bf = 0;
}
else
{
assert(false);
}
}
双旋:先左单旋后右旋转
先左单旋后右旋转前提条件:
parent->bf = -2subL->bf = 1
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
//更新平衡因子
if (bf == 0)
{
parent->_bf = subL->_bf = subLR->_bf = 0;
}
else if (bf == 1)
{
subL->_bf = -1;
subLR->_bf = parent->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subLR->_bf = subL->_bf = 0;
}
else
{
assert(false);
}
}
判断是否为平衡树
bool IsBalance()
{
return _IsBalance(_root);
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
return true;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
if (rightHeight - leftHeight != root->_bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
AVLTree.h
#pragma once
#include 如上便是本期的所有内容了,如果喜欢并觉得有帮助的话,希望可以博个点赞+收藏+关注❤️ ,学海无涯苦作舟,愿与君一起共勉成长