红黑树
欢迎来到Cefler的博客
博客主页:那个传说中的man的主页
个人专栏:题目解析
推荐文章:题目大解析(3)
目录
- 红黑树概念与性质
- 红黑树插入
- ❤️RBTree.h
- map 和 set封装
-
- MyMap.h
- MySet.h
- RBTreePro.h
- map和set封装增加const迭代器,解决set能修改和map的first能修改问题
-
- MyMap.h
- MySet.h
- RBTreePro.h
红黑树概念与性质
概念 概念 概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍,因而是接近平衡的。
性质 性质 性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的 ✨
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 ✨
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
ps:空节点是为了更好的判别路径
判断红黑树思维逻辑顺序
1.根节点必须为黑,红不接红
2.所有路径上黑点数是否相同
3.最长路径有没有大于两倍最小路径
红黑树插入
若一开始红黑树为空,则第一次插入的节点必须为black。
若红黑树不为空,每次新插入节点,节点颜色初始默认为Red
- 如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整
- 但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论
情况讨论 情况讨论 情况讨论
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
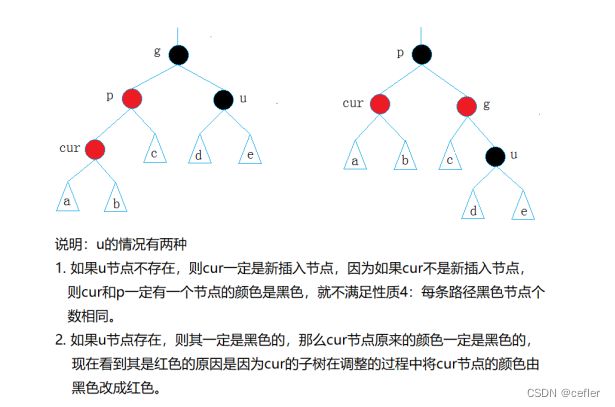
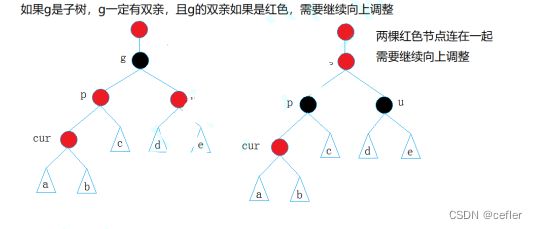
一、情况1: cur为红,p为红,g为黑,u存在且为红
解决方法:将p,u改为黑,g改为红,g当成cur,若g不为根节点继续向上调整,否则g改为黑

二、情况2: cur为红,p为红,g为黑,u不存在/u存在且为黑
- p为g的左孩子,cur为p的左孩子,则对g进行右单旋转
- p为g的右孩子,cur为p的右孩子,则对g进行左单旋转
最后:p改为black,g改为Red;
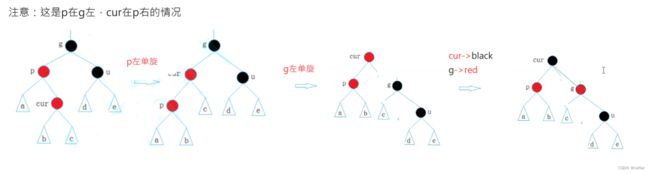
三、情况3: cur为红,p为红,g为黑,u不存在/u存在且为黑
与情况2略有不同的就是
❤️RBTree.h
#pragma once
#includemap 和 set封装
MyMap.h
#pragma once
#include"RBTreePro.h"
namespace space
{
template <class K,class V>
class map
{
public:
struct MapkeyofT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
//begin ,end,insert
// 对类模板取内嵌类型,加typename告诉编译器这里是类型;那不然编译器不知道内嵌类型到底是变量还是类型
typedef typename RBTree<K, pair<K, V>, MapkeyofT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _t.Insert(kv);
}
private:
RBTree<K, pair<K, V>, MapkeyofT> _t;
};
}
内嵌类型 内嵌类型 内嵌类型
在C++中,内嵌类型通常是指将一个类型定义为另一个类或结构体的成员类型。通过在类或结构体内部定义其他类型,可以将其视为该类或结构体的一部分,并使用作用域运算符(::)来访问这些内嵌类型。
因此,在C++中,内嵌类型提供了一种将复杂数据结构组织在一起的方式,使得代码更加清晰和模块化。
MySet.h
#pragma once
#include "MySet.h"
namespace space
{
template <class K>
class set
{
public:
struct SetkeyofT
{
const K& operator()(const K& key)
{
return key;
}
};
typedef typename RBTree<K, K, SetkeyofT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
private:
RBTree<K, K, SetkeyofT> _t;
};
}
RBTreePro.h
#pragma once
#include _t;
// map->RBTree, MapKeyOfT> _t;
template <class K, class T,class keyofT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef _TreeIterator<T> iterator;
iterator begin()
{
//找最左非空子树即可
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);//_root->parent就是nullptr
}
pair<iterator,bool> Insert(const T& data)
{
if (_root == nullptr)//第一次插入
{
_root = new Node(data);//那就创建一个新节点
_root->_col = BLACK;//根节点必须为黑
return make_pair(iterator(_root), true);
}
//如果不是第一次插入,则需要找到空节点插入
Node* parent = nullptr;
Node* cur = _root;
keyofT kot;
while (cur)
{
if (kot(cur->_data)>kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return make_pair(iterator(cur),false);
}
}
//找到后,创建新节点以供插入
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;//新节点必须为红
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}
//现在要对这个新插入的节点进行颜色检查和调整
//若父节点为空(即检查到了根)或者父节点此时为黑色,则不用调整;否则进行调整
//调整则按照我们的三情况
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
//这里我们必须要先分析p到底在g的左边还是右边
if (parent == grandfather->_left)//p在左边
{
// g
// p u
//cur
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED && parent->_col == RED && grandfather->_col == BLACK)//情况1:其实这里parent->_col == RED && grandfather->_col == BLACK就不用写了
//因为如果不符合这些要求,就不是红黑树前提了
{
//将p,u改为黑,g改为红,g当成cur,若g不为根节点继续向上调整,否则g改为黑
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;//继续向上调整
}
else
{
//情况2,3
if (cur == parent->_left)//情况2
{
// g
// p u
//cur
//p为g的左孩子,cur为p的左孩子,则进行右单旋转;最后:p->black,g->red
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况3
{
// g
// p u
// cur
//p为g的左孩子,cur为p的右孩子:则针对p做左单旋转,再对g做左单旋转;最后:cur改为black, g改为Red
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;//这时不用再向上调整直接退出即可(其实不break,此时的parent也已经不满足条件了)
}
}
else//p在右边
{
// g
// u p
// cur
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)//情况1
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;//继续向上调整
parent = cur->_parent;//继续向上调整
}
else
{
//情况2,3
if (cur == parent->_right)//情况2
{
// g
// u p
// cur
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况3
{
// g
// u p
// cur
//p为g的左孩子,cur为p的左孩子:则针对p做右单旋转,再对g做左单旋转;最后:cur改为black, g改为Red
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;//这一操作很妙,因为到最后肯定到了根节点,而根节点一定得为黑,所以直接将根节点改为黑就行
return make_pair(iterator(newnode),true);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
subR->_left = parent;
Node* parentParent = parent->_parent;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
bool Check(Node* root, int blacknum, const int refVal)
{
if (root == nullptr)//遇到空了此时对比一下这个路径的黑色节点数是否与refVal相等
{
//cout << balcknum << endl;
if (blacknum != refVal)
{
cout << "存在黑色节点数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "有连续的红色节点" << endl;
return false;
}
if (root->_col == BLACK)
{
++blacknum;
}
return Check(root->_left, blacknum, refVal)
&& Check(root->_right, blacknum, refVal);
}
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col == RED)
return false;
//参考值
int refVal = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refVal;
}
cur = cur->_left;
}
int blacknum = 0;
return Check(_root, blacknum, refVal);
}
private:
Node* _root = nullptr;
};
map和set封装增加const迭代器,解决set能修改和map的first能修改问题
MyMap.h
#pragma once
#include"RBTreePro.h"
namespace space
{
template <class K,class V>
class map
{
public:
struct MapkeyofT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
//begin ,end,insert
// 对类模板取内嵌类型,加typename告诉编译器这里是类型;那不然编译器不知道内嵌类型到底是变量还是类型
typedef typename RBTree<K, pair<const K, V>, MapkeyofT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapkeyofT>::const_iterator const_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<const K, V>, MapkeyofT> _t;//const修饰K,这样就可以保证K不能被修改,但V可以被修改
};
}
MySet.h
#pragma once
#include "MySet.h"
namespace space
{
template <class K>
class set
{
public:
struct SetkeyofT
{
const K& operator()(const K& key)
{
return key;
}
};
//两个迭代器本质上都是const_iterator
typedef typename RBTree<K, K, SetkeyofT>::const_iterator iterator;
typedef typename RBTree<K, K, SetkeyofT>::const_iterator const_iterator;
iterator begin()const
{
return _t.begin();
}
iterator end()const
{
return _t.end();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
private:
RBTree<K, K, SetkeyofT> _t;
};
}
RBTreePro.h
#pragma once
#include _t;
// map->RBTree, MapKeyOfT> _t;
template <class K, class T,class keyofT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef _TreeIterator<T,T&,T*> iterator;
typedef _TreeIterator<T, const T&, const T*> const_iterator;
iterator begin()
{
//找最左非空子树即可
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);//_root->parent就是nullptr
}
//const迭代器
const_iterator begin()const
{
//找最左非空子树即可
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return const_iterator(cur);
}
const_iterator end()const
{
return const_iterator(nullptr);//_root->parent就是nullptr
}
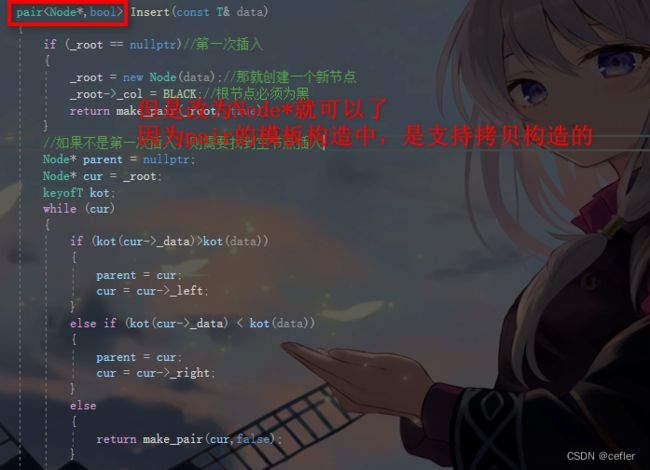
pair<Node*,bool> Insert(const T& data)
{
if (_root == nullptr)//第一次插入
{
_root = new Node(data);//那就创建一个新节点
_root->_col = BLACK;//根节点必须为黑
return make_pair(_root, true);
}
//如果不是第一次插入,则需要找到空节点插入
Node* parent = nullptr;
Node* cur = _root;
keyofT kot;
while (cur)
{
if (kot(cur->_data)>kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return make_pair(cur,false);
}
}
//找到后,创建新节点以供插入
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;//新节点必须为红
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}
//现在要对这个新插入的节点进行颜色检查和调整
//若父节点为空(即检查到了根)或者父节点此时为黑色,则不用调整;否则进行调整
//调整则按照我们的三情况
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
//这里我们必须要先分析p到底在g的左边还是右边
if (parent == grandfather->_left)//p在左边
{
// g
// p u
//cur
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED && parent->_col == RED && grandfather->_col == BLACK)//情况1:其实这里parent->_col == RED && grandfather->_col == BLACK就不用写了
//因为如果不符合这些要求,就不是红黑树前提了
{
//将p,u改为黑,g改为红,g当成cur,若g不为根节点继续向上调整,否则g改为黑
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;//继续向上调整
}
else
{
//情况2,3
if (cur == parent->_left)//情况2
{
// g
// p u
//cur
//p为g的左孩子,cur为p的左孩子,则进行右单旋转;最后:p->black,g->red
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况3
{
// g
// p u
// cur
//p为g的左孩子,cur为p的右孩子:则针对p做左单旋转,再对g做左单旋转;最后:cur改为black, g改为Red
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;//这时不用再向上调整直接退出即可(其实不break,此时的parent也已经不满足条件了)
}
}
else//p在右边
{
// g
// u p
// cur
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)//情况1
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;//继续向上调整
parent = cur->_parent;//继续向上调整
}
else
{
//情况2,3
if (cur == parent->_right)//情况2
{
// g
// u p
// cur
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况3
{
// g
// u p
// cur
//p为g的左孩子,cur为p的左孩子:则针对p做右单旋转,再对g做左单旋转;最后:cur改为black, g改为Red
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;//这一操作很妙,因为到最后肯定到了根节点,而根节点一定得为黑,所以直接将根节点改为黑就行
return make_pair(newnode,true);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
subR->_left = parent;
Node* parentParent = parent->_parent;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
bool Check(Node* root, int blacknum, const int refVal)
{
if (root == nullptr)//遇到空了此时对比一下这个路径的黑色节点数是否与refVal相等
{
//cout << balcknum << endl;
if (blacknum != refVal)
{
cout << "存在黑色节点数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "有连续的红色节点" << endl;
return false;
}
if (root->_col == BLACK)
{
++blacknum;
}
return Check(root->_left, blacknum, refVal)
&& Check(root->_right, blacknum, refVal);
}
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col == RED)
return false;
//参考值
int refVal = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refVal;
}
cur = cur->_left;
}
int blacknum = 0;
return Check(_root, blacknum, refVal);
}
private:
Node* _root = nullptr;
};
如上便是本期的所有内容了,如果喜欢并觉得有帮助的话,希望可以博个点赞+收藏+关注❤️ ,学海无涯苦作舟,愿与君一起共勉成长