立体视觉四十二章经第03章:SIFT特征提取原理及加速计算
本章目录
- SIFT算法来源
-
- 基于LOG的特征检测
-
- 构建尺度空间
- 对平滑后的图像进行归一化拉普拉斯变换
- 求归一化LOG极值并进行非极大值抑制
- 基于DOG的特征检测
- SIFT算法流程
-
- 构建尺度空间
-
- 高斯滤波器
- 一维离散高斯卷积核权重计算(已知平滑因子)
- 一维离散高斯卷积核权重计算(已知高斯核尺寸)
- 线性采样(硬件加速)
- 尺度空间构造详细流程
- 关键点粗定位
- 关键点精定位
- 消除边缘响应
- 方向分配
- 关键点描述子
- 参考文献
SIFT算法来源
特征提取有多中方法,本章主要讲解基于差分高斯(DOG)的sift特征提取方法,在此之前首先简单介绍下sift 的前身,基于高斯拉普拉斯(LOG)的特征提取方法。
基于LOG的特征检测
Lindeberg(1993)提出Laplacian of Gaussian(LoG)函数的极值点对应着特征点。基于LOG的特征检测主要分三步:
构建尺度空间

图 1 、构建原始图像尺度空间 图1、构建原始图像尺度空间 图1、构建原始图像尺度空间
对图像进行平滑,去除噪声点影像:
L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) L(x,y,\sigma)=G(x,y,\sigma)*I(x,y) L(x,y,σ)=G(x,y,σ)∗I(x,y)
其中*是 x , y x,y x,y上的卷积操作且:
G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 G(x,y,\sigma)=\dfrac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2} G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
σ ∈ { σ 0 , k σ 0 , k 2 σ 0 , . . . , 2 σ 0 , 2 k σ 0 , 2 k 2 σ 0 , . . . , 4 σ 0 , 4 k σ 0 , 4 k 2 σ 0 , . . . , 8 σ 0 , 8 k σ 0 } \sigma\in\{\sigma_0,k\sigma_0,k^2\sigma_0,...,2\sigma_0,2k\sigma_0,2k^2\sigma_0,...,4\sigma_0,4k\sigma_0,4k^2\sigma_0,...,8\sigma_0,8k\sigma_0\} σ∈{σ0,kσ0,k2σ0,...,2σ0,2kσ0,2k2σ0,...,4σ0,4kσ0,4k2σ0,...,8σ0,8kσ0}
令 k = 1 / 3 k=1/3 k=1/3,则:
σ ∈ { σ 0 , 2 1 / 3 σ 0 , 2 2 / 3 σ 0 , 2 σ 0 , 2 4 / 3 σ 0 , 2 5 / 3 σ 0 , 4 σ 0 , 2 7 / 3 σ 0 , 2 8 / 3 σ 0 , 8 σ 0 , 2 10 / 3 σ 0 } \sigma\in\{\sigma_0,2^{1/3}\sigma_0,2^{2/3}\sigma_0,2\sigma_0,2^{4/3}\sigma_0,2^{5/3}\sigma_0,4\sigma_0,2^{7/3}\sigma_0,2^{8/3}\sigma_0,8\sigma_0,2^{10/3}\sigma_0\} σ∈{σ0,21/3σ0,22/3σ0,2σ0,24/3σ0,25/3σ0,4σ0,27/3σ0,28/3σ0,8σ0,210/3σ0}
对平滑后的图像进行归一化拉普拉斯变换
∇ n o r m 2 L ( x , y , σ ) = σ 2 { ∂ 2 L ( x , y , σ ) ∂ x 2 + ∂ 2 L ( x , y , σ ) ∂ y 2 } \nabla_{norm}^{2}L(x,y,\sigma)=\sigma^2\left\{ \begin{aligned}\frac {\partial^2L(x,y,\sigma) } {\partial x^2 }+\frac{\partial^2 L(x,y,\sigma)}{\partial y^2}\end{aligned} \right\} ∇norm2L(x,y,σ)=σ2{∂x2∂2L(x,y,σ)+∂y2∂2L(x,y,σ)}
求归一化LOG极值并进行非极大值抑制
同时在位置 ( x , y ) (x,y) (x,y)和尺度 ( 2 1 / 3 σ 0 , . . . , 8 σ 0 ) (2^{1/3}\sigma_0,...,8\sigma_0) (21/3σ0,...,8σ0)空间上求LOG极值并进行非极大值抑制。
基于DOG的特征检测
基于LOG的特征提取精度高,但是太过耗时,Lowe(2004)提出LOG近似等价于相邻尺度的高斯差分(DOG)。
由heat diffusion方程:
∂ G ∂ σ = σ ∇ 2 G \frac{\partial G}{\partial \sigma}=\sigma\nabla^2G ∂σ∂G=σ∇2G
知使用 k σ k\sigma kσ和 σ \sigma σ附近的尺度之差做有限差分求 ∂ G ∂ σ \frac{\partial G} {\partial \sigma} ∂σ∂G的近似,进而计算出 ∇ 2 G \nabla^2G ∇2G:
σ ∇ 2 G = ∂ G ∂ σ ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \sigma\nabla^2G=\frac{\partial G}{\partial \sigma} \approx \frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma} σ∇2G=∂σ∂G≈kσ−σG(x,y,kσ)−G(x,y,σ)
因此:
G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G G(x,y,k\sigma)-G(x,y,\sigma) \approx (k-1)\sigma^2\nabla^2G G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G
约等号两边同时对图像做卷积得:
D ( x , y , σ ) ≈ ( k − 1 ) ∇ n o r m 2 L ( x , y , σ ) D(x,y,\sigma) \approx (k-1)\nabla_{norm}^{2}L(x,y,\sigma) D(x,y,σ)≈(k−1)∇norm2L(x,y,σ)
由此可见LoG近似等价于相邻尺度的高斯差分(DoG),接下来详细介绍 sift 特征提取的主要流程。
SIFT算法流程
计算的第一阶段是在所有尺度和图像位置上进行搜索。该算法利用高斯差函数来识别具有尺度和方向不变性的潜在兴趣点。
构建尺度空间
图 2 、高斯尺度空间构建示意图,注意图示平滑因子为相对于原始图像的 图2、高斯尺度空间构建示意图,注意图示平滑因子为相对于原始图像的 图2、高斯尺度空间构建示意图,注意图示平滑因子为相对于原始图像的
模糊系数,实际操作中,随着输入图像分辨率的改变,该值也会改变。 模糊系数, 实际操作中,随着输入图像分辨率的改变,该值也会改变。 模糊系数,实际操作中,随着输入图像分辨率的改变,该值也会改变。
为了保证高斯模糊的连续性,有效差分也需要保持模糊连续性,所以 Octave1 的最后一个有效高斯差分
L ( x , y , k S + 1 σ ) − L ( x , y , k s σ ) L(x,y,k^{S+1}\sigma)-L(x,y,k^s\sigma) L(x,y,kS+1σ)−L(x,y,ksσ) 与 Octave2 的第一个有效高斯差分 L ( x , y , 2 k 2 σ ) − L ( x , y , 2 k σ ) L(x,y,2k^2\sigma)-L(x,y,2k\sigma) L(x,y,2k2σ)−L(x,y,2kσ) 连续,因此:
k S + 1 σ = 2 k σ k^{S+1}\sigma=2k\sigma kS+1σ=2kσ
解得:
k = 2 1 S k=2^{\frac{1}{S}} k=2S1
实际操作中,在构造尺度空间时,每到下一个 octave 图像就下采样一次,而作用尺度与上一个 octave 的同一个位置相等,与图像不下采样且用 2 倍尺度相比,这种方式精度没有什么损失,计算量却大大减小。
高斯滤波器
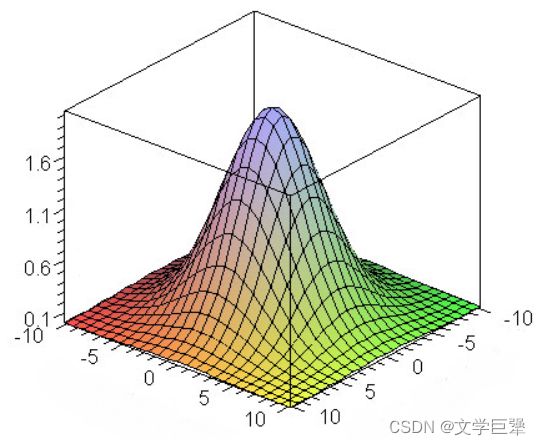
图 3 、二维高斯函数的图形表示 图3、二维高斯函数的图形表示 图3、二维高斯函数的图形表示
图像空间高斯滤波器是一个 N ∗ N N*N N∗N卷积滤波器,它基于高斯函数对其占用空间内的像素进行加权:
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 = 1 2 π σ 2 e − x 2 2 σ 2 ∗ 1 2 π σ 2 e − y 2 2 σ 2 = G ( x ) ∗ G ( y ) G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}*\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}=G(x)*G(y) G(x,y)=2πσ21e−2σ2x2+y2=2πσ21e−2σ2x2∗2πσ21e−2σ2y2=G(x)∗G(y)
由上述公式可知,作用在图像上的二维高斯滤波器可以拆解成两个一维高斯滤波器,接下来介绍如何生成一维离散高斯滤波器的权重。一维离散高斯滤波器权重计算有两种方法,一种是已知平滑因子 σ \sigma σ 不知道高斯核尺寸,另外一种是已知高斯核尺寸但是不知道平滑因子 σ \sigma σ,下面逐一介绍。
一维离散高斯卷积核权重计算(已知平滑因子)
已知平滑因子,如何确定作用于图像上的高斯卷积核,假设平滑因子为 σ \sigma σ,则:
高斯函数:
G ( x ) = 1 2 π σ 2 e − x 2 2 σ 2 G(x) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2}{2\sigma^2}} G(x)=2πσ21e−2σ2x2
高斯核半径:
k e r n e l S i z e = ⌈ 4 ∗ σ ⌉ + 1 kernelSize = \lceil 4*\sigma \rceil + 1 kernelSize=⌈4∗σ⌉+1
每个位置的权重:
w i = 1 2 π σ 2 e − i 2 2 σ 2 , i / i n [ 0 , . . . k e r n e l S i z e − 1 ] w_i = \frac{1}{2\pi\sigma^2}e^{-\frac{i^2}{2\sigma^2}} , i/in[0,...kernelSize-1] wi=2πσ21e−2σ2i2,i/in[0,...kernelSize−1]
权重和:
s u m w = w 0 + 2 ∑ w i , i ∈ [ 1 , . . . k e r n e l S i z e − 1 ] sum_w = w_0 + 2\sum{w_i} ,i\in[1,...kernelSize-1] sumw=w0+2∑wi,i∈[1,...kernelSize−1]
归一化后的权重:
w i = w i s u m w w_i=\frac{w_i}{sum_w} wi=sumwwi
一维离散高斯卷积核权重计算(已知高斯核尺寸)
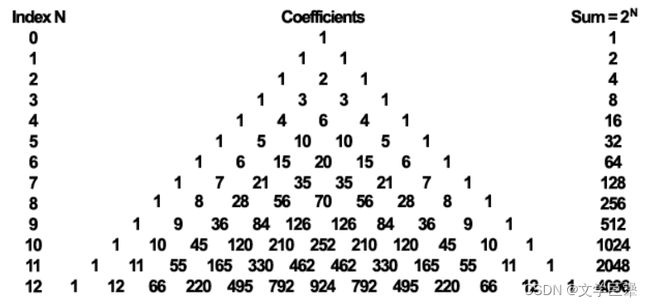
图 4 、帕斯卡三角形展示了可用于计算核权重的二项式系数 图4、帕斯卡三角形展示了可用于计算核权重的二项式系数 图4、帕斯卡三角形展示了可用于计算核权重的二项式系数
滤波器怎么计算每一个像素所占的权重。最显而易见的方式是为不同坐标分布计算高斯函数的值来确定卷积核权重。虽然这是很通用的方法,但有一种更方便的计算权重的方法:二项式系数。为什么能怎么做呢?因为高斯函数其实是正态分布函数,而正态分布的离散形式就是采用二项式系数做加权的二项式分布。
为了实现 9 x 1 水平滤波器和 1 x 9 垂直滤波器,我们将用到上图帕斯卡三角形的最后一行来计算权重。你可能会问,为什么不用 index 为 8 的行(它刚好有 9 个数字)?这是因为在典型的32位颜色缓冲上最边上的系数对最终结果没有任何的影响,而第二外层的系数对最终图像几乎没有影响。
有了必要的系数后,计算线性插值需要的权重就很简单了。只需将每个系数除以系数的总和(在这里是4096),当然为了纠正消去最外层四个系数的影响,应该将总和减到4070,否则图片在运用几次滤波器后就会变暗许多。
最终 9 x 1 水平滤波器系数为:
0.2270270270 , 0.1945945946 , 0.1216216216 , 0.0540540541 , 0.0162162162 , 0.0540540541 , 0.1216216216 , 0.1945945946 , 0.2270270270 0.2270270270, 0.1945945946, 0.1216216216, 0.0540540541, 0.0162162162,0.0540540541, 0.1216216216,0.1945945946,0.2270270270 0.2270270270,0.1945945946,0.1216216216,0.0540540541,0.0162162162,0.0540540541,0.1216216216,0.1945945946,0.2270270270
线性采样(硬件加速)
到此为止,我们假设了必须要做一次贴图读取来获得一个像素的信息,意味着 9 个像素需要 9 次贴图读取。尽管这对于在 CPU 上的实现来说是成立的,但在 GPU 上却不总是这样。这是因为在 GPU 上可以随意地使用双线性插值(bilinear sampling)而没有什么额外的负担。这意味着如果不在纹素中心读取贴图,就可以得到多个像素的信息。既然已经利用了高斯函数的可分离性,实际上是在1D下工作,双线性插值会提供2个像素的信息。每个像素对最终颜色的贡献量由使用的坐标决定。
通过正确地调整贴图读取的坐标偏移,可以仅通过一次贴图读取得到两个像素或纹素的准确信息。这意味着为了实现一个 9 x 1 或 1 x 9 的高斯滤波器只需要 5 次贴图读取。总的来说,实现 N x 1 或 1 x N 的滤波器需要 [N/2] 次贴图读取。
使用一个单独的纹理获取来获取关于两个texel的信息,我们必须通过两个 t e x e l texel texel 对应的权重之和来权衡检索到的颜色值。现在我们知道了我们的权重,我们只需要正确地计算纹理坐标偏移。
在合并两个 t e x e l texel texel 时,我们必须调整坐标,使确定的坐标到 t e x e l 1 texel_1 texel1 中心的距离应该等于 t e x e l 2 texel_2 texel2 的权重除以两个权重的总和,反之亦然。最终得到以下公式来确定我们的线性采样高斯模糊滤波器的权重和偏移量:
w e i g h t ( t 1 , t 2 ) = w e i g h t ( t 1 ) + w e i g h t ( t 2 ) weight(t_1,t_2)=weight(t_1)+weight(t_2) weight(t1,t2)=weight(t1)+weight(t2)
o f f s e t ( t 1 , t 2 ) = o f f s e t ( t 1 ) ⋅ w e i g h t ( t 1 ) + o f f s e t ( t 2 ) ⋅ w e i g h t ( t 2 ) w e i g h t ( t 1 , t 2 ) offset(t_1,t_2)=\frac{offset(t_1)\cdot weight(t_1)+offset(t_2)\cdot weight(t_2)}{weight(t_1,t_2)} offset(t1,t2)=weight(t1,t2)offset(t1)⋅weight(t1)+offset(t2)⋅weight(t2)
尺度空间构造详细流程
1、构造图像金字塔
假设 ocatave 数目为 num_octave,对图像进行 num_octave - 1 次二分之一降采样并保留每次降采样之前的数据。最终得到 num_octave 张不同分辨率的图像。
2、构造高斯卷积核
对于第一个 octave 中的第 i 个 scale,相对于原始图像作用于其上的尺度为 k i σ k^i\sigma kiσ 假设有效差分为 S = 3,则相对于原始图像第一个 octave 中的尺度分别为 σ , 2 1 3 σ , 2 2 3 σ , 2 3 3 σ , 2 4 3 σ , 2 5 3 σ \sigma,2^{\frac{1}{3}}\sigma,2^{\frac{2}{3}}\sigma,2^{\frac{3}{3}}\sigma,2^{\frac{4}{3}}\sigma,2^{\frac{5}{3}}\sigma σ,231σ,232σ,233σ,234σ,235σ。假设 σ = 1.6 \sigma=1.6 σ=1.6,图像初始平滑因子为 0.5,则 octave 中每个层还需要作用的平滑因子以及高斯核半径为:
第零层: σ 0 = ( 2 0 3 ∗ 1.6 ) 2 − 0. 5 2 = 1.51987 , k e r n e l 0 \sigma_0=\sqrt{(2^{\frac{0}{3}}*1.6)^2-0.5^2}=1.51987,kernel_0 σ0=(230∗1.6)2−0.52=1.51987,kernel0_size = ⌈ 4 ∗ σ 0 ⌉ + 1 = 8 \lceil 4*\sigma_0 \rceil + 1 = 8 ⌈4∗σ0⌉+1=8
第一层: σ 1 = ( 2 1 3 ∗ 1.6 ) 2 − σ 0 2 = 1.22627 , k e r n e l 1 \sigma_1=\sqrt{(2^{\frac{1}{3}}*1.6)^2-\sigma_0^2}=1.22627,kernel_1 σ1=(231∗1.6)2−σ02=1.22627,kernel1_size = ⌈ 4 ∗ σ 1 ⌉ + 1 = 6 \lceil 4*\sigma_1 \rceil + 1 = 6 ⌈4∗σ1⌉+1=6
第二层: σ 2 = ( 2 2 3 ∗ 1.6 ) 2 − σ 1 2 = 1.54501 , k e r n e l 2 \sigma_2=\sqrt{(2^{\frac{2}{3}}*1.6)^2-\sigma_1^2}=1.54501,kernel_2 σ2=(232∗1.6)2−σ12=1.54501,kernel2_size = ⌈ 4 ∗ σ 2 ⌉ + 1 = 8 \lceil 4*\sigma_2 \rceil + 1 = 8 ⌈4∗σ2⌉+1=8
第三层: σ 3 = ( 2 3 3 ∗ 1.6 ) 2 − σ 2 2 = 1.94659 , k e r n e l 3 \sigma_3=\sqrt{(2^{\frac{3}{3}}*1.6)^2-\sigma_2^2}=1.94659,kernel_3 σ3=(233∗1.6)2−σ22=1.94659,kernel3_size = ⌈ 4 ∗ σ 3 ⌉ + 1 = 9 \lceil 4*\sigma_3 \rceil + 1 = 9 ⌈4∗σ3⌉+1=9
第四层: σ 4 = ( 2 4 3 ∗ 1.6 ) 2 − σ 3 2 = 2.45255 , k e r n e l 4 \sigma_4=\sqrt{(2^{\frac{4}{3}}*1.6)^2-\sigma_3^2}=2.45255,kernel_4 σ4=(234∗1.6)2−σ32=2.45255,kernel4_size = ⌈ 4 ∗ σ 4 ⌉ + 1 = 11 \lceil 4*\sigma_4 \rceil + 1 = 11 ⌈4∗σ4⌉+1=11
第五层: σ 5 = ( 2 5 3 ∗ 1.6 ) 2 − σ 4 2 = 3.09002 , k e r n e l 5 \sigma_5=\sqrt{(2^{\frac{5}{3}}*1.6)^2-\sigma_4^2}=3.09002,kernel_5 σ5=(235∗1.6)2−σ42=3.09002,kernel5_size = ⌈ 4 ∗ σ 5 ⌉ + 1 = 14 \lceil 4*\sigma_5 \rceil + 1 = 14 ⌈4∗σ5⌉+1=14
根据一维高斯函数构造每一层一维高斯核:
第零层:
k e r n e l D a t a [ i ] = 1 2 π σ 0 2 e − i 2 2 σ 0 2 , i ∈ 0...7 kernelData[i] = \frac{1}{2\pi{\sigma_0}^2}e^{-\frac{i^2}{2{\sigma_0}^2}},i\in{0...7} kernelData[i]=2πσ021e−2σ02i2,i∈0...7
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...7 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...7} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...7
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
第一层:
k e r n e l D a t a [ i ] = 1 2 π σ 1 2 e − i 2 2 σ 1 2 , i ∈ 0...5 kernelData[i] = \frac{1}{2\pi{\sigma_1}^2}e^{-\frac{i^2}{2{\sigma_1}^2}},i\in{0...5} kernelData[i]=2πσ121e−2σ12i2,i∈0...5
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...5 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...5} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...5
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
第二层:
k e r n e l D a t a [ i ] = 1 2 π σ 2 2 e − i 2 2 σ 2 2 , i ∈ 0...7 kernelData[i] = \frac{1}{2\pi{\sigma_2}^2}e^{-\frac{i^2}{2{\sigma_2}^2}},i\in{0...7} kernelData[i]=2πσ221e−2σ22i2,i∈0...7
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...7 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...7} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...7
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
第三层:
k e r n e l D a t a [ i ] = 1 2 π σ 3 2 e − i 2 2 σ 3 2 , i ∈ 0...8 kernelData[i] = \frac{1}{2\pi{\sigma_3}^2}e^{-\frac{i^2}{2{\sigma_3}^2}},i\in{0...8} kernelData[i]=2πσ321e−2σ32i2,i∈0...8
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...8 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...8} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...8
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
第四层:
k e r n e l D a t a [ i ] = 1 2 π σ 4 2 e − i 2 2 σ 4 2 , i ∈ 0...10 kernelData[i] = \frac{1}{2\pi{\sigma_4}^2}e^{-\frac{i^2}{2{\sigma_4}^2}},i\in{0...10} kernelData[i]=2πσ421e−2σ42i2,i∈0...10
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...10 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...10} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...10
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
第五层:
k e r n e l D a t a [ i ] = 1 2 π σ 5 2 e − i 2 2 σ 5 2 , i ∈ 0...13 kernelData[i] = \frac{1}{2\pi{\sigma_5}^2}e^{-\frac{i^2}{2{\sigma_5}^2}},i\in{0...13} kernelData[i]=2πσ521e−2σ52i2,i∈0...13
k e r n e l D a t a S u m = k e r n e l D a t a [ 0 ] + 2 ∑ k e r n e l D a t a [ i ] , i ∈ 1...13 kernelDataSum = kernelData[0] + 2\sum{kernelData[i]},i\in{1...13} kernelDataSum=kernelData[0]+2∑kernelData[i],i∈1...13
f i n a l K e r n e l D a t a [ i ] = k e r n e l D a t a [ i ] k e r n e l D a t a S u m finalKernelData[i] = \frac{kernelData[i]}{kernelDataSum} finalKernelData[i]=kernelDataSumkernelData[i]
3、构造线性采样高斯核(可选项 gpu 加速)
4、对图像金字塔做卷积操作
- 对图像先进行水平一维高斯平滑,再进行垂直一维高斯平滑。
- 同一个 octave 中当前尺度计算完成后,保存平滑后的图像,并拷贝一份作为下一个尺度的输入。
- 因为降采样的原因,所以每个 octave 中相同 scale 对应的高斯核是一样的。
关键点粗定位
图 5 、关键点粗定位 图5、关键点粗定位 图5、关键点粗定位
通过将一个像素(用X标记)与当前和相邻尺度(用圆圈标记)下的3x3区域内的26个相邻像素进行比较,检测高斯差分图像的极大值和极小值。
关键点精定位

图 6 、该图显示了关键点选择的各个阶段。 ( a ) 233 x 189 像素的原始图像。 图6、该图显示了关键点选择的各个阶段。(a) 233x189像素的原始图像。 图6、该图显示了关键点选择的各个阶段。(a)233x189像素的原始图像。
( b ) 初始 832 个关键点位于高斯差分函数的最大值和最小值处。关键点以 (b)初始832个关键点位于高斯差分函数的最大值和最小值处。关键点以 (b)初始832个关键点位于高斯差分函数的最大值和最小值处。关键点以
向量的形式显示,表示模、方向和位置。 ( c ) 在应用最低对比度阈值后, 向量的形式显示,表示模、方向和位置。(c)在应用最低对比度阈值后, 向量的形式显示,表示模、方向和位置。(c)在应用最低对比度阈值后,
仍保留 729 个关键点。 ( d ) 附加主曲率比阈值后的最后 536 个关键点。 仍保留729个关键点。(d)附加主曲率比阈值后的最后536个关键点。 仍保留729个关键点。(d)附加主曲率比阈值后的最后536个关键点。
尺度空间极值检测得到的点是像素级的,为了得到更高精度的亚像素级结果,还需要利用泰勒展开式进行精准检测确定关键点的位置和尺度。
D ( x ) = D + ∂ D T ∂ x x + 1 2 x T ∂ 2 D ∂ x 2 x D(x)=D+\frac {\partial D^T } {\partial x }x + \frac {1} {2}x^T\frac {\partial^2D } {\partial x^2 }x D(x)=D+∂x∂DTx+21xT∂x2∂2Dx
D是极值检测步骤中计算的粗关键点,x是相对D所对应点的偏移量。上面的函数对x求导并取0,计算得:
x ^ = − ∂ 2 D − 1 ∂ x 2 ∂ D ∂ x \hat{x}=-\frac {\partial^2D^{-1} } {\partial x^2 }\frac {\partial D } {\partial x} x^=−∂x2∂2D−1∂x∂D
D ( x ^ ) = D + 1 2 ∂ D T ∂ x x ^ D(\hat{x})=D+\frac {1} {2}\frac {\partial D^T} {\partial x}\hat{x} D(x^)=D+21∂x∂DTx^
丢弃所有 ∣ D ( x ^ ) ∣ |D(\hat{x})| ∣D(x^)∣值小于0.03的极值(与之前一样,我们假设图像像素值在[0,1]范围内)。
消除边缘响应
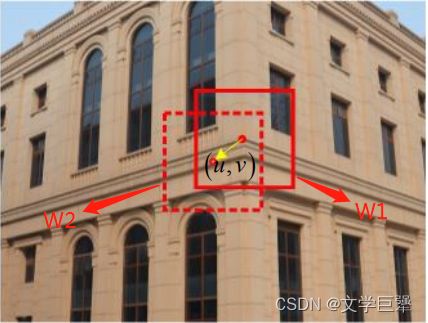
图 7 、计算点 ( u , v ) 处的 h a r r i r s 响应,实际是计算两个窗口内所有像素值的加权差异 图7、计算点(u,v)处的harrirs响应,实际是计算两个窗口内所有像素值的加权差异 图7、计算点(u,v)处的harrirs响应,实际是计算两个窗口内所有像素值的加权差异
以像素点 ( u , v ) (u,v) (u,v)为中心的窗口 W 1 W_1 W1经过平移 ( Δ u , Δ v ) (\Delta u,\Delta v) (Δu,Δv)得到窗口 W 2 W_2 W2,两个窗口的像素差异定义为:
E ( Δ u , Δ v ) = ∑ x , y w ( x , y ) [ I ( x + Δ u , y + Δ v ) − I ( x , y ) ] E(\Delta u,\Delta v)=\sum\limits_{x,y} w(x,y) [I(x+\Delta u,y+\Delta v) - I(x,y)] E(Δu,Δv)=x,y∑w(x,y)[I(x+Δu,y+Δv)−I(x,y)]
≈ ∑ x , y w ( x , y ) [ δ I δ x ( x , y ) Δ u + δ I δ y ( x , y ) Δ v ] 2 \approx\sum\limits_{x,y}w(x,y){[\frac{\delta I}{\delta x}(x,y)\Delta u+\frac{\delta I}{\delta y}(x,y)\Delta v]}^2 ≈x,y∑w(x,y)[δxδI(x,y)Δu+δyδI(x,y)Δv]2
= [ Δ u , Δ v ] H [ Δ u , Δ v ] T =[\Delta u,\Delta v]H{[\Delta u,\Delta v]}^T =[Δu,Δv]H[Δu,Δv]T
其中(x,y)为窗口W1内的像素点, ( x + Δ u , y + Δ v ) (x+\Delta u,y+\Delta v) (x+Δu,y+Δv)为窗口W2内像素点。 w ( x , y ) = e − ( x 2 + y 2 ) 2 σ 2 w(x,y)=\frac{e^{-(x^2+y^2)}}{2\sigma^2} w(x,y)=2σ2e−(x2+y2)为窗口内的高斯卷积核(和窗口同样大小)。
H = ∑ x , y w ( x , y ) ⋅ [ ( δ I δ x ( x , y ) ) 2 δ I δ x ( x , y ) ⋅ δ I δ y ( x , y ) δ I δ y ( x , y ) ⋅ δ I δ y ( x , y ) ( δ I δ y ( x , y ) ) 2 ] H=\sum\limits_{x,y}w(x,y)\cdot\left[\begin{matrix} (\frac{\delta I}{\delta x}(x,y))^2 & \frac{\delta I}{\delta x}(x,y)\cdot\frac{\delta I}{\delta y}(x,y) \\ \frac{\delta I}{\delta y}(x,y)\cdot\frac{\delta I}{\delta y}(x,y) & (\frac{\delta I}{\delta y}(x,y))^2 \end{matrix}\right] H=x,y∑w(x,y)⋅[(δxδI(x,y))2δyδI(x,y)⋅δyδI(x,y)δxδI(x,y)⋅δyδI(x,y)(δyδI(x,y))2]
计算关键点处的海森矩阵并过滤边缘处的关键点流程如下:
- 计算梯度图 X,Y
X = I ⨂ ( − 1 , 0 , 1 ) X=I\bigotimes(-1,0,1) X=I⨂(−1,0,1)
Y = I ⨂ ( − 1 , 0 , 1 ) T Y=I\bigotimes(-1,0,1)^T Y=I⨂(−1,0,1)T - 计算梯度图的卷积
A = X ⋅ X ⨂ w A=X\cdot X\bigotimes w A=X⋅X⨂w
B = Y ⋅ Y ⨂ w B=Y\cdot Y\bigotimes w B=Y⋅Y⨂w
C = X ⋅ Y ⨂ w C=X\cdot Y\bigotimes w C=X⋅Y⨂w
其中 ⋅ \cdot ⋅为梯度图矩阵对应位置相乘, w w w为5x5高斯卷积核(也可以为其他大小的高斯卷积核)
- 计算每个像素点 harris 响应值
设矩阵 H H H的特征值分别为 α , β \alpha,\beta α,β,则:
T r ( H ) = α + β = A ( u , v ) + B ( u , v ) Tr(H)=\alpha+\beta=A(u,v)+B(u,v) Tr(H)=α+β=A(u,v)+B(u,v)
D e t ( H ) = α β = A ( u , v ) B ( u , v ) − C 2 ( u , v ) Det(H)=\alpha\beta=A(u,v)B(u,v)-C^2(u,v) Det(H)=αβ=A(u,v)B(u,v)−C2(u,v)
像素点 ( u , v ) (u,v) (u,v)的harris的响应值(response)为:
R ( u , v ) = D e t ( H ) − k ⋅ T r 2 ( H ) R(u,v)=Det(H)-k\cdot {Tr}^2(H) R(u,v)=Det(H)−k⋅Tr2(H)
其中 k = 0.04 k=0.04 k=0.04(也可以为其他值),如果 R ( u , v ) > 0 R(u,v)>0 R(u,v)>0,则删除该关键点。
方向分配
图 8 、梯度直方图计算主方向 图8、梯度直方图计算主方向 图8、梯度直方图计算主方向
根据局部图像属性为每个关键点分配方向,关键点描述符相对于该方向表示,从而实现对图像旋转的不变性。
利用关键点的尺度选择最接近该尺度的高斯平滑图像 L L L,在平滑图像 L L L上计算使所有计算关键点周围8*8邻域内每个像素的梯度幅度 m ( x , y ) m(x, y) m(x,y)和方向 θ ( x , y ) \theta(x, y) θ(x,y)。
m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2 m(x,y)=\sqrt{{(L(x+1,y)-L(x-1,y))}^2+{(L(x,y+1)-L(x,y-1))}^2} m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2
θ ( x , y ) = t a n − 1 L ( x , y + 1 ) − L ( x , y − 1 ) L ( x + 1 , y ) − L ( x − 1 , y ) \theta(x,y)=tan^{-1}\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)} θ(x,y)=tan−1L(x+1,y)−L(x−1,y)L(x,y+1)−L(x,y−1)
利用关键点邻域内样像素点的梯度和方向构建方向直方图。直方图有36个 b i n bin bin,覆盖360度的方向范围。方差为 1.5 ∗ σ 1.5*\sigma 1.5∗σ的高斯模板作用于关键点邻域内的像素梯度,统计出每个方位的加权梯度和作为直方图的纵坐标。
直方图峰值对应的角度记为关键点的主方向。对于高于峰值80%以上的其他局部峰值对应的方向记为关键点的辅方向。
关键点描述子
前面的操作为每个关键点分配了一个图像位置、比例和方向。这些参数构成了一个可重复的局部二维坐标系,用于描述局部图像区域,因此提供了这些参数的不变性。下一步是计算局部图像区域的描述符,该描述符高度独特,但尽可能不受其余变化的影响,如照明或3D视点的变化。
图 9 、关键点邻域按主方向旋转 图9、关键点邻域按主方向旋转 图9、关键点邻域按主方向旋转
根据主方向对支持区域进行旋转,并通过双线性插值重构得到旋转后的关键点邻域(旋转前正方形领域平行于图像坐标系,旋转后的正方形领域与图像坐标系有夹角)。利用下面公式对图像归一化,去除光照影响。
I ′ = I − u s I^{'}=\frac{I-u}{s} I′=sI−u
图 10 、生成最终的描述子 图10、生成最终的描述子 图10、生成最终的描述子
将区域划分成4*4的block,统计每个block梯度方向直方图(高斯加权梯度作为系数),并将结果串联起来形成128维向量。
参考文献
1、Distinctive Image Features from Scale-Invariant Keypoints