图像几何变换C++实现--镜像，平移，旋转，错切，缩放

转载请注明出处。
文章地址：https://blog.csdn.net/duiwangxiaomi/article/details/109532590?spm=1001.2014.3001.5501

    贴一个理解仿射变换及其矩阵的网址。
    仿射变换

一.图像几何变换介绍

    图像的几何空间变换是图像处理中的最基础的算法，是指对原始图像按需要改变其大小、形状和位置的变化，原始图像与目标函数之间的坐标变换函数为线性函数。二维图像的基本几何变换主要包括镜像、平移、缩放、旋转、错切(偏移)等操作，上述变换又称为仿射变换，在冈萨雷斯的数字图像处理第三版的第二章就做了相关介绍，数字图像处理第三版下载地址。

    下面逐一介绍上述几种放射变换。

二.变换详解

    常见几种变换公式如下表所示

    在进行变换时，其中镜像、平移、缩放均以图像像素坐标系(图像左上顶点为坐标系原点)进行。
    对于旋转和错切一般以图像中心为原点，此时在操作中需要加上坐标系转换公式。图像坐标系和旋转坐标系如下图所示，

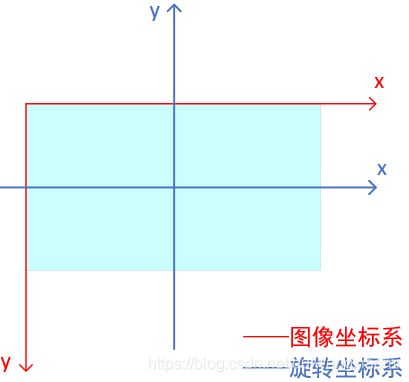
    旋转和错切变换分为3步，

1. 将图像坐标转换到旋转坐标系；
2. 根据上述表格公式进行旋转或错切变换；
3. 将旋转坐标系转换到图像坐标系；
   实际实现时可将三个矩阵合并进行计算，本文的实现即采用此种方法。

变换方式

1. 前向映射
   

2. 反向映射
   
       由于旋转、缩放、变形变换中会出现漏点、不规则点问题，如果用前向映射，会导致得到的图像中有很多黑点，对于这种情况，通常采用反向映射。
       反向映射需通过插值方法决定输出图像该位置的值，因此需要选择插值算法。通常有最近邻插值、双线性插值，双三次插值等，具体的差值方法、原理及优缺点自行百度吧，我们这里采用双线性插值。

三.C++实现

    实现功能：镜像、旋转、平移、缩放、错切、组合变换。利用了OpenCV的Mat，指针实现的后期有时间再补充。编程环境：VS2013+OpenCV2.4.13

#include 
#include 

using namespace std;
using namespace cv;

#define PI 3.1415927
#define MAX(a,b) (((a)>(b))?(a):(b))

// 单点双线性插值
// [输入]	ii--dst的行索引
//			jj--dst的列索引	
//			u_src--jj反向映射到src中对应的列索引
//			v_src--ii反向映射到src中对应的行索引
int Bilinear_interpolation_img(Mat src, Mat& dst, int ii, int jj, double u_src, double v_src)
{
	if (src.rows <= 0 || src.cols <= 0 || 
	(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	if (u_src >= 0 && u_src <= src.cols - 1 && v_src >= 0 && v_src <= src.rows - 1)
	{
		int x1 = int(u_src), x2 = (int)(u_src + 0.5), y1 = (int)v_src, y2 = (int)(v_src + 0.5);
		double pu = fabs(u_src - x1), pv = fabs(v_src - y2);
		if (src.channels() == 1)
		{
			dst.at<uchar>(ii, jj) = (1 - pv)*(1 - pu)*src.at<uchar>(y2, x1) + 
			(1 - pv)*pu*src.at<uchar>(y2, x2) +
			pv*(1 - pu)*src.at<uchar>(y1, x1) + pv*pu*src.at<uchar>(y1, x2);
		}
		else
		{
			dst.at<Vec3b>(ii, jj)[0] = (1 - pv)*(1 - pu)*src.at<Vec3b>(y2, x1)[0] + 
			(1 - pv)*pu*src.at<Vec3b>(y2, x2)[0] +
				pv*(1 - pu)*src.at<Vec3b>(y1, x1)[0] + 
				pv*pu*src.at<Vec3b>(y1, x2)[0];
			dst.at<Vec3b>(ii, jj)[1] = (1 - pv)*(1 - pu)*src.at<Vec3b>(y2, x1)[1] + 
			(1 - pv)*pu*src.at<Vec3b>(y2, x2)[1] +
				pv*(1 - pu)*src.at<Vec3b>(y1, x1)[1] + 
				pv*pu*src.at<Vec3b>(y1, x2)[1];
			dst.at<Vec3b>(ii, jj)[2] = (1 - pv)*(1 - pu)*src.at<Vec3b>(y2, x1)[2] + 
			(1 - pv)*pu*src.at<Vec3b>(y2, x2)[2] +
				pv*(1 - pu)*src.at<Vec3b>(y1, x1)[2] + 
				pv*pu*src.at<Vec3b>(y1, x2)[2];
		}

	}
	return 1;
}

//水平镜像、垂直镜像变换
// [输入]	way_mirror镜像方法：0水平镜像 1垂直镜像
int affine_mirrorImg(Mat src, Mat& dst, int way_mirror)
{
	if (src.rows <= 0 || src.cols <= 0 || 
		(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U){
		printf("输入图像有误!\n");
		return 0;
	}

	if (way_mirror != 0 && way_mirror != 1){
		printf("输入镜像方法不为1或0,way_mirror: %d!\n",way_mirror);
		return 0;
	}

	int dst_h = src.rows, dst_w = src.cols;//目标图像宽高 初始化为原图宽高
	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	Mat M_mirr = (Mat_<double>(3, 3) << -1, 0, 0, 0, 1, 0, 0, 0, 1);
	if (way_mirror){
		M_mirr.at<double>(0,0) = 1;
		M_mirr.at<double>(1, 1) = -1;
	}
	Mat M_corrToSrc = (Mat_<double>(3, 3) << 1, 0, src.cols, 0, 1, 0, 0, 0, 1);
	if (way_mirror){
		M_corrToSrc.at<double>(0, 2) = 0;
		M_corrToSrc.at<double>(1, 2) = src.rows;
	}
	Mat M_trans = M_corrToSrc*M_mirr;

	Mat M_trans_inv = M_trans.inv();
	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	if (src.channels() == 3)
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
	else
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);

	//反向映射
	for (ii = 0; ii < dst_h; ++ii)
	{
		for (jj = 0; jj < dst_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			// 边界问题
			if (u_src < 0) u_src = 0;
			if (v_src < 0) v_src = 0;
			if (u_src>src.cols - 1) u_src = src.cols - 1;
			if (v_src>src.rows - 1) v_src = src.rows - 1;

			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
		}
	}
	return 1;
}

// 图像旋转(绕图像中心) 逆时针旋转为正
// 可处理8位单通道或三通道图像
int affine_rotateImg(Mat src, Mat& dst, double Angle)
{
	if (src.rows <= 0 || src.cols <= 0 || 
	(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	double angle =0,cos_a=0,sin_a=0;//旋转角度
	int dst_h = src.rows, dst_w = src.cols;//目标图像宽高 初始化为原图宽高
	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	angle = Angle / 180 * CV_PI;
	cos_a = cos(angle);
	sin_a = sin(angle);
	dst_h = (int)(fabs(src.rows*cos_a) + fabs(src.cols*sin_a) + 0.5);
	dst_w = (int)(fabs(src.rows*sin_a) + fabs(src.cols*cos_a) + 0.5);

	if (src.channels()==3)
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
	}
	else
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
	}
	Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5*src.cols, 0, -1, 0.5*src.rows, 0, 0, 1);
	Mat M_rotate = (Mat_<double>(3, 3) << cos_a, -sin_a, 0, sin_a, cos_a, 0, 0, 0, 1);
	Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5*dst.cols, 0, -1, 0.5*dst.rows, 0,0,1);
	Mat M_trans = M_toPixel*M_rotate*M_toPhysics;
	Mat M_trans_inv = M_trans.inv();
	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	//反向映射
	for (ii = 0; ii < dst_h; ++ii)
	{
		for (jj = 0; jj < dst_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			//处理边界问题
			if (int(Angle) % 90 == 0)
			{
				if (u_src < 0) u_src = 0;
				if (v_src < 0) v_src = 0;
				if (u_src>src.cols - 1) u_src = src.cols - 1;
				if (v_src>src.rows - 1) v_src = src.rows - 1;
			}
			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
		}
	}

	return 1;
}

// 图像平移 在像素坐标系下进行 图像左顶点为原点，x轴为图像列，y轴为图像行
// tx： x方向(图像列)平移量,向右平移为正
// ty： y方向(图像行)平移量,向下平移为正
int affine_moveImg(Mat src, Mat& dst, double tx, double ty)
{
	if (src.rows <= 0 || src.cols <= 0 || 
	(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	int dst_h = src.rows, dst_w = src.cols;
	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	if (src.channels() == 3)
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
	}
	else
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
	}

	Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, tx, 0, 1, ty, 0, 0, 1);
	Mat M_trans_inv = M_toPhysics.inv();
	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	//反向映射
	for (ii = 0; ii < dst_h; ++ii)
	{
		for (jj = 0; jj < dst_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);

		}
	}

	return 1;
}

// 缩放 以图像左顶点为原点
// cx: 水平缩放尺度
// cy: 垂直缩放尺度
int affine_scalingImg(Mat src, Mat& dst, double cx, double cy)
{
	if (src.rows <= 0 || src.cols <= 0 || 
	(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	int dst_h = (int)(cy*src.rows+0.5), dst_w =(int)(cx* src.cols+0.5);
	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	if (src.channels() == 3)
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
	}
	else
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
	}

	Mat M_scale = (Mat_<double>(3, 3) << cx, 0, 0, 0, cy, 0, 0, 0, 1);
	Mat M_trans_inv = M_scale.inv();
	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	//反向映射
	for (ii = 0; ii < dst_h; ++ii)
	{
		for (jj = 0; jj < dst_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			// 边界问题
			if (u_src < 0) u_src = 0;
			if (v_src < 0) v_src = 0;
			if (u_src>src.cols - 1) u_src = src.cols - 1;
			if (v_src>src.rows - 1) v_src = src.rows - 1;

			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
		}
	}
	return 1;
}

// 错切变换 以图像中心为偏移中心
// [输入]	sx--水平错切系数
//			sy--垂直错切系数		
int affine_miscut(Mat src, Mat& dst, double sx, double sy)
{
	if (src.rows <= 0 || src.cols <= 0 || 
	(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	int dst_h = fabs(sy)*src.cols + src.rows, dst_w = fabs(sx)*src.rows + src.cols;
	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	if (src.channels() == 3)
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
	}
	else
	{
		dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
	}

	Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5*src.cols, 0, -1, 0.5*src.rows, 0, 0, 1);
	Mat M_rotate = (Mat_<double>(3, 3) << 1, sx, 0, sy, 1, 0, 0, 0, 1);
	Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5*dst.cols, 0, -1, 0.5*dst.rows, 0, 0, 1);
	Mat M_trans = M_toPixel*M_rotate*M_toPhysics;
	Mat M_trans_inv = M_trans.inv();
	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	//反向映射
	for (ii = 0; ii < dst_h; ++ii)
	{
		for (jj = 0; jj < dst_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
		}
	}

	return 1;
}

// 组合变换示例
// 缩放->旋转->错切(即偏移)
// [输入]	
int affine_srm_combImg(Mat src, Mat& dst, double cx, double cy, double Angle, double sx, double sy)
{
	if (src.rows <= 0 || src.cols <= 0 || 
		(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
	{
		printf("输入图像有误!\n");
		return 0;
	}

	double angle, cos_a, sin_a;
	int dst_s_h, dst_s_w, dst_sr_h, dst_sr_w, dst_srm_h, dst_srm_w;
	
	angle = Angle / 180 * CV_PI;
	cos_a = cos(angle);
	sin_a = sin(angle);
	dst_s_h = (int)(cy*src.rows + 0.5);
	dst_s_w = (int)(cx* src.cols + 0.5);
	dst_sr_h = (int)(fabs(dst_s_h*cos_a) + fabs(dst_s_w*sin_a) + 0.5);
	dst_sr_w = (int)(fabs(dst_s_h*sin_a) + fabs(dst_s_w*cos_a) + 0.5);
	dst_srm_h = fabs(sy)*dst_sr_w + dst_sr_h;
	dst_srm_w = fabs(sx)*dst_sr_h + dst_sr_w;

	int ii = 0, jj = 0;
	double u_src = 0, v_src = 0;

	if (src.channels() == 3)
	{
		dst = cv::Mat::zeros(dst_srm_h, dst_srm_w, CV_8UC3); //RGB图初始
	}
	else
	{
		dst = cv::Mat::zeros(dst_srm_h, dst_srm_w, CV_8UC1);
	}

	Mat M_scale = (Mat_<double>(3, 3) << cx, 0, 0, 0, cy, 0, 0, 0, 1);

	Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5*dst_s_w, 0, -1, 0.5*dst_s_h, 0, 0, 1);
	Mat M_rotate = (Mat_<double>(3, 3) << cos_a, -sin_a, 0, sin_a, cos_a, 0, 0, 0, 1);
	Mat M2 = M_rotate*M_toPhysics;

	Mat M_mis = (Mat_<double>(3, 3) << 1, sx, 0, sy, 1, 0, 0, 0, 1);
	Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5*dst.cols, 0, -1, 0.5*dst.rows, 0, 0, 1);
	Mat M3 = M_toPixel*M_mis;

	Mat M_trans = M3*M2*M_scale;
	Mat M_trans_inv = M_trans.inv();

	Mat dst_uv(3, 1, CV_64F);
	dst_uv.at<double>(2, 0) = 1;
	Mat src_uv(dst_uv);

	//反向映射
	for (ii = 0; ii < dst_srm_h; ++ii)
	{
		for (jj = 0; jj < dst_srm_w; ++jj)
		{
			dst_uv.at<double>(0, 0) = jj;
			dst_uv.at<double>(1, 0) = ii;
			src_uv = M_trans_inv*dst_uv;
			u_src = src_uv.at<double>(0, 0);
			v_src = src_uv.at<double>(1, 0);

			//处理边界问题
			if (int(Angle) % 90 == 0)
			{
				if (u_src < 0) u_src = 0;
				if (v_src < 0) v_src = 0;
				if (u_src>src.cols - 1) u_src = src.cols - 1;
				if (v_src>src.rows - 1) v_src = src.rows - 1;
			}

			//双线性插值
			Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);

		}
	}
	return 1;
}

void main()
{
	Mat src = imread("autumn.jpg", 1),dst;

	//水平、垂直镜像
	int way_mirror = 1;
	//affine_mirrorImg(src, dst, way_mirror);

	//旋转
	double angle_r = 250;
	//int flag = affine_rotateImg(src, dst, angle_r);
	//if (flag == 0)
	//{
	//	return;
	//}

	//平移
	double tx = 50, ty = -50;
//	affine_moveImg(src, dst, tx, ty);

	//尺度变换(缩放)
	double cx = 1.5, cy = 1.5;
	affine_scalingImg(src, dst, cx, cy);

	//错切(偏移)
	double sx = 0.2, sy = 0.2;
//	affine_trans_deviation(src, dst, sx, sy);
//	affine_miscut(src, dst, sx, sy);

	//组合变换 缩放->旋转->错切(即偏移)
//	affine_srm_combImg(src, dst, cx, cy, angle_r, sx, sy);

	// 显示 
	Mat src_resize, dst_resize;
	//affine_scalingImg(src, src_resize, 0.4, 0.3);
	//affine_scalingImg(dst, dst_resize, 0.4, 0.3);

	namedWindow("src", 0);
	namedWindow("dst", 0);
	imshow("src", src);
	imshow("dst", dst);

	waitKey(0);
	system("pause");
}

程序运行结果如下：
注：图片显示部分是截图效果，为了可能看起来不够标准，实际程序运行是没有问题的~
水平镜像

垂直镜像

平移

缩放

错切

旋转

组合变换

参考链接
    博客及程序写作过程中难免出错，欢迎指正~