李宏毅机器学习|生成对抗网络Generative Adversarial Network (GAN)|学习笔记(2)|GAN理论介绍与WGAN
文章目录
- 前言
- 1 Our Objective
- 2 Train
-
- JS divergence is not suitable
- WGAN
-
- Wasserstein distance
- 总结
前言
之前老早就听说了GAN,然后对这个方法还不是很了解,想在今后的论文中应用它。因此来学习下李宏毅讲的GAN,记个笔记。视频地址
1 Our Objective
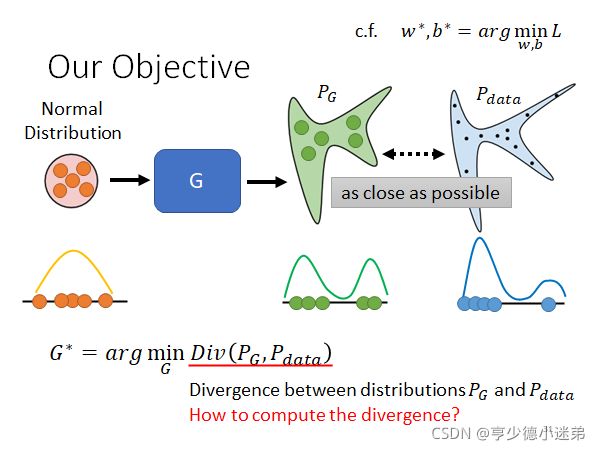
在Generator里面,我们的目标是由Generator产生的分布(叫做 P G P_G PG)和真正的data数据的分布(叫做 P d a t a P_{data} Pdata)越接近越好。
如中间的一维向量而言,输入的是Normal Distribution,Generator产生的分布和真实的data的分布越接近越好。
然后就可以定义相应的最优化数学公式:
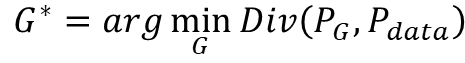
其中的Div指的是 P G P_G PG和 P d a t a P_{data} Pdata之间的差异度。
也即为:

其中的w和b是Generator Network中的weight和bias,L指的是Loss function ,也就是前面提到的 P G P_G PG和 P d a t a P_{data} Pdata之间的差异度。
但是计算这种连续分布之间的Divergence是非常困难的。然后GAN给出了它相应的解法:采样。

也就是我们甚至不需要知道 P G P_G PG和 P d a t a P_{data} Pdata分布的formulation,也可以通过采样的方式来计算这两者之间的差异度。
需要依靠Discriminator的力量了:
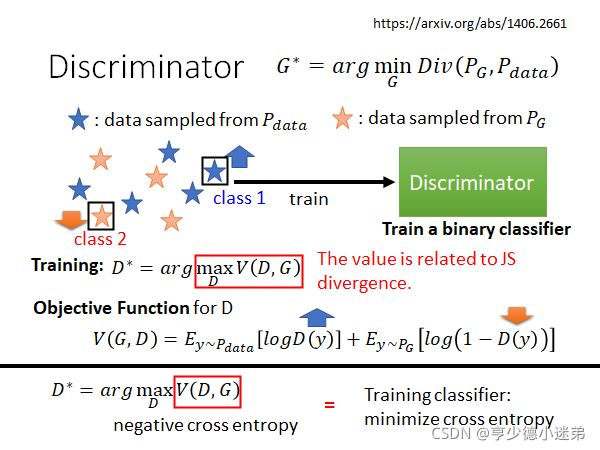
Discriminator训练的目标是:给真正的dara打高分,给生成的data打低分。
等价于:

具体指的:
![]()
从这个公式中看出:最大化

等价于使得从真实datra采样出来的D(y)越大,从Generator生成的y中采样得到的D(y)越小。
上面具体的那个公式,其实是因为最早的GAN的论文作者为了将Discriminator等同于一个binary classifier。因为最大化V(D,G)等价于最小化分类中的交叉熵。
然后这里有一个神奇的地方:

跟JS divergence有关。
前面说到的计算 P G P_G PG和 P d a t a P_{data} Pdata之间的差异度非常困难,现在就可以通过训练Discriminator,
然后利用objective function得到的最大值,这个最大值跟JS divergence有关。
这里不给出具体的证明,然后给了个形象的表达:

简单说,就是当 P G P_G PG和 P d a t a P_{data} Pdata之间的差异度非常小的时候,两者混在一起,很难分辨,这个优化问题就很难,那么解得到的

的值就不会很大,比较小。因此小的Divergence对应小的

如果是差异度非常大的时候,原理是类似的。因此就可以说明

跟JS divergence有关。
因此就可以得到关于Generator和Discriminator求解最优化问题的公式:

简单说,就是我们训练得到的Discriminator的

拿去作为之前提到的差异度。
在最开始介绍GAN的算法的时候说的步骤一和步骤二就是为了解决这个Min Max问题。
也就是先固定G,训练D得到相应公式的最大值。然后固定D,训练G得到使得G产生最小的相应表达式的值。
至于怎样设计不同的objective function(指的是前面说的设计Discriminator的目标函数)得到不同的Divergence,有一篇F GAN的文章列出了相应的表。

2 Train
GAN的训练有很多小技巧(虽然我也不知道),然后李老师这次主要是想讲WGAN。
JS divergence is not suitable

首先是说在大多数的例子当中, P G P_G PG和 P d a t a P_{data} Pdata是不重叠的。原因有二:
1 数据本身的内在性质: 图片其实是高纬空间的低纬manifold(我目前的理解是 一张比如二次元人物的头像是高纬空间中的一个非常特殊的分布,也就是所谓的manifold。)类比于二维空间,图像就是二维空间里面的一条线,而两条线除非完全重合,否则重叠的部分可以忽略不计。
2 采样: 就算 P G P_G PG和 P d a t a P_{data} Pdata有重合的部分,但是我们并不知道两者真实的分布,因此在采样的时候很可能画出一条泾渭分明的线来将两者给完全区分开来。
P G P_G PG和 P d a t a P_{data} Pdata几乎不重叠会给JS divergence带来问题:

当P_G 和 和 和P_{data}$不重叠,JS divergence就会一直为log2。但是如上图所示,就算两者距离变近了,我们也看不出来区别,除非是两者达到了重合。
直觉上就是:训练得到的loss是没用的,因为一直没变嘛,然后只有通过查看每次训练得到的图片来进行。
WGAN
Wasserstein distance

也叫做Earth Mover distance(推土机距离),但是对于更加复杂的distribution,计算Wasserstein distance变得困难了。
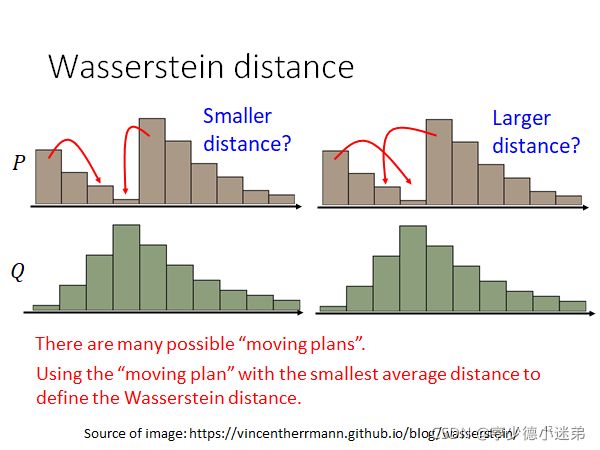
对于复杂的distribution,计算Wasserstein distance方法是:找到所有的moving plans,然后其中最短的平均距离定义为Wasserstein distance。
Wasserstein distance 和 JS divergence的对比:

前者的d会变小,使得在训练的时候能够看出不同的区别。
Wasserstein distance 和进化过程的相似之处:
总结
本文介绍了GAN的理论介绍和WGAN,下一篇将介绍Generator相关内容。



