一、数据清洗:缺失值、异常值和重复值处理
目录
1、数据读取
1.1、使用Pandas库读取excel和csv文件
1.2、使用csv模块读取csv文件
2、处理缺失值
2.1、随机生成缺失值
2.2、定位缺失值
2.3、删除缺失值所在行
2.4、填充缺失值
2.4.1、fillna()方法填充
2.4.1.1、用0填充缺失值
2.4.1.2、用特定值填充特定列
2.4.1.3、用每一列的均值填充
2.4.1.4、用所有数据的均值填充
2.4.2、使用sklearn工具进行填充
2.4.2.1、均值、中位数、众数、常数填充
2.4.2.2、KNN最临近填充
2.4.2.3、多重插补填充
3、处理重复值
3.1、生成重复数据
3.2、删除所有列值相同的重复行
3.3、删除指定列值相同的数据行
4、处理异常值
4.1、箱线图检测异常值
4.2、拉依达准则(3σ准则)检测并处理异常值
1、数据读取
1.1、使用Pandas库读取excel和csv文件
import pandas as pd
# 读取表格数据
df = pd.read_excel('table.xlsx', sheet='sheet1')
df_csv = pd.read_csv('table.csv')
# 查看列名、非空值数量、数据类型
df.info()
# 查看前五行
res = df.head(5)
print(res)1.2、使用csv模块读取csv文件
import csv
# 读取CSV文件
data = []
with open('file.csv', 'r') as file: # 替换 'file.csv' 为您的CSV文件路径
reader = csv.reader(file)
for row in reader:
data.append(row)
# 打印数据
print(data)
2、处理缺失值
2.1、随机生成缺失值
import pandas as pd
import numpy as np
# 随机生成数据
df = pd.DataFrame(np.random.randn(6, 5), columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 假设缺失值
df.iloc[1, 0] = np.nan
df.iloc[2, 3] = np.nan
df.iloc[4, 1] = np.nan
df.iloc[5, 4] = np.nan
print(df)
col1 col2 col3 col4 col5
0.219262 -0.730446 -0.653401 0.360107 0.506213
NaN 0.177408 0.421298 1.294323 0.071185
0.474826 0.689003 0.663731 NaN 1.375225
1.317937 -0.038075 -1.136870 0.172829 -0.008537
-1.082036 NaN -0.252382 1.359398 1.970069
0.487593 -0.645049 -0.740625 2.046696 NaN2.2、定位缺失值
nan_values=df.isnull()
print(nan_values) col1 col2 col3 col4 col5
False False False False False
True False False False False
False False False True False
False False False False False
False True False False False
False False False False True2.3、删除缺失值所在行
df_t = df.dropna()
print(df_t) col1 col2 col3 col4 col5
-0.028936 -0.241142 -1.128235 -0.770114 0.752518
0.747586 1.803407 1.374319 0.835552 1.2538952.4、填充缺失值
2.4.1、fillna()方法填充
2.4.1.1、用0填充缺失值
df.fillna(0, inplace=True)
print(df)
2.4.1.2、用特定值填充特定列
df.fillna({'col5': '3.14'}, inplace=True)2.4.1.3、用每一列的均值填充
mean_values = df.mean() # 计算每一列的均值
df.fillna(mean_values, inplace=True) # 使用均值填充缺失值2.4.1.4、用所有数据的均值填充
mean_value = df.mean().mean()
df.fillna(mean_value, inplace=True)2.4.1.5、用每一行的均值填充
row_means = df.mean(axis=1) # 计算每一行的均值
for row_index, row in df.iterrows():
df.loc[row_index] = row.fillna(row_means[row_index]) # 用每行均值填充该行的缺失值
2.4.2、使用sklearn工具进行填充
2.4.2.1、均值、中位数、众数、常数填充
import pandas as pd
import numpy as np
from sklearn.impute import SimpleImputer
# 随机生成数据
df = pd.DataFrame(np.random.randn(6, 5), columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 假设缺失值
df.iloc[1, 0] = np.nan
df.iloc[2, 3] = np.nan
df.iloc[4, 1] = np.nan
df.iloc[5, 4] = np.nan
print(df)
# 创建SimpleImputer对象
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
# 使用fit_transform方法对DataFrame进行填充缺失值
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
print(df_filled)
2.4.2.2、KNN最临近填充
要使用KNN(K-Nearest Neighbors)最近邻方法填充缺失值,可以使用
KNNImputer类。不过要注意,KNNImputer只能处理数值型数据,而不支持文本或分类数据。
import pandas as pd
import numpy as np
from sklearn.impute import KNNImputer
# 随机生成数据
df = pd.DataFrame(np.random.randn(6, 5), columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 假设缺失值
df.iloc[1, 0] = np.nan
df.iloc[2, 3] = np.nan
df.iloc[4, 1] = np.nan
df.iloc[5, 4] = np.nan
print(df)
# 创建KNNImputer对象,设置临近值为2
imputer = KNNImputer(n_neighbors=2)
# 使用fit_transform方法对DataFrame进行填充缺失值
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
print(df_filled)2.4.2.3、多重插补填充
要使用多重插补(Multiple Imputation)填充缺失值,可以使用
IterativeImputer类。IterativeImputer通过迭代多次估计缺失值,然后进行填充。在每次迭代中,缺失值将被估计并填充,然后被填充的数据将用于估计其他缺失值。这个过程将重复多次,直到收敛为止。
import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer # noqa
from sklearn.impute import IterativeImputer
# 随机生成数据
df = pd.DataFrame(np.random.randn(6, 5), columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 假设缺失值
df.iloc[1, 0] = np.nan
df.iloc[2, 3] = np.nan
df.iloc[4, 1] = np.nan
df.iloc[5, 4] = np.nan
print(df)
# 创建IterativeImputer对象
imputer = IterativeImputer()
# 使用fit_transform方法对DataFrame进行多重插补填充
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
print(df_filled)3、处理重复值
3.1、生成重复数据
import pandas as pd
dat1 = ['A', 4]
dat2 = ['C', 7]
dat3 = ['D', 1]
dat4 = ['C', 7]
dat5 = ['B', 7]
df = pd.DataFrame([dat1, dat2, dat3, dat4, dat5], columns=['col1', 'col2'])
print(df)3.2、删除所有列值相同的重复行
df.drop_duplicates(inplace=True)
print(df)3.3、删除指定列值相同的数据行
df.drop_duplicates(['col1'], inplace=True)
df.drop_duplicates(['col2'], inplace=True)
df.drop_duplicates(['col1', 'col2'], inplace=True)4、处理异常值
4.1、箱线图检测异常值
箱体的长度显示数据的离散程度,箱子越长,数据的离散程度越大。
中位数线位于箱子内部,帮助我们了解数据的中心位置。
Whisker的长度可以帮助我们判断数据的范围,异常值一般在Whisker之外的点上显示。
箱线图的绘制原理如下:
1. 找到数据的最小值和最大值,用一条线(Whisker)连接它们。
2. 计算数据的中位数(Q2),将箱子分为上下两部分。
3. 在上半部分的箱子中,计算第三四分位数(Q3),在下半部分的箱子中,计算第一四分位数(Q1)。
4. 绘制中位数(Q2)的线,连接两个箱子。
5. 在箱子之外,如果有异常值,将其以单独的点表示。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 随机生成数据
df = pd.DataFrame(np.random.randn(6, 5), columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 假设有异常值
df.iloc[1, 0] = 10 # 引入异常值
# 绘制箱线图
plt.figure(figsize=(8, 6))
df.boxplot()
plt.title('Boxplot for Data')
plt.ylabel('Values')
plt.show()
4.2、拉依达准则(3σ准则)检测并处理异常值
拉依达准则(3σ原则)是一种常用的统计方法,用于检测和处理数据中的异常值。该方法基于数据的均值和标准差,通过判断数据点是否位于均值附近的一定范围内,来决定其是否为异常值。
具体步骤如下:
- 计算数据的均值(mean)和标准差(std)。
- 设置一个阈值(通常为3倍标准差,即n=3),即认为超过均值±3倍标准差的数据点为异常值。这个阈值可以根据具体情况进行调整,例如可以选择2倍标准差或4倍标准差作为阈值。
- 对于每个数据点,判断它是否在均值±3倍标准差的范围内。如果在范围内,则被视为正常值;如果不在范围内,则被视为异常值。
- 对于被标记为异常值的数据点,可以选择进行处理。常见的处理方法包括移除异常值、替换为均值或中位数、使用插值法进行填充等。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 随机生成满足正态分布的数据矩阵
np.random.seed(42)
data = np.random.normal(loc=0, scale=1, size=(100, 5))
df = pd.DataFrame(data, columns=['col1', 'col2', 'col3', 'col4', 'col5'])
# 随机插入几个异常值
outliers_indices = np.random.randint(0, 100, 5) # 生成5个随机索引作为异常值位置
df.iloc[outliers_indices, 0] = 10 # 在第一列插入异常值
# 定义检测和移除异常值的函数
def remove_outliers(data, n=3):
mean = data.mean()
std = data.std()
lower_bound = mean - n * std
upper_bound = mean + n * std
data_without_outliers = data[(data >= lower_bound) & (data <= upper_bound)]
return data_without_outliers
# 绘制箱线图,查看原始数据分布情况
plt.figure(figsize=(8, 6))
df.boxplot()
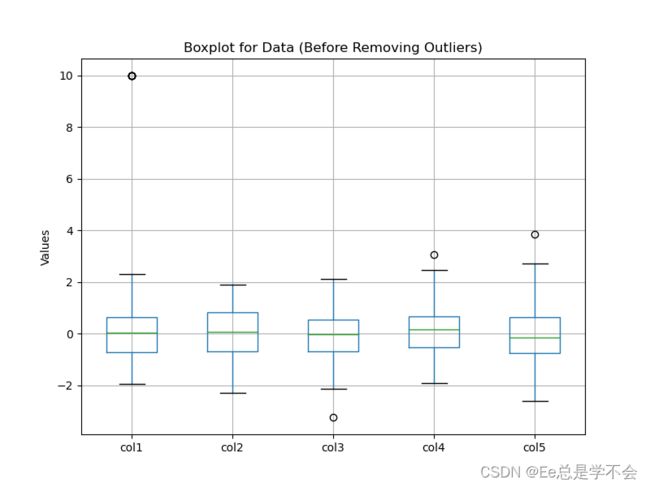
plt.title('Boxplot for Data (Before Removing Outliers)')
plt.ylabel('Values')
plt.show()
# 使用拉依达准则检测并去除异常数据
outliers = {} # 保存被移除的异常值
plt.figure(figsize=(12, 8))
for i, column in enumerate(df.columns):
plt.subplot(2, 3, i + 1)
x = df[column].values
mu = x.mean()
sigma = x.std()
y = (1.0 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-(x - mu) ** 2 / (2 * sigma ** 2))
plt.plot(x, y, label=f'{column} (Original)')
# 使用拉依达准则检测并去除异常值
outliers[column] = df[column][~df[column].isin(remove_outliers(df[column]))].tolist()
df[column] = remove_outliers(df[column])
# 绘制去除异常值后的曲线
good_x = df[column].values
good_mu = good_x.mean()
good_sigma = good_x.std()
good_y = (1.0 / (np.sqrt(2 * np.pi) * good_sigma)) * np.exp(-(good_x - good_mu) ** 2 / (2 * good_sigma ** 2))
plt.plot(good_x, good_y, label=f'{column} (After Removing Outliers)', c='r')
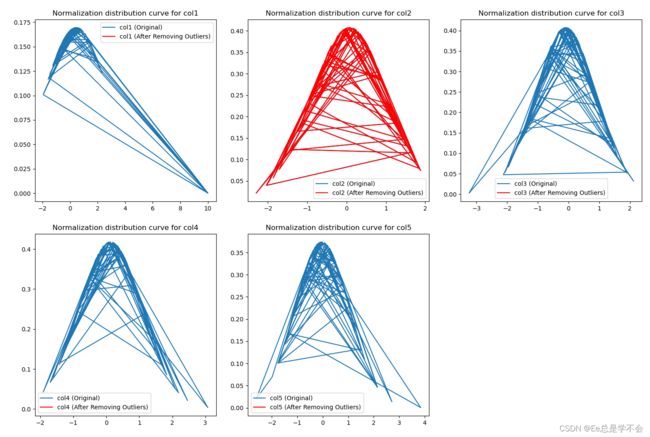
plt.title(f'Normalization distribution curve for {column}')
plt.legend()
plt.tight_layout()
plt.show()
# 输出被移除的异常值
print('The outliers removed:')
for column, values in outliers.items():
print(f'Column {column}: {values}')
# 绘制去除异常值后的数据箱线图
plt.figure(figsize=(8, 6))
df.boxplot()
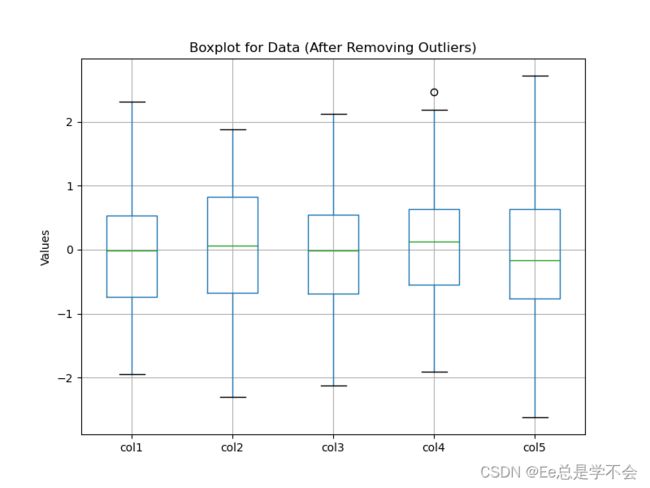
plt.title('Boxplot for Data (After Removing Outliers)')
plt.ylabel('Values')
plt.show()
使用拉依达准则进行异常值检测和处理的优点是简单易懂、计算方便,适用于数据呈现正态分布的情况。然而,它也有一些局限性,例如不适用于非正态分布的数据,对于有时序相关性的数据可能不够敏感,还有可能误判一些正常但极端值较大的数据点。