Acwing算法基础课学习笔记(七)--搜索与图论之DFS&&BFS&&树与图的深度优先遍历&&树与图的广度优先遍历&&拓扑排序

来到第三章的内容，搜索与图论。

排列数字

#include
using namespace std;

int n;      //需要搜索的个数
const int N = 10;

int path[N];    //path[]用于保存路径
bool st[N];     //用于记录 该步是否已经走过，true则表示被用过

void dfs(int u)
{
    if (u == n)        //一条路搜索完成
    {
        for (int i = 0; i < n; i++)  cout << path[i] << ' '; //输出结果        
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++)     //未搜索完成则继续尝试 即一条走到底为止
    {
        if (!st[i])
        {
            st[i] = true;     //标记当前步防止重复
            path[u] = i;   //保存当前路径
            dfs(u + 1);   //进行下一步搜索
            //path[u] = 0;//因为每次都会覆盖path[u]的值，所以也就不用覆盖了
            st[i] = false;    //恢复现场 否则会影响下一条路的搜索
            path[u] = 0;
        }
    }

}
int main()
{
    cin >> n;
    dfs(0);         //从第0个位置开始搜索
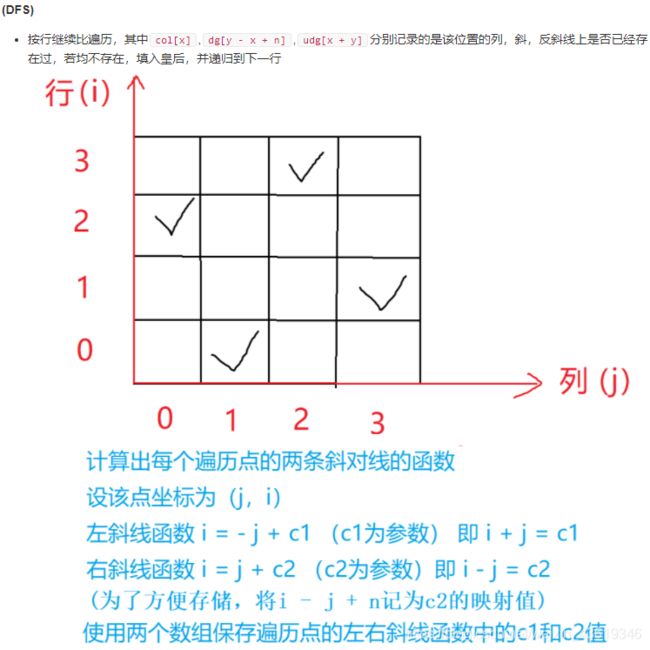
    return 0;
}

n-皇后问题

#include 
using namespace std;
const int N = 20;

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u)
{
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n)
    {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)              udg[n - u + i]，+n是为了保证大于0
        if (!col[i] && !dg[u + i] && !udg[n - u + i])
        {
            col[i] = dg[u + i] = udg[n - u + i] = true;//标记当前步防止重复
            g[u][i] = 'Q';//将皇后放在当前的位置
            dfs(u + 1);//递归到下一行
            g[u][i] = '.';// 恢复现场
            col[i] = dg[u + i] = udg[n - u + i] = false;//依旧是一个完全对称的优美的代码

        }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}

方法二：

// 不同搜索顺序 时间复杂度不同  所以搜索顺序很重要！
#include 
using namespace std;
const int N = 20;

// 因为是一个个搜索，所以加了row
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    // 说明已经放好了n个皇后，表示枚举完 n^2 个了
    if (x == n)
    {
        if (s == n)
        {
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 不放皇后  就往下搜下一个位置
    dfs(x, y + 1, s);

    // 放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
    {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }
}


int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}

走迷宫

#include 
#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;//存储每个点的x和y坐标

const int N = 110;

int n, m; //地图的长宽
int g[N][N]; //存储地图
int d[N][N]; //标记搜索到的点的距离

int bfs()
{
    queue<PII> q; 队列用于BFS操作

    memset(d, -1, sizeof d);  //初始化d
    d[0][0] = 0;//左上角第一个点开始搜索
    q.push({ 0, 0 });//将第一个点入队
    // 方向数组用于对个方向进行尝试，x下方向为正，y右方向为正，顺序为上下左右，bfs常用技巧
    int dx[4] = { -1, 0, 1, 0 }, dy[4] = { 0, 1, 0, -1 }; 

    while (q.size())
    {
        auto t = q.front();//获取队头元素 然后将其出队
        q.pop();

        for (int i = 0; i < 4; i++)
        {
            int x = t.first + dx[i], y = t.second + dy[i];//上右下左四个方向都走一遍

            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//点未出界 该点可走 且未走过
            {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({ x, y });
            }
        }
    }

    return d[n - 1][m - 1];
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> g[i][j];

    cout << bfs() << endl;

    return 0;
}

树的重心

#include 
#include 
#include 

using namespace std;

const int N = 100010; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目

bool st[N]; //记录节点是否被访问过，访问过则标记为true

//a所对应的单链表中插入b  a作为根 所以处在链表的最后
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
    //e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// dfs 框架
/*
void dfs(int u){
    st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[i]) {
            dfs(i);
        }
    }
}
*/

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
    int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点

    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以 用编号为下标 来标记是否被访问过
        if (!st[j]) {
            int s = dfs(j);  // u节点的单棵子树节点数 如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树 的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
    return sum;
}

int main() {
    memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
    cin >> n; //表示树的结点数

    // 题目接下来会输入，n-1行数据，
    // 树中是不存在环的，对于有n个节点的树，必定是n-1条边
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图
    }

    dfs(1); //可以任意选定一个节点开始 u<=n

    cout << ans << endl;

    return 0;
}

图中点的层次

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;
int n, m; //n个节点m条边
int h[N], e[N], ne[N], idx;
int d[N];//存储每个节点离起点的距离  d[1]=0

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int bfs()
{
	memset(d, -1, sizeof d);

	queue<int> q;//存储层次遍历序列 0号节点是编号为1的节点
	d[1] = 0;//存储每个节点离起点的距离
	q.push(1);

	while (q.size())//当我们的队列不为空时
	{
		int t = q.front();//取出队列头部节点
		q.pop();//弹出队列头部节点

		for (int i = h[t]; i != -1; i = ne[i])//遍历t节点的每一个邻边
		{
			int j = e[i];
			if (d[j] == -1)  //如果j没有被扩展过
			{
				d[j] = d[t] + 1;//d[j]存储j节点离起点的距离，并标记为访问过
				q.push(j);//把j结点压入队列
			}
		}
	}

	return d[n];
}

int main()
{
	cin >> n >> m;
	memset(h, -1, sizeof h);
	for (int i = 0; i < m; i++)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	cout << bfs() << endl;

	return 0;
}

有向图的拓扑序列

拓扑图：有向无环图。一个有向无环图一定至少存在一个入度为0的点(可以用反证法证明)。
根据入度的大小给所有的点进行一个排序

这一题是根据入度来进行排序的，我们每次找到入读为0的点，然后把他插入到队列里，然后将这个
点删除，这也就意味着这个点连接的下一个点（可能是多个）的入度就会减1。
这个时候，我们就进入了下一轮。
我们因为前面将一个点删除了，那么它指向的点的入度就会都减去1，所以，就会出现新的点的入度
为0，这个点显然是因为它的入度小，所以它理所应当的排在拓扑序里面在第二位。当前面的一个点没有了被删除了，
那它就要首当其冲了。
举个例子：就是我们给的样例，1的入度为0，2的入度为1，3的入度为2。
因为1的入度为0，所以他很自然的就被放到了队列里，
然后1被删除了，很自然的2的入度变为了0，3的入度变为了1，那我们就把2放入了队列里。
然后2被删除了，很自然3的入度也为0了，那把3也放进去吧。

拓扑排序流程为BFS 流程如下

1. 首先找到第一个入度为0 的点 放入待处理队列，记录答案拓扑数组中 拓扑的必要条件
2. 然后从该点连接的各个点 做以下操作：
   2.1 删除该边后，查看从该点连接的的点的入度
   2.2 如果入度为0 那么该点放入待处理队列，记录答案拓扑数组中， 再次进行BFS 直到待处理队列为空

#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;//依旧是熟悉的邻接表模板
int q[N], d[N];//q是队列，d是每个点的入度表示

int add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool topsort()
{
	int hh = 0, tt = -1;
	for (int i = 1; i <= n; i++)
	{
		if (!d[i])
			q[++tt] = i;//将入度为0的点放入队列里面
	}
	while (hh <= tt)//当队列不为空时
	{
		int t = q[hh++];//找到入度为0 的对头
		//遍历一下以t为头节点的的单链表，给每一个结点都要减去1，并再次找到入度为0的点
		for (int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			d[j]--;//将入度减1
			if (d[j] == 0)	q[++tt] = j;//如果入度为0的话，那就把它放到队列里面
		}
	}

	return tt == n - 1;//如果队尾等于n-1，那么这个序列就是一个拓扑序列
}


int main()
{
	cin >> n >> m;
	memset(h, -1, sizeof h);//给头节点赋值为-1；

	for (int i = 0; i < m; i++)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);//有向图，只用写一个就可以了
		d[b]++;//a，b表示从a进入b，那么我们就给b的入度加上1
	}

	if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i++)	 printf ("%d ", q[i]);//输出答案
    }
    
		

	return 0;
}