蒙特卡罗法求圆周率
本题主要考察函数的嵌套!!!
一.介绍.
蒙特卡罗法:人们把通过随机实验方法进行问题求解的概率算法叫做蒙特卡罗法
函数的嵌套:main函数可以调用其他函数,同样其他函数也可以调用另外的函数,但是在c语言中main函数不能被普通函数调用,在这种函数体内调用其他函数的行为,称为函数的嵌套调用
二.题目介绍.
假设你没有专门练习过飞镖投掷现在让让你随机向圆形靶子投掷飞镖
由数学关系我们可知如下:
由此我们就可以求出圆周率了,下面我们就去通过代码实现它吧!!!
三.代码实现.
补充:由于本人在学多个文件,所以我接下来是通过多个文件实现的,读者当然可以一个文件就行!
我们建立三个文件:
game.h game.c main.c
首先我们先通过main函数(在main.c中)实现主体框架
int main()
{
double pi = 0;//定义圆周率的变量
int n = 0;
scanf("%d", &n);
pi = montecarlopi(n);//montecarlopi蒙特卡罗法函数
printf("圆周率为%lf\n", pi);//输出
return 0;
}接下来我们要开始分析蒙特卡罗法如何求呢?
重点来了!!!
我们现在已经定义了montecarlopi函数,其是用来求解圆周率的,根据我们前面数学计算可知
圆周率=(n/N)*4,那么我们可不可以定义一个函数来实现(n/N)这个过程呢,因此我们定义ratio函数来表达投掷命中率,我们结合生活会发现命中率是与投掷过程息息相关,so,我们就可以在这里定义一个toss函数来实现投掷过程
说干就干,接下来我们通过编程实现:
第一步:
实现montecarlopi函数
game.h;
//montecarlopi函数声明
double montecarlopi(int num);game.c:
//蒙特卡罗法求圆周率
double montecarlopi(int num)
{
return ratio(num) * 4;//ratio函数
}第二步:
此过程只利用game,h和game.c文件:
game.h:
#include
#include
//ratio函数声明
double ratio(int num); game.c:
double ratio(int num)
{
int i = 0;
int sum = 0;//用来表示n
srand((unsigned int)time(NULL));//布置随机数
for (i = 0; i < num; i++)
{
if (1 == toss())//利用toss函数来实现飞镖命中过程
{
sum++;
}
}
return (double)sum / (double)num;
}第三步:
我们要模拟飞标投掷过程了,这是本题难点!!!
前面我们写了以下这个表达式:
if (1 == toss())那么我们是不是就要对toss()是否=1进行判断,此时判断0/1的函数类型为bool型
同时我们要搞懂以下问题:
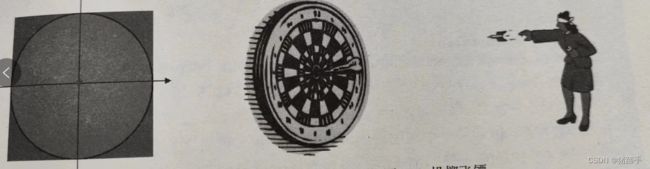
1.如何表示投掷位置?其位置又如何求其是否在靶子上或靶子内部呢?
联系数学知识我们想到建立坐标法,这样既可以简单的表示位置,又可以通过公式来计算其坐标是否在靶子上或靶子内部。
如图(可能有点丑,见谅,刚拉完引体向上,手抖)
2.我们如何来实现坐标的随机?又如何来表示其在x,y的正负半轴呢?
这里很容易想到rand函数,没错,我们可以通过其来实现以上问题
首先,我们来学习下rand函数:
通过上图我们可以发现,如果我们用rand范围(0--RAND_MAX)来表示正负半轴,当其>=2分之RAND_MAX表示正半轴,否者表示负半轴,这样问题迎刃而解
接下来代码走起:
game.h:
#include //bool头文件
#include
//模拟飞镖投掷过程
bool toss(); game.c:
//模拟飞镖投掷过程
bool toss()
{
double x = 0.0;
double y = 0.0;
//x y 表示坐标
double m = (double)(rand() / RAND_MAX);
double n = (double)(rand() / RAND_MAX);
//m用来判断正负半轴,n用来赋值
if (0.5 <= m)
{
x = n;
}
else
{
x = -n;
}
m = (double)(rand() / RAND_MAX);
n = (double)(rand() / RAND_MAX);
if (0.5 <= m)
{
y = n;
}
else
{
y = -n;
}
double z = 0.0;
z = sqrt(x * x + y * y);
if (1 < z)
{
return false;
}
else
{
return true;
}
}四.实验成果
我们发现,不管输入几,其值都为一个固定的数值,这是该算法本身的问题,其值不够精确!!!
最后:
我分享下全部代码:
game.h:
#pragma once
#include
#include
#include
#include //bool头文件
#include
//montecarlopi函数声明
double montecarlopi(int num);
//ratio函数声明
double ratio(int num);
//模拟飞镖投掷过程
bool toss(); game.c:
#define _CRT_SECURE_NO_WARNINGS 1
#include "game.h"
//模拟飞镖投掷过程
bool toss()
{
double x = 0.0;
double y = 0.0;
//x y 表示坐标
double m = (double)(rand() / RAND_MAX);
double n = (double)(rand() / RAND_MAX);
//m用来判断正负半轴,n用来赋值
if (0.5 <= m)
{
x = n;
}
else
{
x = -n;
}
m = (double)(rand() / RAND_MAX);
n = (double)(rand() / RAND_MAX);
if (0.5 <= m)
{
y = n;
}
else
{
y = -n;
}
double z = 0.0;
z = sqrt(x * x + y * y);
if (1 < z)
{
return false;
}
else
{
return true;
}
}main.c:
#define _CRT_SECURE_NO_WARNINGS 1
#include "game.h"
int main()
{
double pi = 0;//定义圆周率的变量
int n = 0;
scanf("%d", &n);
pi = montecarlopi(n);//montecarlopi蒙特卡罗法函数
printf("圆周率为%lf\n", pi);//输出
return 0;
}最后:再见了读者,希望对你有点帮助,欢迎下次再来哈!!!