Polygon zkEVM Merkle tree的circom约束

1. 引言

前序博客有：

• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束

代码见：

• https://github.com/0xPolygonHermez/pil-stark/tree/main/circuits.gl

2. Poseidon哈希circom约束

3. LinearHash circom约束

template LinearHash(nInputs, eSize) {

    signal input in[nInputs][eSize]; //输入in元素数为nInputs*eSize
    signal output out[4];


    var nHashes;

    if (nInputs*eSize <= 4) {
        nHashes = 0;
    } else {
        nHashes = (nInputs*eSize - 1)\8 +1;
    }

    component hash[nHashes];

    if (nInputs*eSize <= 4) {
        var curI=0;
        var curE=0;
        for (var i=0; i<4; i++) {
            if (i0) {
                    hash[i].capacity[k] <== hash[i-1].out[k];
                } else {
                    hash[i].capacity[k] <== 0;
                }
            }
        }

        for (var k=0; k<4; k++) {
            out[k] <== hash[nHashes-1].out[k];
        }
    }
}

4. Merkle tree circom约束

template Merkle(nLevels) { //nLevels表示树高度

    signal input value[4]; //叶子节点数据对应4个Goldilocks元素
    signal input siblings[nLevels][4]; //每个节点哈希值对应4个Goldilocks元素
    signal input key[nLevels]; //key数组表示所在各层的位置
    signal output root[4];

    component hash[nLevels];

    for (var i=0; i0) {
                hash[i].in[k  ] <== key[i]*(siblings[i][k]   - hash[i-1].out[k]) + hash[i-1].out[k];
                hash[i].in[k+4] <== key[i]*(hash[i-1].out[k] - siblings[i][k]  ) + siblings[i][k];
            } else {
                hash[i].in[k] <== key[i]*(siblings[i][k]   - value[k]        ) + value[k];
                hash[i].in[k+4] <== key[i]*(value[k]         - siblings[i][k]  ) + siblings[i][k];
            }
            hash[i].capacity[k] <== 0;
        }
    }

    for (var k=0; k<4; k++) {
        root[k] <== hash[nLevels-1].out[k];
    }

}

5. MerkleHash circom约束

MerkleHash本质为：以values、siblings、key为输入，以root为输出，验证相应的Merkle证明与root是否匹配。
以 s0_merkle1[q] = MerkleHash(1, 2, 2048)=MerkleHash(eSize, elementsInLinear, nLinears) 为例：

• 1）eSize：表示单个数据所需的Goldilocks元素数
• 2）elementsInLinear：表示叶子节点对应的数据数
• 3）nLinears：表示Merkle树中总的节点数

template MerkleHash(eSize, elementsInLinear, nLinears) {
    var nBits = log2(nLinears); //2^11=2048，nBits为Merkle树高度
    assert(1 << nBits == nLinears); //要求nLinears为2的某幂次运算
    signal input values[elementsInLinear][eSize]; //values[2][1]
    signal input siblings[nBits][4]; //Merkle证明路径，每个节点为哈希值对应4个Goldilocks元素。
    signal input key[nBits];  //key数组表示所在各层的位置
    signal output root[4];
	
	 //对 叶子节点下原始数据进行处理，为4个Goldilocks元素。
    component linearHash = LinearHash(elementsInLinear, eSize);

    for (var i=0; i

6. TreeSelector circom约束

TreeSelector约束的根本目的在于：从values[n]数组（数组长度为n）中选出位置key[nLevels]对应的元素out，每个元素的宽度为eSize，即从某队列中选出指定位置的值。
s0_lowValues[q].out[e] === verifyQueries[q].out[e];约束成立的原因在于FRI tree相邻step之间的查询index满足ys[i] = ys[i] % (1 << this.steps[si+1].nBits);。详细可参看Anatomy of a STARK, Part 3: FRI 中“Index Folding”章节：

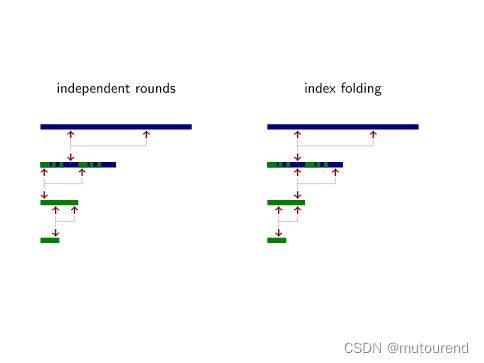
		s0_lowValues[q] = TreeSelector(4, 3) ; //对应get3(proof[si+1].polQueries[i][0], groupIdx)
		//signal input s1_vals[8][48]; // fri 1 tree对应查询点的叶子节点（针对Goldilocks extension 3域），48为对应叶子width, 
                                 // 即： (1 << (starkStruct.steps[s-1].nBits -   starkStruct.steps[s].nBits))*3
        for (var i=0; i<16; i++) {
            for (var e=0; e<3; e++) {
                s0_lowValues[q].values[i][e] <== s1_vals[q][i*3+e];//即FRI下一层的叶子节点数据内容
            }
        }
        // 取FRI下一层的查询位置
        for (var i=0; i<4; i++) {//key数组表示选中位置的二进制表示
            s0_lowValues[q].key[i] <== ys[q][i + 7]; //表示的即为const groupIdx  =Math.floor(ys[i] / nextNGroups);
        }
        // 对应约束F.eq(get3(proof[si+1].polQueries[i][0], groupIdx), ev)
        for (var e=0; e<3; e++) {
            s0_lowValues[q].out[e] === verifyQueries[q].out[e];
        }

其中verifyQueries对应VerifyQuery模板，用于验证FRI中step0的各Merkle tree中查询位置约束关系，对应starkInfo.verifierQueryCode中计算。

以s0_lowValues[q] = TreeSelector(4, 3) ;为例，表示：【数组长度为1 << nLevels。】

template TreeSelector(nLevels, eSize) {

    var n = 1 << nLevels;
    signal input values[n][eSize];
    signal input key[nLevels]; //key数组为选中位置的二进制表示
    signal output out[eSize];

    signal im[n-1][eSize];

    var levelN = n\2;
    var o = 0;
    var lo = 0;
    for (var i=0; i

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理
• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束