【深度学习实验】注意力机制（二）：掩码Softmax 操作

​

一、实验介绍

  注意力机制作为一种模拟人脑信息处理的关键工具，在深度学习领域中得到了广泛应用。本系列实验旨在通过理论分析和代码演示，深入了解注意力机制的原理、类型及其在模型中的实际应用。

本文将介绍将介绍带有掩码的 softmax 操作

二、实验环境

  本系列实验使用了PyTorch深度学习框架，相关操作如下：

1. 配置虚拟环境

conda create -n DL python=3.7 

conda activate DL

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

conda install matplotlib

 conda install scikit-learn

2. 库版本介绍

软件包	本实验版本	目前最新版
matplotlib	3.5.3	3.8.0
numpy	1.21.6	1.26.0
python	3.7.16
scikit-learn	0.22.1	1.3.0
torch	1.8.1+cu102	2.0.1
torchaudio	0.8.1	2.0.2
torchvision	0.9.1+cu102	0.15.2

三、实验内容

0. 理论介绍

a. 认知神经学中的注意力

  人脑每个时刻接收的外界输入信息非常多，包括来源于视
觉、听觉、触觉的各种各样的信息。单就视觉来说，眼睛每秒钟都会发送千万比特的信息给视觉神经系统。人脑通过注意力来解决信息超载问题，注意力分为两种主要类型：

• 聚焦式注意力（Focus Attention）：
  • 这是一种自上而下的有意识的注意力，通常与任务相关。
  • 在这种情况下，个体有目的地选择关注某些信息，而忽略其他信息。
  • 在深度学习中，注意力机制可以使模型有选择地聚焦于输入的特定部分，以便更有效地进行任务，例如机器翻译、文本摘要等。
• 基于显著性的注意力（Saliency-Based Attention）
  • 这是一种自下而上的无意识的注意力，通常由外界刺激驱动而不需要主动干预。
  • 在这种情况下，注意力被自动吸引到与周围环境不同的刺激信息上。
  • 在深度学习中，这种注意力机制可以用于识别图像中的显著物体或文本中的重要关键词。

  在深度学习领域，注意力机制已被广泛应用，尤其是在自然语言处理任务中，如机器翻译、文本摘要、问答系统等。通过引入注意力机制，模型可以更灵活地处理不同位置的信息，提高对长序列的处理能力，并在处理输入时动态调整关注的重点。

b. 注意力机制：

1. 注意力机制（Attention Mechanism）：

   • 作为资源分配方案，注意力机制允许有限的计算资源集中处理更重要的信息，以应对信息超载的问题。
   • 在神经网络中，它可以被看作一种机制，通过选择性地聚焦于输入中的某些部分，提高了神经网络的效率。

2. 基于显著性的注意力机制的近似： 在神经网络模型中，最大汇聚（Max Pooling）和门控（Gating）机制可以被近似地看作是自下而上的基于显著性的注意力机制，这些机制允许网络自动关注输入中与周围环境不同的信息。

3. 聚焦式注意力的应用： 自上而下的聚焦式注意力是一种有效的信息选择方式。在任务中，只选择与任务相关的信息，而忽略不相关的部分。例如，在阅读理解任务中，只有与问题相关的文章片段被选择用于后续的处理，减轻了神经网络的计算负担。

4. 注意力的计算过程：注意力机制的计算分为两步。首先，在所有输入信息上计算注意力分布，然后根据这个分布计算输入信息的加权平均。这个计算依赖于一个查询向量（Query Vector），通过一个打分函数来计算每个输入向量和查询向量之间的相关性。

   • 注意力分布（Attention Distribution）：注意力分布表示在给定查询向量和输入信息的情况下，选择每个输入向量的概率分布。Softmax 函数被用于将分数转化为概率分布，其中每个分数由一个打分函数计算得到。

   • 打分函数（Scoring Function）：打分函数衡量查询向量与输入向量之间的相关性。文中介绍了几种常用的打分函数，包括加性模型、点积模型、缩放点积模型和双线性模型。这些模型通过可学习的参数来调整注意力的计算。

     • 加性模型：$\mathbf{s}(\mathbf{x},\mathbf{q})={\mathbf{v}}^T\tanh (\mathbf{Wx}+\mathbf{Uq})$

     • 点积模型：$\mathbf{s}(\mathbf{x},\mathbf{q})={\mathbf{x}}^T\mathbf{q}$

     • 缩放点积模型：$\mathbf{s}(\mathbf{x},\mathbf{q})=\frac{{\mathbf{x}}^T\mathbf{q}}{\sqrt{D}}$ （缩小方差，增大softmax梯度）

     • 双线性模型：$\mathbf{s}(\mathbf{x},\mathbf{q})={\mathbf{x}}^T\mathbf{Wq}$ （非对称性）

5. 软性注意力机制：

   • 定义：软性注意力机制通过一个“软性”的信息选择机制对输入信息进行汇总，允许模型以概率形式对输入的不同部分进行关注，而不是强制性地选择一个部分。

   • 加权平均：软性注意力机制中的加权平均表示在给定任务相关的查询向量时，每个输入向量受关注的程度，通过注意力分布实现。

   • Softmax 操作：注意力分布通常通过 Softmax 操作计算，确保它们成为一个概率分布。

1. 注意力权重矩阵可视化（矩阵热图）

【深度学习实验】注意力机制（一）：注意力权重矩阵可视化（矩阵热图heatmap）

2. 掩码Softmax 操作

  掩码Softmax操作的用处在于在处理序列数据时，对于某些位置的输入可能需要进行忽略或者特殊处理。通过使用掩码张量，可以将这些无效或特殊位置的权重设为负无穷大，从而在进行Softmax操作时，使得这些位置的输出为0。
  这种操作通常在序列模型中使用，例如自然语言处理中的文本分类任务。在文本分类任务中，输入是一个句子或一个段落，长度可能不一致。为了保持输入的统一性，需要进行填充操作，使得所有输入的长度相同。然而，在经过填充操作后，一些位置可能对应于填充字符，这些位置的权重应该被忽略。通过使用掩码Softmax操作，可以确保填充位置的输出为0，从而在计算损失函数时不会对填充位置产生影响。

a. 导入必要的库

import torch
from torch import nn
import torch.nn.functional as F
from d2l import torch as d2l

b. masked_softmax

  带有掩码的 softmax 操作主要用于处理变长序列，其中填充的元素不应该对 softmax 操作的结果产生影响。

def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)
        

参数解释：

• X: 一个三维张量，表示输入的 logits。

• valid_lens: 一个一维或二维张量，表示每个序列的有效长度。如果是一维张量，它会被重复到匹配 X 的第二维。

函数流程：

1. 如果 valid_lens 是 None，则直接应用标准的 softmax 操作，返回 nn.functional.softmax(X, dim=-1)。

2. 如果 valid_lens 不是 None，则进行以下步骤：

   • 获取 X 的形状 shape。

   • 如果 valid_lens 是一维张量，将其重复到匹配 X 的第二维，以便与 X 进行逐元素运算。

   • 将 X 重塑为一个二维张量，形状为 (-1, shape[-1])，这样可以在最后一个轴上进行逐元素操作。

   • 使用 d2l.sequence_mask 函数，将有效长度外的元素替换为一个很大的负数（-1e6）。这样，这些元素在经过 softmax 后的输出会趋近于零。

   • 将处理后的张量重新塑形为原始形状，然后应用 softmax 操作。最终输出是带有掩码的 softmax 操作结果。

c. 实验结果

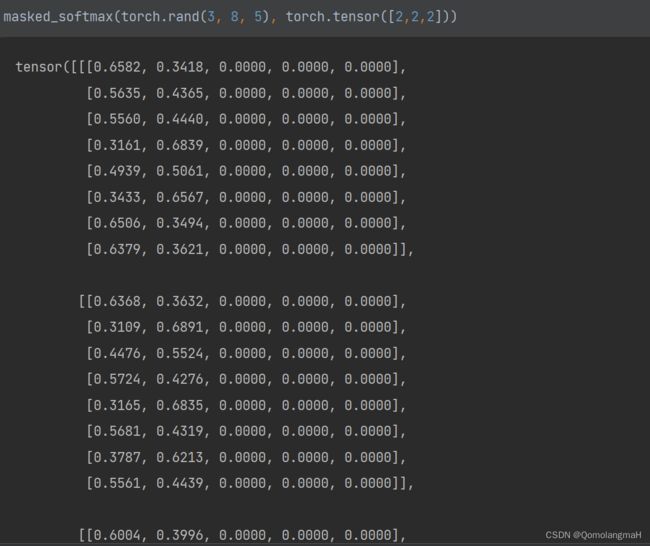
masked_softmax(torch.rand(3, 8, 5), torch.tensor([2, 2, 2]))

• 随机生成了一个形状为 (3, 8, 5) 的 3D 张量，其中有效长度全为 2。

masked_softmax(torch.rand(3, 8, 5), torch.tensor([1, 2, 3]))

• 使用二维张量，为矩阵样本中的每一行指定有效长度

masked_softmax(torch.rand(2, 2, 5), torch.tensor([[1, 3], [2, 4]]))

• 对于形状为 (2, 2, 5) 的 3D 张量
  • 第一个二维矩阵的第一个序列的有效长度为 1，第二个序列的有效长度为 3。
  • 第二个二维矩阵的第一个序列的有效长度为 2，第二个序列的有效长度为 4。