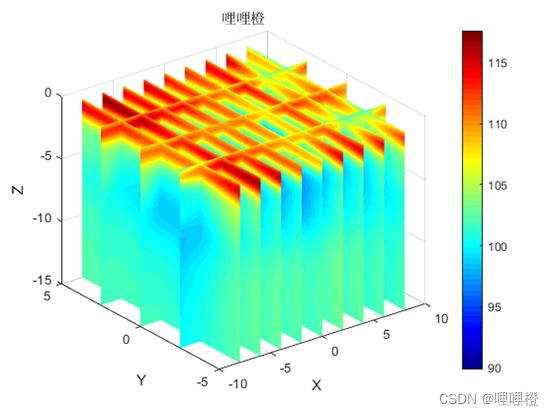
科研笔记第14期——立体切片图绘制

由于V（x,y,z）为三元函数，，无法直接绘制其函数图像，为了观察函数值在空间中的分布情况，故调用slice函数绘制立体切片图。

一、相关函数命令

slice(X,Y,Z,V,xslice,yslice,zslice)为体积数据V绘制切片。指定X,Y和Z作为坐标数据。指定xslice, ysslice和zslice作为切片位置，使用以下形式之一:

（1）若要绘制一个或多个与特定轴正交的切片平面，请将切片参数指定为标量或向量。

（2）要沿着曲面绘制单个切片，请将所有切片参数指定为定义曲面的矩阵。

slice(V,xslice, ysslice,zslice)使用V的默认坐标数据。V中每个元素的(x,y,z)位置分别基于列、行和页索引。

Slice (___，method)指定插值方法，其中method可以是'linear'(默认)，'cubic'或'nearest'。将此选项与以前语法中的任何输入参数一起使用。

二、MATLAB源代码

（1）已知数据点

%% 清空工作区
clear all;
clc;
format long;
%% 读取数据
[num,text,raw]=xlsread('数据.xlsx');
[a,b]=size(num);
%% 输入数据
X=num(:,1);
Y=num(:,2);
Z=num(:,3);
t=num(:,4);
%% 求最大最小值
min_x=min(X);
max_x=max(X);

min_y=min(Y);
max_y=max(Y);

min_z=-15;
max_z=max(Z);

x1 = linspace(min_x, max_x, 200);
y1 = linspace(min_y, max_y, 200);
z1 = linspace(min_z, max_z, 200);  % 对有效数据分割
[X1,Y1,Z1] = meshgrid(x1, y1, z1); % 生成网格数据点
T=griddata(X,Y,Z,t,X1,Y1,Z1,'linear');
%% 定义切片未知
Z_target2=[];
Y_target2=[-2.5 0 2.5];
X_target2=[-8 -6 -4 -2 0 2 4 6 8];
colormap(jet)

slice(X1,Y1,Z1,T,X_target2,Y_target2,Z_target2);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('哩哩橙')

shading interp %插值
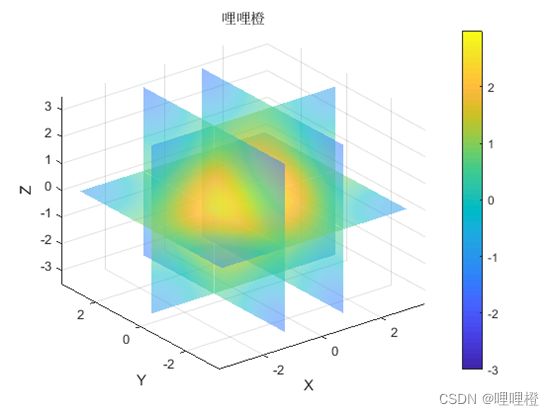
colorbar

（2）已知函数方程

%-------------------插值------------------------------ 
xyz0 = linspace(-pi,pi,30);
[X0,Y0,Z0] = meshgrid(xyz0);
V0 = cos(X0)+cos(Y0)+cos(Z0);
xyz = linspace(-pi,pi,60);
[X,Y,Z] = meshgrid(xyz);
V = cos(X)+cos(Y)+cos(Z);
V1 = interp3(X0,Y0,Z0,V0,X,Y,Z);
err = V1-V;
max(err(:))

%------------------切片图----------------------
slice(X,Y,Z,V,[-1,1],0,0); 
shading interp
alpha(0.5);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('哩哩橙');
set(gca,'color','none');
axis([-3.5, 3.5, -3.5, 3.5, -3.5, 3.5]);
colorbar;

三、运行结果

---

本文内容来源于网络，仅供参考学习，如内容、图片有任何版权问题，请联系处理，24小时内删除。