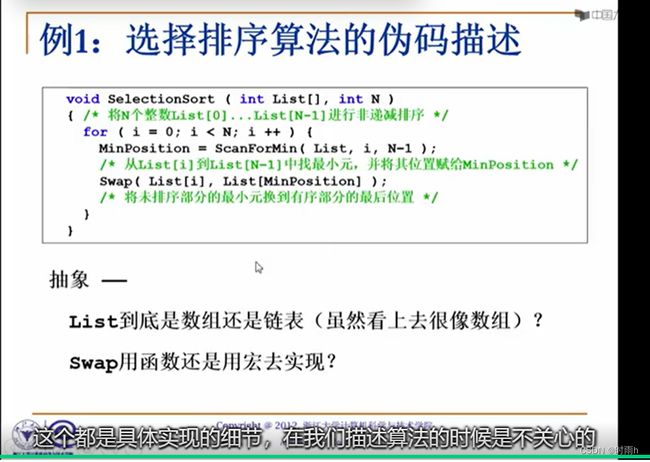
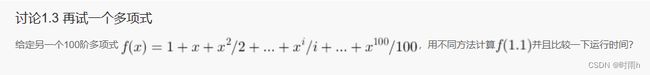浙江大学数据结构陈越 第一讲 数据结构和算法
数据结构

数据结构是计算机科学中用来组织和存储数据的方式。它可以理解为一种组织数据的方式,能够有效地管理和操作数据,以及提供对数据进行存储、检索、更新和删除等操作的方法。常见的数据结构包括数组、链表、栈、队列、树和图等,它们各自适用于不同的应用场景,并且有着不同的特点和操作方式。数据结构的选择对于解决特定的计算问题非常重要,合适的数据结构能够提高算法的效率和性能。
讨论1.1对中等规模、大规模的图书摆放,你有什么更好的建议?
提出这个问题,实际上是想让大家思考,在考虑大规模数据存储的时候会遇到什么问题,以及如何根据功能(也就是关联的算法,最常见的就是插入、查找、删除)需要设计存储方式。
来自课件“讨论1.1对中等规模、大规模的图书摆放,你有什么更好的建议?”
解决问题方法的效率,跟数据的组织方式有关
解决问题方法的效率,跟空间的利用效率有关
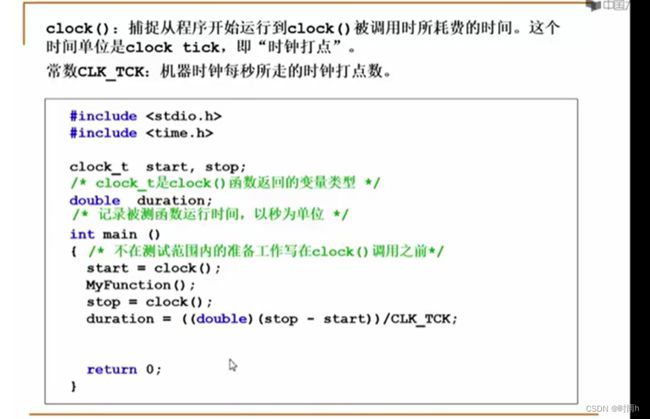
时间复杂度描述了算法解决问题所需的时间量级,而空间复杂度描述了算法解决问题所需的内存空间量级。一个高效的算法应该在时间上尽可能快速地解决问题,并且在空间上尽可能节约内存资源。
有时候,时间复杂度和空间复杂度之间存在折衷关系。例如,某些算法可能通过使用更多的内存空间来降低时间复杂度,或者通过牺牲一定的时间性能来减少内存占用。在实际开发中,需要根据具体的应用场景和需求权衡时间和空间的利用效率。
因此,当评估解决问题方法的效率时,不仅要考虑算法的执行速度,还要考虑所需的内存空间量级。只有在时间和空间两方面都表现出较好的性能时,算法才能被视为高效的解决方法。
当涉及到时间复杂度和空间复杂度时,我们可以通过一个经典的例子来说明。让我们以计算斐波那契数列为例。
首先是使用递归的方法来计算斐波那契数列:
int fibonacci(int n) {
if (n <= 1) {
return n;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}
这个递归实现非常简洁,但是在时间复杂度和空间复杂度上存在一些问题。时间复杂度是O(2^n),因为每次调用都会导致两个更小规模的调用,这使得计算量呈指数级增长。同时,递归调用会占用大量的栈空间,因此空间复杂度也很高。
为了提高效率,我们可以使用迭代的方式来计算斐波那契数列:
int fibonacci(int n) {
int a = 0, b = 1, next, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
next = a + b;
a = b;
b = next;
}
return b;
}
这种迭代的方法时间复杂度为O(n),空间复杂度为O(1)。相比之下,迭代方法在时间和空间上都表现更优秀。
因此,这个例子很好地展示了算法的时间复杂度和空间复杂度对于效率的影响,以及如何通过不同的方法来提高算法的效率。
解决问题的方法效率,跟算法的巧妙程度有关
下面以排序算法为例,展示不同算法的巧妙程度对效率的影响。
假设我们需要对一个整数数组进行升序排序。
首先,我们来看一种简单但效率较低的冒泡排序算法:
void bubbleSort(int arr[], int size) {
for (int i = 0; i < size - 1; i++) {
for (int j = 0; j < size - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
冒泡排序通过不断交换相邻元素的位置来将最大元素逐步冒泡到末尾,时间复杂度为O(n^2)。虽然这个算法实现简单,但效率相对较低,特别是当数组规模较大时。
接下来,我们来看一种更巧妙、效率更高的快速排序算法:
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
快速排序算法通过选择一个基准元素,将小于基准的元素放在左边,大于基准的元素放在右边,然后递归地对左右两部分进行排序。快速排序的平均时间复杂度为O(nlogn),效率相对较高。
从以上例子可以看出,算法的巧妙程度对解决问题方法的效率有很大影响。巧妙的算法能够通过优化计算步骤、减少不必要的操作等方式提高效率。因此,在实际开发中,我们应该选择和设计更巧妙的算法来解决问题,以提高方法的效率。
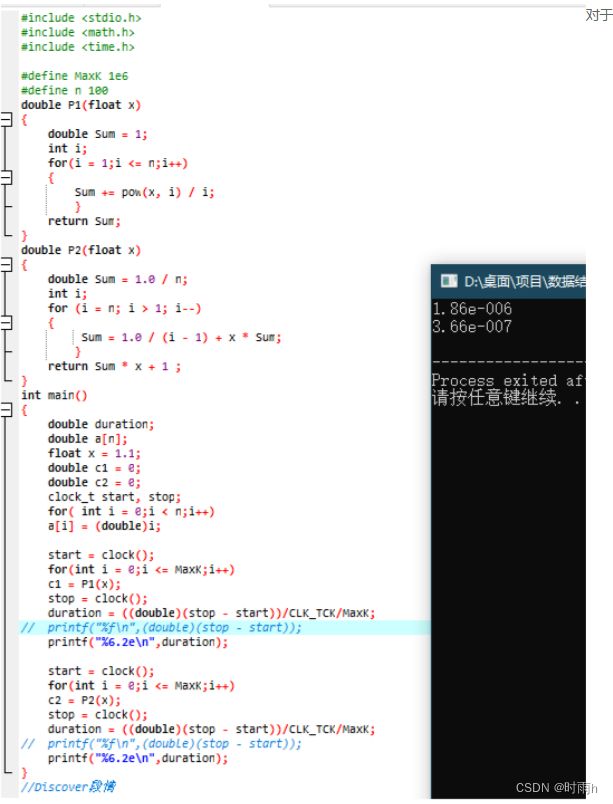
讨论1.3 再试一个多项式
抽象数据类型
抽象数据类型(Abstract Data Type,ADT)是指一个数学模型以及定义在此数学模型上的一组操作。它是一种用于描述数据类型的数学概念,而不涉及具体实现细节。ADT 将数据类型的逻辑特性和对这些特性进行操作的实际实现分离开来,使得用户可以只关注数据类型的逻辑特性而不用关心具体的实现方式。
举例来说,整数可以看作是一个抽象数据类型,我们知道整数具有加法、减法、乘法等操作,以及大小比较等逻辑特性,但我们无需关心整数的具体实现方式。在编程中,我们可以通过定义类或接口来表示抽象数据类型,并在其内部实现相应的操作,从而实现对该抽象数据类型的使用。
常见的抽象数据类型包括栈(stack)、队列(queue)、链表(linked list)、堆(heap)等。这些抽象数据类型都定义了一组操作,比如插入、删除、查找等,而具体的实现可以有多种方式,如数组、链表、树等。
总的来说,抽象数据类型提供了一种高层次的思考方式,使得程序员可以更加专注于数据类型的逻辑特性,而不必过多考虑具体的实现细节。


矩阵是一种常见的数学概念,在抽象数据类型中可以定义如下:
// 矩阵的抽象数据类型定义
template <typename T>
class Matrix {
public:
// 构造函数,创建指定行列的矩阵
Matrix(int rows, int cols);
// 析构函数,释放矩阵内存
~Matrix();
// 获取矩阵的行数
int getRows() const;
// 获取矩阵的列数
int getCols() const;
// 获取矩阵指定位置的元素
T getElement(int row, int col) const;
// 设置矩阵指定位置的元素
void setElement(int row, int col, T value);
// 矩阵加法
Matrix<T> add(const Matrix<T>& matrix) const;
// 矩阵减法
Matrix<T> subtract(const Matrix<T>& matrix) const;
// 矩阵乘法
Matrix<T> multiply(const Matrix<T>& matrix) const;
// 转置矩阵
Matrix<T> transpose() const;
// 打印矩阵
void print() const;
private:
int rows; // 矩阵的行数
int cols; // 矩阵的列数
T** data; // 存储矩阵元素的二维数组指针
};
在上述定义中,我们使用了类模板来定义矩阵的抽象数据类型。通过模板参数 T,可以指定矩阵中元素的类型,比如整数、浮点数等。在类中定义了矩阵的基本操作,包括构造函数、析构函数、获取行列数、获取和设置矩阵元素、矩阵加减法、矩阵乘法、矩阵转置以及打印矩阵等操作。
这样的抽象数据类型定义使得用户可以方便地创建矩阵对象,并对矩阵进行各种操作,而不必关心具体的矩阵实现方式。同时,可以根据实际需要选择不同的矩阵实现方式,比如使用二维数组、使用向量容器等,从而灵活地满足不同场景下的需求。
抽象在软件开发中有什么好处
抽象在软件开发中具有许多好处,如下所示:
-
简化复杂性:抽象可以将复杂的问题和实体简化为高层次的概念和模型。通过隐藏底层的细节,用户只需关注于抽象的特性和行为,而不必了解其具体实现细节。这使得问题更易于理解和处理。
-
提高可维护性:通过抽象,可以将系统分解为模块化的组件,每个组件都有明确定义的接口。这样,当需要进行修改或扩展时,只需关注单个组件,而不会影响其他部分。这种解耦合的设计使得系统更加可维护和可扩展。
-
促进代码重用:抽象可以将通用的功能封装为独立的模块或类,并提供清晰的接口供其他模块使用。通过重用这些抽象的模块,可以避免重复编写相似的代码,提高代码的效率和可靠性。
-
提高代码可读性和可理解性:抽象可以提供更高级别的概念和命名,使代码更易于阅读和理解。通过使用适当的抽象概念和命名,可以使代码更贴近问题领域,并减少冗余的细节,使代码更易于阅读和维护。
-
降低耦合性:通过抽象,不同组件之间的依赖可以通过接口或抽象类来实现,而不是直接依赖于具体实现。这种松耦合的设计有助于减少模块之间的相互依赖,提高系统的灵活性和可扩展性。
总的来说,抽象是软件开发中一种重要的思想和技术,它可以帮助我们更好地理解和处理复杂的问题,并提供可维护、可扩展和高效的代码实现。通过合理使用抽象,可以提高开发效率、降低代码的复杂性,并提升软件质量和可读性。
算法
算法是一系列解决问题或完成任务的明确指令步骤。它是计算机科学和数学领域中的一个重要概念,用于描述解决特定问题的步骤和逻辑。
算法可以用来执行各种任务,如排序、搜索、数据处理、图形处理等。一个好的算法应该具有正确性(能够得出正确的结果)、可读性(易于理解和实现)、高效性(能够在合理的时间内完成任务)和鲁棒性(能够处理各种输入情况)等特点。
常见的算法包括冒泡排序、快速排序、二分查找、深度优先搜索、广度优先搜索等。算法的设计和分析是计算机科学的核心内容之一,它对于解决复杂的计算问题和优化计算过程非常重要。

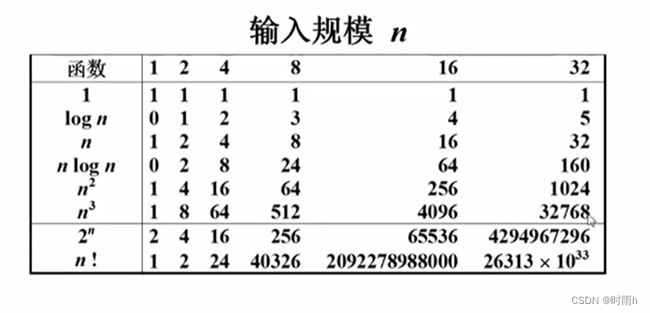
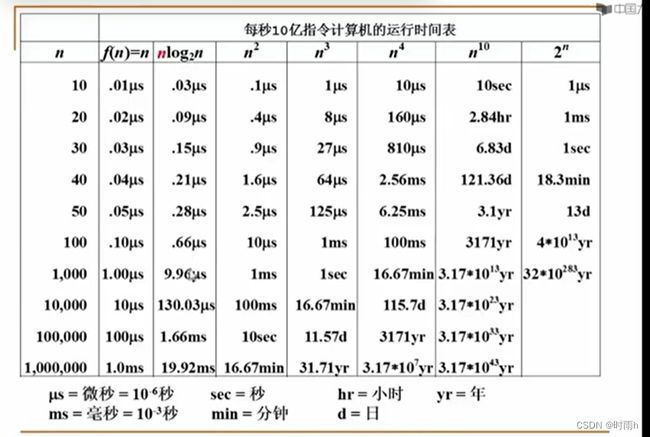
时间复杂度是衡量算法执行时间随输入规模增长而变化的度量。它表示算法执行所需的时间与问题规模之间的关系。
时间复杂度通常用大O符号(O)表示。下面是一些常见的时间复杂度:
-
O(1):常数时间复杂度,表示算法的执行时间不随输入规模变化而变化,即执行时间是固定的。
-
O(log n):对数时间复杂度,表示算法的执行时间随输入规模呈对数增长。
-
O(n):线性时间复杂度,表示算法的执行时间与输入规模成线性关系。
-
O(n log n):线性对数时间复杂度,表示算法的执行时间随着输入规模的增加而增加。
-
O(n^2):平方时间复杂度,表示算法的执行时间随输入规模的平方增长。
-
O(2^n):指数时间复杂度,表示算法的执行时间随输入规模呈指数增长。
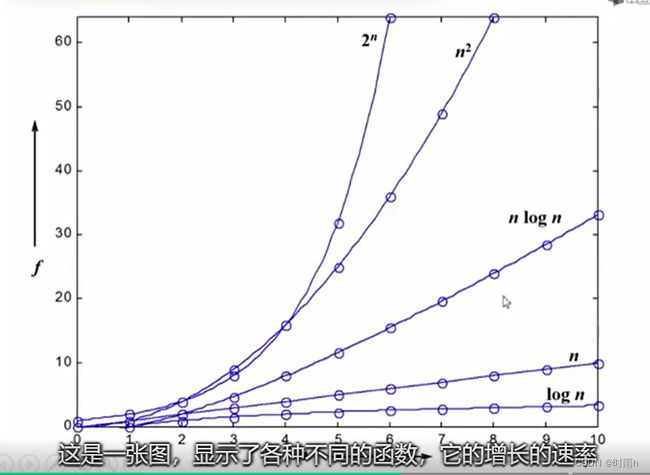
从上述例子可以看出,时间复杂度越小,算法执行的效率越高。在实际应用中,我们希望选择时间复杂度较低的算法来解决问题,以提高程序的执行效率。但需要注意的是,时间复杂度只是一种理论上的分析方法,实际运行时间还受到算法实现的优化程度、硬件环境等因素的影响。
讨论 分析二分法
复杂度的渐进表示法
渐进表示法是用于描述算法时间复杂度的一种标记方法,常用的有大O符号(O)、Ω符号(Ω)和Θ符号(Θ)。它们分别表示最坏情况下、最好情况下和平均情况下的时间复杂度。
-
大O符号(O)表示算法的上界,用来描述最坏情况下的时间复杂度。O(g(n))表示在输入规模为n时,算法的执行时间不会超过g(n)的某个常数倍。例如,O(1)表示常数时间复杂度,O(n)表示线性时间复杂度,O(n^2)表示平方时间复杂度。
-
Ω符号(Ω)表示算法的下界,用来描述最好情况下的时间复杂度。Ω(g(n))表示在输入规模为n时,算法的执行时间不会低于g(n)的某个常数倍。例如,Ω(1)表示常数时间复杂度,Ω(n)表示线性时间复杂度,Ω(n^2)表示平方时间复杂度。
-
Θ符号(Θ)表示算法的紧确界,用来描述平均情况下的时间复杂度。Θ(g(n))表示在输入规模为n时,算法的执行时间在g(n)的某个常数倍范围内。例如,Θ(1)表示常数时间复杂度,Θ(n)表示线性时间复杂度,Θ(n^2)表示平方时间复杂度。
渐进表示法的优势在于它能够忽略算法执行中的常数因素和低阶项,从而更好地反映算法的增长趋势。例如,对于一个算法的时间复杂度为O(5n^2 + 2n + 1),根据渐进表示法,我们可以简化为O(n^2),因为当n足够大时,低阶项和常数因素对总体时间复杂度的影响较小。
需要注意的是,渐进表示法只描述了算法执行时间与输入规模之间的关系,而不考虑其他因素如硬件环境、编程语言等对算法执行时间的影响。因此,在实际应用中,对于具体问题的解决方案选择,还需综合考虑算法的时间复杂度以及其他方面的因素。

应用示例:最大子列和问题
https://blog.csdn.net/liyuanyue2017/article/details/82990246
#include 题目
给定K个整数组成的序列{ N1 _1
1
, N2 _2
2
, …, Nk _k
k
},“连续子列”被定义为{ Ni _{i}
i
, Ni + 1 _{i+1}
i+1
, …, Nj _j
j
},其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
数据1:与样例等价,测试基本正确性;
数据2:102 ^2
2
个随机整数;
数据3:103 ^3
3
个随机整数;
数据4:104 ^4
4
个随机整数;
数据5:105 ^5
5
个随机整数;
输入格式:
输入第1行给出正整数K (≤100000);第2行给出K个整数,其间以空格分隔。
输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数,则输出0。
输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
分析
我想到了三种方法,结合老师给的两种,总共五种方法
先给出 main 函数
int main(){
int n;
int a[100000+5];
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i];
MaxSubseqSum1(n,a);
MaxSubseqSum2(n,a);
MaxSubseqSum3(n,a);
MaxSubseqSum4(n,a);
MaxSubseqSum5(n,a);
return 0;
}
算法一
最直接也是最直观的想法,一个循环控制子列的尾部,内嵌一个循环控制子列的头部,再内嵌一个循环来求解首部到尾部间子列和,每次求解完和更新最大值
/* 方法一:确定子列的首部和尾部,再遍历累加,时间复杂度 O(n^3)*/
int MaxSubseqSum1(int n,int a[]){
int max = 0;
for(int i=0;i<n;i++){ // 控制子列的尾部
for(int k=0;k<i;k++){ // 控制子列的头部
int tmpSum = 0; //临时存放头部到尾部子列和
for(int j=k;j<=i;j++){
tmpSum+=a[j];
}
if(max < tmpSum)
max = tmpSum;
}
}
return max;
}
容易想到,复杂度也高,O ( n 3 ) O(n^3)O(n 3 )
算法二
考虑优化算法一,观察发现每次计算之后的子列和前面的子列都需要重新计算(比如计算 Sum(n+1)需要重新计算 Sum(n)),那我们可以这样优化,想办法能不能将每次计算的结果保存一下,即一个循环控制子列的首部,内嵌一个循环,既控制子列的尾部,也表示该段子列和,叠加一次更新一次最大值
/* 方法二:确定子列的首部,逐个累加,时间复杂度 O(n^2)*/
int MaxSubseqSum2(int n,int a[]){
int max = 0;
for(int i=0;i<n;i++){ // 控制子列的首部
int tmpSum = 0; // 当前子列和
for(int j=i;j<n;j++){ // 控制子列的尾部
tmpSum+=a[j];
if(max < tmpSum)
max = tmpSum;
}
}
return max;
}
把之前控制尾部的循环和求解子列和的循环融合了,复杂度为 O ( n 2 ) O(n^2)O(n 2)
算法三
想法和算法二类似,不过算法二是控制首部,逐渐累加,算法三是控制尾部,逐渐减值。从首部出发可以自然的用一个数保存整段子列和,而从尾部出发则需要额外数组空间来保存子列和,额外数组空间首先保存其前 n 个数之和,然后每次减去当前值形成子列和
/* 方法三:确定子列的结尾,逐个减去子列前的数,时间复杂度 O(n^2)*/
int MaxSubseqSum3(int n,int a[]){
int sum[100000+5];
int max = 0;
sum[0]=a[0];
for(int i=1;i<n;i++) // 预处理保存前 n 个数之和
sum[i]=sum[i-1]+a[i];
for(int i=0;i<n;i++){ // 控制尾部
int tmpSum = sum[i];
for(int j=0;j<=i;j++){ // 控制首部,每一次减去当前值即首尾子列和
if(max < tmpSum)
max = tmpSum;
tmpSum-=a[j];
}
}
return max;
}
把之前控制首部的循环和求解子列和的循环融合了,复杂度为 O ( n 2 ) O(n^2)O(n 2 )
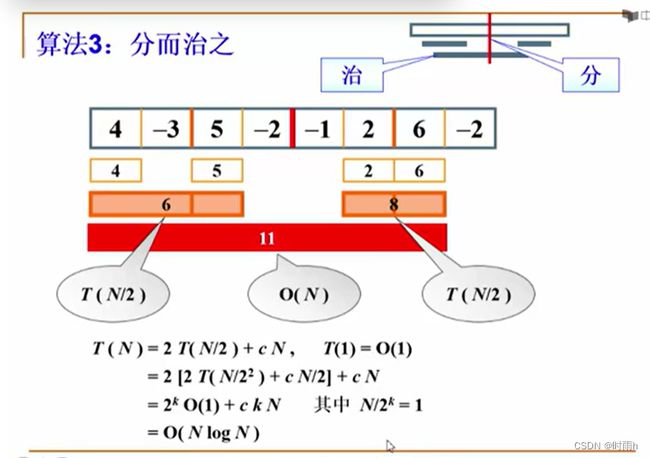
算法四 分而治之
“分治法”,简单来说就是把一个大的问题分解成多个小问题求解,再从所有小的解里面寻求最优解。对于此问题而言,可以把一个大的序列分为两个小的序列,再把小的序列分为更小的两个序列,…,直到每个小序列只有一个数,这就是分的过程,在每个小序列中,会得到:
左边最大子列和(正数即本身,负数即0)
右边最大子列和
横跨划分边界的最大子列和
(比如对于只有 1 | 2 两个数的子列,其左边最大子列和为 1 ,右边最大子列和为 2,而横跨划分边界的最大子列和为 1+2)
此时三者中最大的值就是该小序列的"最大子列和",以此再得到更高层次的"最大子列和",…,最终得到整个问题的最大子列和
/* 方法四:递归分成两份,分别求每个分割后最大子列和,时间复杂度为 O(n*logn)*/
/* 返回三者中最大值*/
int Max3(int A,int B,int C){
return (A>B)?((A>C)?A:C):((B>C)?B:C);
}
/* 分治*/
int DivideAndConquer(int a[],int left,int right){
/*递归结束条件:子列只有一个数字*/
// 当该数为正数时,最大子列和为其本身
// 当该数为负数时,最大子列和为 0
if(left == right){
if(0 < a[left])
return a[left];
return 0;
}
/* 分别递归找到左右最大子列和*/
int center = (left+right)/2;
int MaxLeftSum = DivideAndConquer(a,left,center);
int MaxRightSum = DivideAndConquer(a,center+1,right);
/* 再分别找左右跨界最大子列和*/
int MaxLeftBorderSum = 0;
int LeftBorderSum = 0;
for(int i=center;i>=left;i--){ //应该从边界出发向左边找
LeftBorderSum += a[i];
if(MaxLeftBorderSum < LeftBorderSum)
MaxLeftBorderSum = LeftBorderSum;
}
int MaXRightBorderSum = 0;
int RightBorderSum = 0;
for(int i=center+1;i<=right;i++){ // 从边界出发向右边找
RightBorderSum += a[i];
if(MaXRightBorderSum < RightBorderSum)
MaXRightBorderSum = RightBorderSum;
}
/*最后返回分解的左边最大子列和,右边最大子列和,和跨界最大子列和三者中最大的数*/
return Max3(MaxLeftSum,MaxRightSum,MaXRightBorderSum+MaxLeftBorderSum);
}
int MaxSubseqSum4(int n,int a[]){
return DivideAndConquer(a,0,n-1);
}
时间复杂度 T ( n ) = 2 T ( T 2 ) + c ⋅ n , T ( 1 ) = O ( 1 ) T(n) = 2T(\frac {T}{2}) + c·n ,T(1) = O(1)T(n)=2T(
T
)+c⋅n,T(1)=O(1) ,即 T ( n ) = O ( n l o g n ) T(n) = O(nlogn)T(n)=O(nlogn)
算法五
“贪心法”,即不从整体最优上加以考虑,只做出某种意义上的局部最优解。其实最大子列和与它的首部和尾部都没有关系,我们只关心它当前的大小。当临时和加上当前值为负时,它对之后子列和肯定没有帮助(甚至只会让之后的和更小!),我们抛弃这段临时和将它置0
/* 方法五:直接累加,如果累加到当前的和为负数,置当前值或0,时间复杂度为 O(n)*/
int MaxSubseqSum5(int n,int a[]){
int max = 0;
int tmpSum=0;
for(int i=0;i<n;i++){
tmpSum+=a[i];
if(tmpSum<0){
tmpSum=0;
}else if(max < tmpSum){
max = tmpSum;
}
}
return max;
}
显而易见的,时间复杂度为 O ( n ) O(n)O(n)
Maximum Subsequence Sum
题目
Given a sequence of K integers { N1 _1
1
, N2 _2
2
, …, NK _K
K
}. A continuous subsequence is defined to be { Ni _i
i
, Ni + 1 _{i+1}
i+1
, …, Nj _j
j
} where 1 ≤ i ≤ j ≤ K 1≤i≤j≤K1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.
Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.
Input Specification:
Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.
Output Specification:
For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.
Sample Input:
10
-10 1 2 3 4 -5 -23 3 7 -21
Sample Output:
10 1 4
分析
最大子列和问题加难版
翻译过来就是求一个序列的最大子列和,并输出最大子列和的开头和结尾的数,求最大子列和我们用到了"贪心法",累加当前序列,如果序列和小于 0 就置 0 重新累加,否则更新最大值。
现在的问题是如何记录开头和结尾的数,结尾的数,就是每次更新最大值时记录当时的序列号,该序列号存的值就是结尾的数;而开头的数和每次序列和小于 0 相关,每次序列和清零表示抛弃了这段子序列,之后有新的开始,所以清 0 后下一个序列号里存的就是子序列开头的数,那么如何记录下这个数?对了,更新最大值的时候!每次更新最大值相当于固定一段子序列
最后一个问题就是,当只有一个 0,其余全为负数的情况,按道理应该输出全 0,但是实际输出的是 “0 第一个数 最后一个数”,为了避免这种情况,我们将最大值初值赋为 -1,这样遇到 0 时也能更新最大值
#include二分查找
分析
这题就是写一个二分查找算法的函数接口
基本思路没问题,将要查找的值和当前范围内的中值比较,有三种情况:
要查找的目标值 < 中值,舍弃中值右半部分,缩减范围
要查找的目标值 > 中值,舍弃中值左半部分,缩减范围
要查找的目标值 = 中值,不就找到了吗,直接返回结果
这个查找是一个不确定循环次数的循环,所以用 while,跳出循环的条件是:
找到了,即上面第三种情况,直接 return 即可
找完了,并没有!当界定左范围的值大于界定右范围的值(考虑一下如果相等呢?),表示已经找完,此时返回 NotFound
代码(cpp)
Position BinarySearch( List L, ElementType X ){
Position left = 1;
Position right = L->Last;
while(left<=right){ // 考虑一下这为什么要取等?
Position center = (left+right)/2; //先找中间值
if(L->Data[center] < X){ //比中间值大,X 在右半边
left = center+1;
}else if(X < L->Data[center]){ //比中间值小,X 在左半边
right = center-1;
}else //找到了,直接返回
return center;
}
return NotFound;
}
每次缩减一半范围,所以其复杂度为 O ( l g n ) O(lgn)O(lgn)
二分查找是一种在有序数组中查找特定元素的高效算法。这种搜索算法的工作原理是先确定数组的中间元素,然后将待查找的值与中间元素进行比较。如果待查找的值等于中间元素,则找到了匹配的项;如果待查找的值小于中间元素,则在数组的前半部分继续查找;如果待查找的值大于中间元素,则在数组的后半部分继续查找。通过这种方式,每次比较都能使搜索范围减半,从而实现了较快的搜索速度。
下面是一个用C语言实现的简单的二分查找算法示例:
#include 这段代码演示了如何使用二分查找算法在有序数组中查找特定元素。在main函数中,首先定义了一个有序数组arr和待查找的值x,然后调用binarySearch函数来查找x在数组中的位置。最终根据函数的返回值输出相应的结果。