matlab实践（六）：拉格朗日插值法和Newton插值法

1.拉格朗日插值法

1.1过程

Step1:根据已有给定的 个取值点，求每个取值点对应的拉格朗日基本多项式 ,表示为：

Step2:根据已知的 个取值点，使用第一步中求出的每个取值点对应的拉格朗日基本多项式,然后求已知 个点对应的拉格朗日插值多项式 。其表达式为：

Step3:和原来函数对比

1.2代码实现

 1.2.1计算

function [f,g]=m1(A,x,X)
[n,~]=size(A);
f=1;
g=1;
for i=1:n
    if(A(i,:)~=x)
        f=f*(x(1)-A(i,1));
        g=g.*(X-A(i,1));
    end
end

end
    

1.2.2拟合

clc;clear;
l=1:1:10;
m=l.^2;
A=[l',m'];
[n,~]=size(A);
x=1:0.5:10;
y=0;
for i=1:n
    [f,g]=m1(A,A(i,:),x);
    y=y+A(i,2).*g./f;
end
plot(A(:,1),A(:,2),'k.','Markersize',20);
hold on
plot(x,y,'bo-');
legend('原始函数','拉格朗日拟合');
    

1.3结果

 

2.Newton插值法

2.1过程

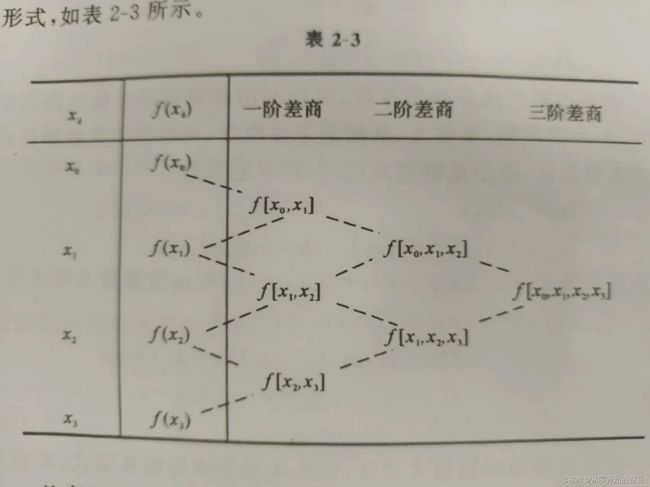
Step1:通过给定插值点的信息，计算 各阶差商

Step2: 代入化简，可得牛顿插值公式为：

2.2代码实现

2.2.1计算各阶差商

function [b1,f1]=n1(A,m)
[n,~]=size(A);
a=A;
a1=a;
for j=1:m
    for i=1:n-1
        b{j}(i)=a(i+1,2)-a(i,2);
        f{j}(i)=(a1(i+1,2)-a1(i,2))/(a1(i+j,1)-a1(i,1));
    end
   
    a(1:n-1,2)=b{j}';
    a1(1:n-1,2)=f{j}';
     n=n-1;     
end
b1=b{m}(1);
f1=f{m}(1);
end

 2.2.2拟合

clc;clear;
% a=randi(10,10,2);
% [B,index]=sort(a(:,1));
% A=[B,a(index,2)];
l=1:1:10;
m=l.^2;
A=[l',m'];
[n,~]=size(A);
x=1:0.5:10;
y1=A(1,2);
y2=A(1,2);
t=0.2;
h=1;
for i=1:2
    [~,f]=n1(A,i);
    h=h.*(x-A(i,1));
%     y1=y1+b.*h;
    y2=y2+f.*h;
end
plot(A(:,1),A(:,2),'k.');
% hold on
% plot(x,y1,'ro');
hold on
plot(x,y2,'bo');
legend('原始函数','Newton插值');
    

2.3结果