C语言学习——整型和浮点型数据在计算机中的储存

这一篇博客主要解决之前留的一个问题，各种数据在计算机到底是怎么储存的。这篇文章就解释一下整型和浮点型数据在计算机中的储存方式。

---

前言

我们知道，计算机是只能够识别二进制的，储存数据时，也只能以二进制的形式存储，那么不同数据在计算机中到底是怎么存储的呢？

---

一、二进制表示

如果想讲清楚数据的储存，先要对二进制有更多的了解。类似于我们日常生活中所使用的的十进制，逢十进一，因此十进制数字只有0~9，二进制数字逢二进一，所以二进制数字只有0和1.

我们表示一个十进制时原理很简单，比如12345就是：5*10⁰+4*10¹+3*10²+2*10³+1*10⁴,
那么同理，对于二进制的1011就是：
1*2⁰+1*2¹+0*2²+1*2³，转化成十进制就是数字11
也就是第N位数的权数是该进制的N-1次方。
对于八进制（十六进制）也是如此，第一位是8（16）的1-1=0次方，后面每一位以此类推。

顺便介绍一下把十进制转化为二进制的方式：短除法

二、整形在计算机中的储存

先介绍无符号整形的储存方式。所谓无符号其实就是只取正数，有符号就是即可以取正数也可以取负数。
假设现在给你8个bit位大小的储存空间

别问我为什么256个数字最大只能表示到255，如果有这个疑问可以找你小学老师给你补补课了。（0~1是几个数字？）
所以现在你知道无符号的int(即 unsigned int)类型数据的最大取值是多少了吧。

然后介绍有符号的，假设现在也是八个比特位。但是为了表示符号，我们规定最高位拿出来当做符号位。真正表示数值大小的是后面的七位。

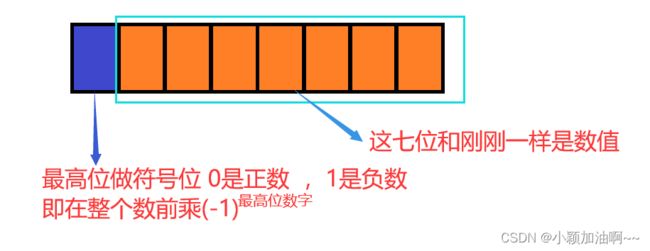
这时候还是表示128个数字，不过这时候是 -128~127 这些数字了
好了，这时候你就知道int 类型可以表示的数据的大小范围了吧。

1.原码，反码，补码

接着介绍这样一组概念。
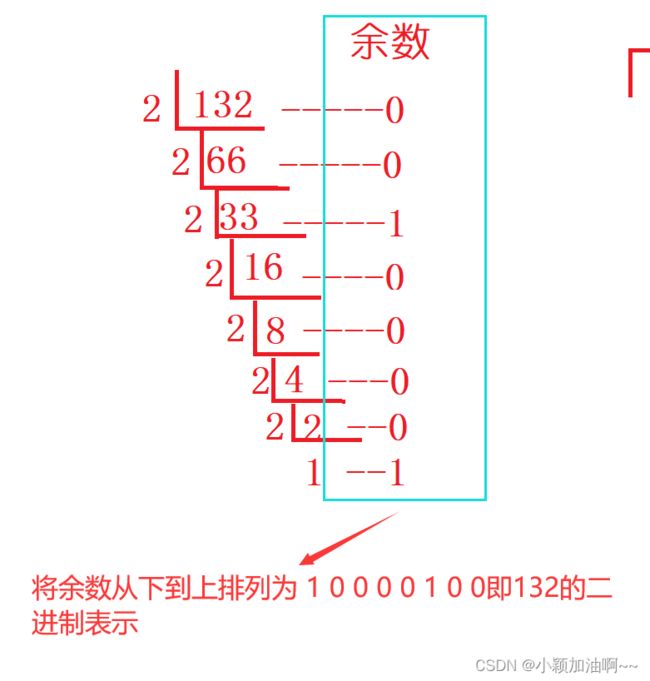
一个数据的二进制有三种形式，我们从十进制直接翻译成二进制后的二进制序列即原码比如上面的十进制的132二进制表述的原码就是：10000100
然后反码要分类讨论，正数的反码是它原码本身，负数的反码是其原码将其除符号位之外的所有位取反（0变1,1变0）举个例子，现在用8个bit位来存数据-12

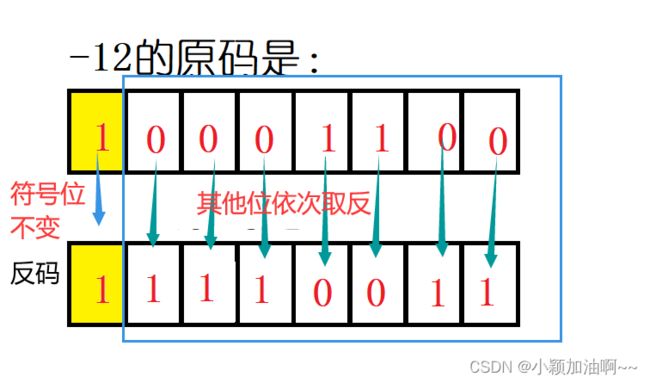
再说补码，对于正数，补码也是其原码本身，负数是反码加一

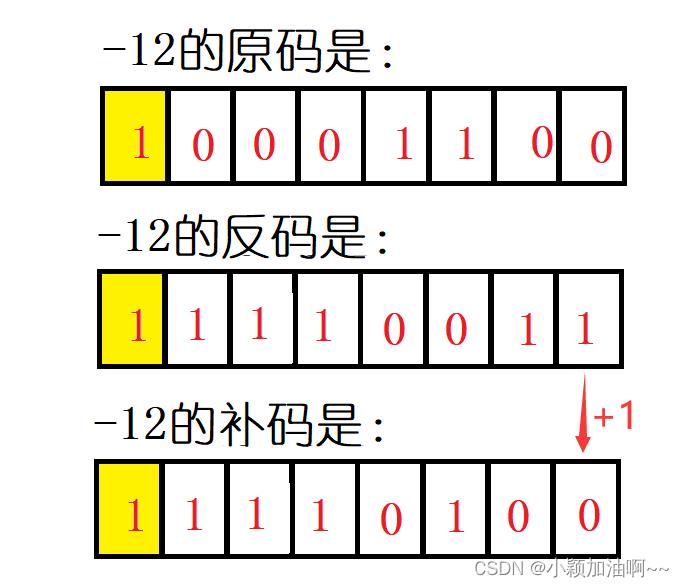
所以我们可以总结为下表：

二进制	正数	负数
原码	短除法得到	短除法得到
反码	和原码相同	原码除符号位外全部取反
补码	和原码相同	反码+1

2.为什么要有反码、补码（不感兴趣可以不看这一部分）

而在计算机中呢，是以补码的形式来存储数据的。为什么呢？为了计算方便（我的理解）因为按照原码的储存方式，将一个整数和一个负数按二进制方式加减得到的结果和实际并不相同，但是用补码就不一样了，你试试-12+13，得到的是不是00000001也就是十进制的1

这个原理你可以类比钟表，1点减去2个小时是11点。
如果要直接算的话，我们先判断1能不能减掉2了，而实际上减不掉，所以要借12个小时（这个和我们小学学减法很像）这样实际上相当于我们是12+1=13点，这时候就可以减去2了，这时候减去2不就是11点嘛。

那么换一种方式思考，我们直接先把12借来。然后直接减你要减的数，就不存在要再借位的情况了（因为时钟最大值就是12，不能减去13）。
现在算一下2点-3小时,5点-10小时分别是几点，看看是不是和你用第一种方式算出来的一样。
但你要问了，那万一是3-2呢？借来12后变成15-2=13了但是钟表没有这个数字啊。确实钟表解决不了，但是计算机可以。
先看这个原理：
比如现在我给你四个比特位表示有符号数其二进制是：
1111
现在加一变成了
10000这个已经是五位了啊，计算机存不下了，怎么办，把多的切掉也就是这个多出来的第五位（最高位）切掉然后变成了0000

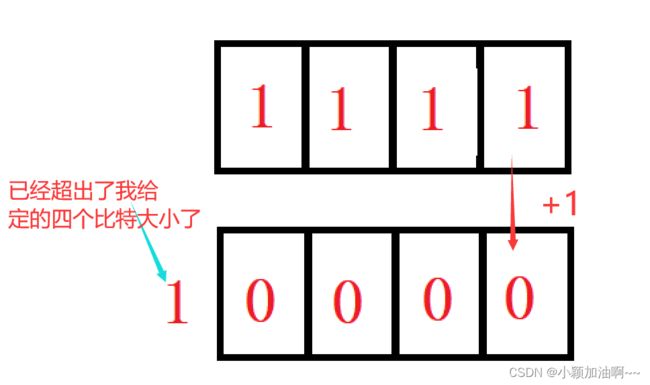
也就是补码的1111和0001相加，结果是0000，我们反推一下原码是啥：

1111最高位是1是负数，所以先减一变成反码1110，然后取反变成原码1001也就是十进制的-1（对这个过程不熟练的回去看原反补码的换算）
0001最高位是0，是正数，直接原码就是0001也就是十进制的1

-1+1=0也就是二进制的
0000 没毛病,这样计算后完全没毛病

而补码和原码的转换正好就是代替这些步骤的过程。

所以科学家们把这个过程直接用取补码的方式代替了，这样其实我们直接就可以使用补码运算省去这个过程

这一部分就不多说了，我一开始也是一头雾水，不过多在草稿纸上写写就明白了。只能说发明计算机的先辈们是真的富有智慧，我们真的是站在巨人的肩膀上，受益无穷。
建议这一部分看完休息几秒，下面也有点烧。

三、浮点数在计算机中的储存

好了，又要开始烧脑了呜呜呜。
浮点数其实就是小数，因为在科学计数法里，小数点是可以移动的，因此叫小数浮点数，比如下图：

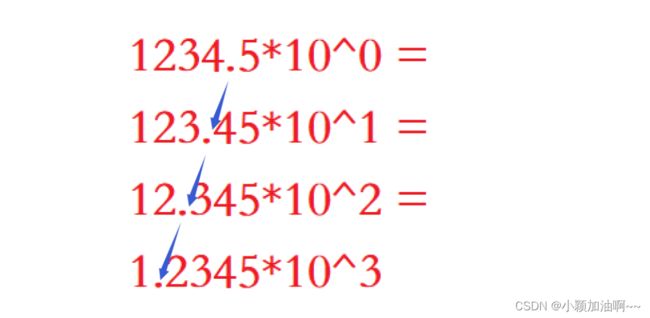
那么在二进制里我们也可以这样玩
比如十进制0.25就是2^-2也就是0*2⁰+0*2^-1+1*2^-2
表示成二进制:0.01
那么8.25怎么表示，该你动脑子了
是不是1000.001呢？
经过很多的数据我们可以发现，可以这样表示浮点数（记得要用二进制的科学计数法把小数点左边的数搞成1，这样小数点的左边数字统一是1了就可以多空出来了一个比特位给M，可以让小数存储地更精确一点）：
（解释下M，比如说8.25吧，二进制是1000.001我们用二进制的科学计数法表示成(1.000001 )*2^-3,M就是小数点后面的000001这样的二进制序列，往下看就知道了）

当结论记吧先~~
根据IEEE 754标准，在32位机器单精度浮点数的空间是这样分配的：

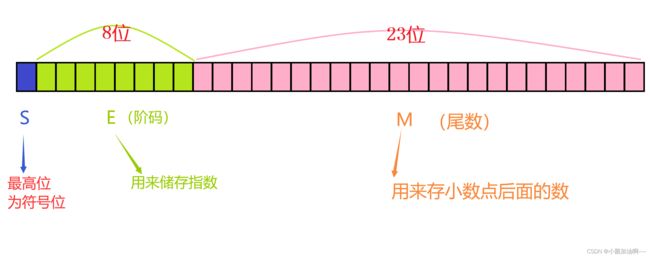
举个例子吧~~
刚刚说的8.25，按二进制表示是1000.001
科学计数法表示成标准形式：1.000001
这时候：

S	e	M
0	-3	00000100000000000000000

这里的-3在一群二进制中显得格外显眼，所以怎么用E的八个比特位来表示-3这个数字呢？我们并不是再1取它的最高位为符号位，而是用移码的方式：八比特位可以表示的最大数是256，我们取一半128，然后令
e = E - 128
注意大写和小写，我们前面的几张图大小写不一样啊！！！公式里的是小写的e！！！内存分配是大写的！！！
然后-3 = 125 - 128，所以这个E = 125，也就是01111101
综上所述
我们得出8.25在计算机中是这样存的：
0 01111101 00000100000000000000000
但是并不是所有的小数都能很精确地存储，但是可以更精确：

双精度浮点数

原理和单精度一样，但是它的E占到10位（这时候e = E - 512），M占到53位，所以更精确了。

---

总结

今天要介绍的就这么多了，配套的专栏：
C语言学习系列博客链接（持续更新中）
第一篇：http://t.csdn.cn/I4Eip
第二篇：http://t.csdn.cn/Brz4y