【Dive into Deep Learning |动手学深度学习（李沐）】4.5权重衰退--学习笔记

权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化。这项技术通过函数与零的距离来衡量函数的复杂度， 因为在所有函数f中，函数f=0（所有输入都得到值0） 在某种意义上是最简单的。

使用均方范数作为硬性限制

通过限制参数的选择范围来控制模型容量，如上图所示，如果参数选择范围变小，模型在空间上就会变得更小，从而模拟出来的曲线更平滑。不过这种方法不常用，更常用的，是下面这种方法。

使用均方范数作为硬性限制

对于每个$\theta$，都可以找到$\lambda$使得之前的目标函数等价于下面的目标函数。

证明过程

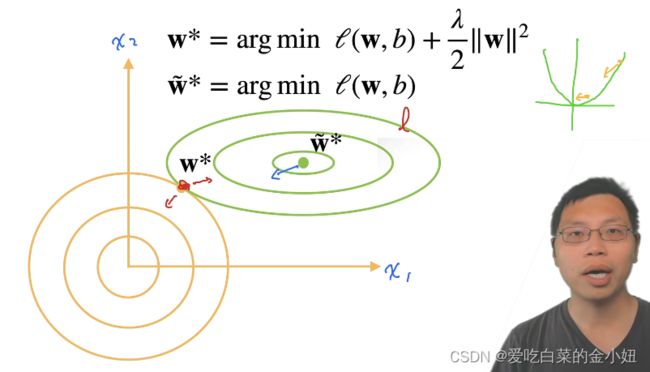
拉格朗日乘子法来证明，拉格朗日乘子法原本是用于解决约束条件下的多元函数极值问题。举例，求f(x,y)的最小值，但是有约束C(x,y) = 0。乘子法给的一般思路是，构造一个新的函数g(x,y,λ) = f(x,y) +λC(x,y)，当同时满足g’x = g’y = 0时，函数取到最小值。这件结论的几何含义是，当f(x,y)与C(x,y)的等高线相切时，取到最小值（这是视频评论给的解释）。所以最优解就从绿圈中心跑到了绿圈和黄圈相切的那个点。
通俗来说，这是两个登高线，绿圈代表原本的损失函数求解过程，黄圈则代表正则项的求解，两个圈相互作用，相互拉扯，在w*处达到平衡。

梯度更新法则

小结

• 权重衰退通过L2正则项使得模型参数不会过大，从而控制模型复杂度。
• 正则项权重是控制模型复杂度的超参数。

代码实现

从零开始

生成数据集

导包

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

生成人造数据集

选择标签是关于输入的线性函数。 标签同时被均值为0，标准差为0.01高斯噪声破坏。 为了使过拟合的效果更加明显，我们可以将问题的维数增加到d=200， 并使用一个只包含20个样本的小训练集。

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5  #训练样本数、测试样本数、输入维度、小批量大小
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05  #定义真实的w、b
train_data = d2l.synthetic_data(true_w, true_b, n_train) #生成训练集
train_iter = d2l.load_array(train_data, batch_size)  #加载训练集
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

这里故意将训练样本选的很小，而测试样本选的较大，就是为了使得模型过拟合。

初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定义L2范数惩罚

L2范数即平方范数，对所有项求平方后再将它们求和。

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

定义训练代码实现

def train(lambd):
    w, b = init_params() #初始化参数
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss  #定义模型为线性模型，损失函数
    num_epochs, lr = 100, 0.003  #迭代次数和学习率
    #动画展示效果
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    #开始迭代训练
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size) #优化函数
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

忽略正则化直接训练

train(lambd=0)

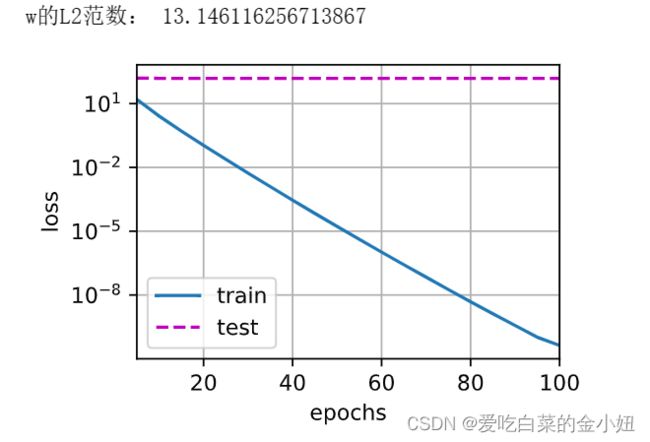
用lambd = 0禁用权重衰减后运行这个代码。 注意，这里训练误差有了减少，但测试误差没有减少， 这意味着出现了严重的过拟合。

使用权重衰减

train(lambd=8)

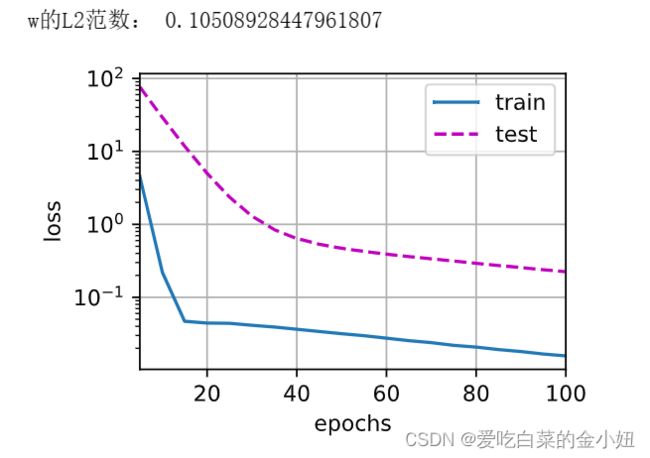
使用权重衰减来运行代码。 注意，在这里训练误差增大，但测试误差减小。 这正是我们期望从正则化中得到的效果。

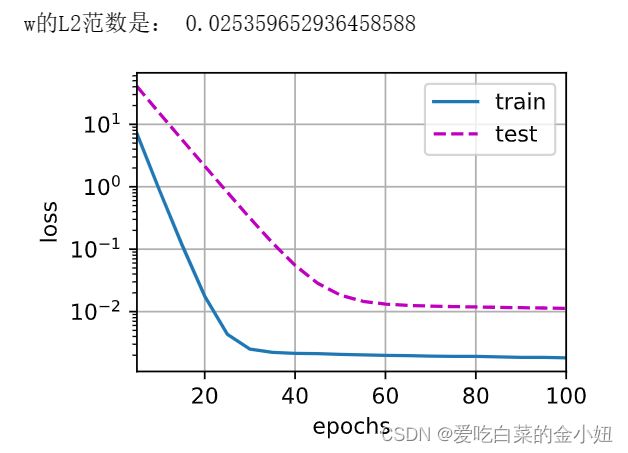
简洁实现

下面的代码中，我们在实例化优化器时直接通过weight_decay指定weight decay超参数。 默认情况下，PyTorch同时衰减权重和偏移。 这里我们只为权重设置了weight_decay，所以偏置参数b不会衰减。

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1)) #定义线性模型
    #初始化参数
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none') #定义均方损失函数
    num_epochs, lr = 100, 0.003  #迭代次数、学习率
    # 偏置参数没有衰减
    trainer = torch.optim.SGD([
        {"params":net[0].weight,'weight_decay': wd},
        {"params":net[0].bias}], lr=lr)
    #动画效果
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    开始训练
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

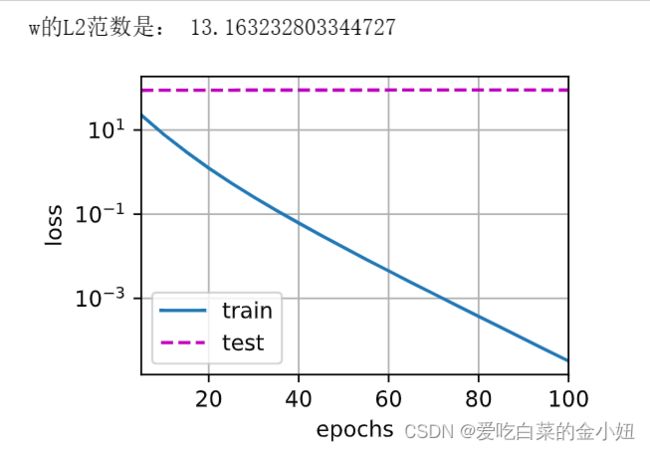
不使用权重衰退

train_concise(0)

使用权重衰退

train_concise(8)

小结

• 正则化是处理过拟合的常用方法：在训练集的损失函数中加入惩罚项，以降低学习到的模型的复杂度。
• 保持模型简单的一个特别的选择是使用惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。
• 权重衰减功能在深度学习框架的优化器中提供。
• 在同一训练代码实现中，不同的参数集可以有不同的更新行为。