洛谷 P1886 滑动窗口 /【模板】单调队列 Java实现
滑动窗口 /【模板】单调队列
题目描述
有一个长为 n n n 的序列 a a a,以及一个大小为 k k k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
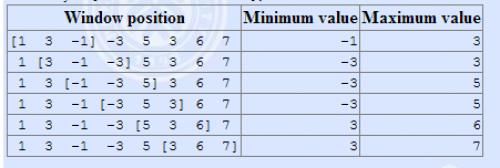
The array is [ 1 , 3 , − 1 , − 3 , 5 , 3 , 6 , 7 ] [1,3,-1,-3,5,3,6,7] [1,3,−1,−3,5,3,6,7], and k = 3 k = 3 k=3。
输入格式
输入一共有两行,第一行有两个正整数 n , k n,k n,k。
第二行 n n n 个整数,表示序列 a a a
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
样例 #1
样例输入 #1
8 3
1 3 -1 -3 5 3 6 7
样例输出 #1
-1 -3 -3 -3 3 3
3 3 5 5 6 7
提示
【数据范围】
对于 50 % 50\% 50% 的数据, 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105;
对于 100 % 100\% 100% 的数据, 1 ≤ k ≤ n ≤ 1 0 6 1\le k \le n \le 10^6 1≤k≤n≤106, a i ∈ [ − 2 31 , 2 31 ) a_i \in [-2^{31},2^{31}) ai∈[−231,231)。
思路:单调队列
这是个裸裸的模板题,求一个固定区域的最大值或者最小值,百分之八十使用单调队列。下面来讲一下什么是单调队列:
拿例题的数来说 [ 1 , 3 , − 1 , − 3 , 5 , 3 , 6 , 7 ] [1,3,-1,-3,5,3,6,7] [1,3,−1,−3,5,3,6,7],窗口大小为3,单调队列的过程如下:
第一步,入队 1 1 1,队列内: 1 1 1
第二步,入队 3 3 3,队列内: 1 , 3 1,3 1,3
第三步,入队 − 1 -1 −1,队列内: − 1 -1 −1
第四步,入队 − 3 -3 −3,队列内: − 3 -3 −3
第五步,入队 5 5 5,队列内: − 3 , 5 -3,5 −3,5
第六步,入队 3 3 3,队列内: − 3 , 3 -3,3 −3,3
第七步,入队 6 6 6,队列内: 3 , 6 3,6 3,6
第八步,入队 7 7 7,队列内: 3 , 6 , 7 3,6,7 3,6,7
规律就是入队一个数,如果是空或者队尾元素小于入队元素,则直接入队。否则,从队尾删除元素,直到符合上面的条件。当然还要出队不属于这个窗口的元素,就像第七步出队了 − 3 -3 −3。
实现代码:
使用Deque可以实现队列的两端插入和删除
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Deque;
import java.util.LinkedList;
public class Main {
private static StreamTokenizer in;
public static void main(String[] args) throws Exception {
in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter pw=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
in.nextToken();int n=(int)in.nval;
in.nextToken();int k=(int)in.nval;
int[] a=new int[n];
Deque<Integer> q=new LinkedList<Integer>();
int[] index=new int[n];
for(int i=0;i<n;i++)
{
in.nextToken();
a[i]=(int)in.nval;
}
int h=0,t=-1;
//模板开始
for(int i=0;i<n;i++)
{
while(!q.isEmpty()&&a[i]<=a[q.peekLast()])
q.pollLast(); //如果不满足单调性则删除队尾元素
q.add(i); //直到满足单调性,入队
if(i-q.peekFirst()>=k) //如果队头元素超出窗口范围则出队
q.pollFirst(); //先入队再判断是否有超出范围的元素,这是因为在入队的时候可能已经将超出的元素删除。就像第四步,入队-3的时候已经删除了所有。
if(i>=k-1) //如果当窗口是满的时候,每次遍历输出队头元素
pw.print(a[q.peekFirst()]+" ");
}
//模板结束
pw.println();
pw.flush();
h=0;
t=-1;
q.clear();
for(int i=0;i<n;i++)
{
while(!q.isEmpty()&&a[i]>=a[q.peekLast()])
q.pollLast();
q.add(i);
if(i-q.peekFirst()>=k)
q.pollFirst();
if(i>=k-1)
pw.print(a[q.peekFirst()]+" ");
}
pw.flush();
}
}
时间复杂度为O(n),效率很高。算法很实用!!!