【背包问题】思路及模板代码

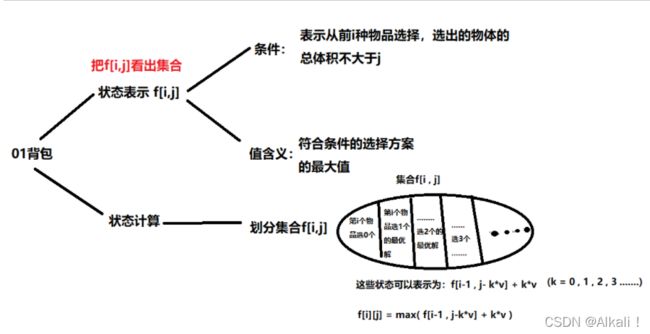
0-1背包问题-每件物品最多只可以使用一次

题目背景

思路

模板代码

#include
#include
using namespace std;
const int N=1010;
int f[N],n,m;
int v[N],w[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=m;j>=v[i];j--)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    printf("%d",f[m]);
    return 0;
}

---

完全背包问题-每件物品可以使用无数次

题目背景

思路

模板代码

#include
using namespace std;
const int N=1010;
int f[N];
int n,m;
int v[N],w[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=v[i];j<=m;j++)  //为什么这里的循环是正序？因为这里省掉的本来的就是第i层的数据，不是原本第i-1层的
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    printf("%d",f[m]);
    return 0;
}

---

多重背包问题1-朴素枚举

题目背景

思路

直接单纯用二维数组硬算，枚举每种情况

模板代码

#include
#include
using namespace std;
const int N=110;
int n,m,s[N],v[N],w[N];
int f[N][N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d%d%d",&v[i],&w[i],&s[i]);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
                f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
    printf("%d",f[n][m]);
    return 0;
}

---

多重背包问题2-二进制优化

题目背景

思路

把任何一个数$N$，利用二进制原理，拆分成$logN$个2的次方的数和一个缺的补数，由这些数，可以自由组合，组合成1~N之间的任何数。
这样，枚举次数就从$N$降低到$logN$,也能等价的枚举出所有情况。

模板代码

#include
#include
using namespace std;
const int N=12010,M=2010;
int v[N],w[N],s[N];
int n,m,cnt;
int f[M];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        int a,b,sum;
        scanf("%d%d%d",&a,&b,&sum);//a是体积，b是价值，s是数量
        int k=1;
        while(k<=sum)             //二进制优化
        {
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s[cnt]=k;
            sum-=k;
            k*=2;
        }
        if(sum>0)     //把最后缺的补到最后就行
        {
            cnt++;
            v[cnt]=a*sum;
            w[cnt]=b*sum;
            s[cnt]=sum;
        }
    }
    n=cnt;
    for(int i=1;i<=n;i++)                  //转化为0-1背包问题求解
        for(int j=m;j>=v[i];j--)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    printf("%d",f[m]);
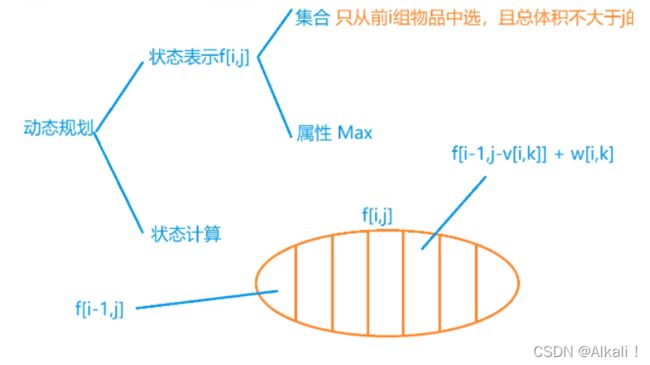
    return 0;
}

---

分组背包问题-每组中最多只能选一个物品

题目背景

思路

模板代码

#include
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N];
int n,m;
int f[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i]);
        for(int j=1;j<=s[i];j++)
            scanf("%d%d",&v[i][j],&w[i][j]);
    }
    for(int i=1;i<=n;i++)
        for(int j=m;j>0;j--)
            for(int k=1;k<=s[i];k++)  //遍历每一组的情况
                if(v[i][k]<=j)
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
    printf("%d",f[m]);
    return 0;
}

---