基于MINST数据集做分类的机器学习项目

机器学习实战

1. 机器学习的基础知识（已完成）
2. 端对端的机器学习项目（已完成）
3. 训练深度神经网络
4. 使用TensorFlow自定义模型和训练
5. 使用TensorFlow加载和预处理数据
6. 使用卷积神经网络的深度计算机视觉
7. 使用RNN和CNN处理序列
8. 使用RNN和注意力机制进行自然语言处理
9. 使用自动编码器和GAN的表征学习和生成学习
10. 强化学习
11. 大规模训练和部署TensorFlow模型

---

---

前言

最常见的有监督学习任务包括回归任务（预测值）和分类任务（预测类）。上一章是回归任务，这一章介绍分类任务。

---

一、MNIST

MNIST数据集是一组由美国高中生和人口调查局员工手写的70000个数字的图片。每张图片都用其代表的数字标记。这个数据集被广为使用，因此也被称作是机器学习领域的“Hello World”。
获取MNIST数据集

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784',version=1)
print(mnist.keys())

dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])
Scikit-Learn加载的数据集通常具有字典结构，包括：

• DESCR键，描述数据集
• data键，包含一个数组，每个实例为一行，每个特征为一列
• target键，包含一个带有标记的数组

X,y = mnist["data"], mnist["target"]
print(X.shape,y.shape)

执行以上的代码看这些数组：

共有七万张图片，每张图片有784个特征。因为图片是28×28像素，每个特征代表了一个像素点的强度，从0（白色）到255（黑色）。
这个过程需要从外网下载数据集，太慢了，而且到后面的程序编写还会加载不出来而报错，所以选择先下载数据集再读取。
下载数据集将其存入一个地址，利用loadmat命令读取。

# mnist = fetch_openml('mnist_784',version=1)   耗时太长
mnist = loadmat('C:/Users/25464/scikit_learn_data/mnist-original.mat')
# print(mnist.keys())
X,y = mnist["data"].T, mnist["label"].T.flatten() # 这个一定要转置一下，因为这里面的行列是反的！！！！！,将y数据展开
y = y.astype(np.uint8)  # 标签是字符，大部分机器学习算法希望是数字，可以把y转换成整数
print(X.shape,y.shape)

运行结果与之前的方式一致，但明显快了很多。

将数据进行混洗。

# 数据混洗
np.random.seed(45)
c = np.column_stack((X,y))  # 将y添加到x的最后一列
c = np.random.permutation(c)   # 打乱顺序
X = c[:,:-1]  # 乱序后的X
y = c[:,-1]   # 同等乱序后的y

可以随机抓取一个实例的特征向量，将其重新形成一个28×28数组，然后用Matplotlib的imshow()函数将其显示出来：

# 随机抓取实例
some_digit = X[0]
some_digit_image = some_digit.reshape(28,28)
plt.imshow(some_digit_image,cmap="binary")
plt.axis("off")
plt.show()
print(y[0])

并与标签y对应，确实是数字8

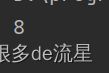
MNIST数据集已经分成训练集（前6万张图片）和测试集（最后一万张图片）

X_train, X_test, y_train, y_test = X[:60000],X[60000:],y[:60000],y[60000:]

二、训练二元分类器

先简化问题，只尝试识别一个数字，比如数字8。这个问题就转化成了建立一个二元分类器，区分：是8和非8。先为此分类任务创建目标向量：

y_train_8 = (y_train == 8 )
y_test_8 = (y_test == 8)

接着挑选一个分类器并开始训练。先选择随机梯度下降（SGD）分类器，使用Scikit-Learn的SGDClassifier类即可。这个分类器的优势是能够有效处理非常大型的数据集，并且适合在线学习。先创建一个SGDClassifier并在整个训练集上进行训练：

sgd_clf = SGDClassifier(random_state=42) # SDGClass在训练时是完全随机的，如果希望得到可复现的结果，需要设置random_state
sgd_clf.fit(X_train,y_train_8)

并用这个训练好的模型对刚刚的实例进行检测

print(sgd_clf.predict([some_digit]))

输出结果为True

三、性能测量

1、 使用交叉验证测量准确率

from sklearn.model_selection import cross_val_score
print(cross_val_score(sgd_clf,X_train,y_train_8,cv=8,scoring="accuracy"))

准确率通常无法成为分类器的首要性能指标，特别是当处理有偏数据集时，例如本例中如果设置所有数都为非8，那么准确率会更高。

2、 混淆矩阵

评估分类器性能的更好方法是混淆矩阵，其总体思路就是统计A类别实例被分为B类别的次数。例如，要想知道分类器将数字3和数字5混淆多少次，只需要通过混淆矩阵的第五行第三列来查看。
要计算混淆矩阵，需要现有一组预测才能将其与实际目标进行比较。因为测试集最好留到项目的最后，所以作为替代，可以使用cross_val_predict()函数，与cross_val_score()函数一样，cross_val_predict()函数同样执行K-折交叉验证，但返回的不是评估分数，而是每个K折叠的预测。
现在可以使用confusion_matrix()函数来获取混淆矩阵。只需要给出目标类别(y_train_8)和预测类别（y_train_pred）。

from sklearn.metrics import confusion_matrix
y_train_pred = cross_val_predict(sgd_clf,X_train,y_train_8,cv=3)
print(confusion_matrix(y_train_8,y_train_pred))

混淆矩阵的行表示实际类别，列表示预测类别。

50379张图片被正确地分到了”非8“类，4203张图片被正确地分到了”是8“类。3760张图片被分到了假负类；1658张图片被分到了假正类。一个完美地分类器只有真正和真负类，所以它的混淆矩阵只会在其对角线上有非零值。
混淆矩阵能提供大量的信息，但有时如果希望指标更简洁一些。正类预测的准确率是一个有意义的指标，它也被称作分类器的精度：

TP是真正类的数量，FP是假正类的数量。做一个单独的正类预测时，分类器会忽略这个正类实例之外的所有内容。因此，精度常常与召回率一起使用，也称为灵敏度或者真正类率：它是分类器正确检测到的正类实例的比例。

FN是假负类的数量。

3、精度和召回率

from sklearn.metrics import precision_score,recall_score
# 精度和召回率
print(precision_score(y_train_8,y_train_pred))  #
print(recall_score(y_train_8,y_train_pred))     #

结果表明，当一张图片是8的时候，只有52.9%的概率是准确的，并且也只有71.7%的数字8被它检测出来了。
因此我们可以把精度和召回率组合成一个单一的指标，称为F1分数。

F1分数是精度和召回率的谐波平均值。正常平均值平等地对待所有值，而谐波平均值会给予低值更高的权重。因此，只有当召回率和精度都很高时，分类器才能得到较高的F1分数。要计算F1分数，只需要调用f1_score即可。

from sklearn.metrics import f1_score
print(f1_score(y_train_8,y_train_pred))

F1分数对那些具有相近的精度和召回率的分类器更为有利。但某些时候，例如训练一个分类器来检测儿童可以放心观看的视频，那么可能更青睐那种拦截了很多好视频（低召回率），但是保留下来的视频都是安全的（高精度）的分类器。但是，不能同时增加精度又减少召回率。这称为精度/召回率权衡。

4、精度/召回率权衡

对于每个实例，SDGClassifier会基于决策函数计算出一个分支，如果该值大于阈值，则将该实例判为正类，否则将其判为负类。阈值越高，召回率越低，但是（通常）精度越高。
Scikit-Learn不允许直接设置阈值，但是可以访问它用于预测的决策分数。不是调用分类器的predict()方法，而是调用decision_function()方法，这种方法返回每个实例的分数，然后就可以根据这些分数，使用任意阈值进行预测了。

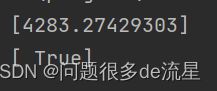
y_scores = sgd_clf.decision_function([some_digit])
print(y_scores)
threshold = 0
y_some_digit_pred = (y_scores>threshold)
print(y_some_digit_pred)

SDGClassifier分类器使用的阈值是0，所以返回结果与predict()方法一样（也就是True）。我们来试试提升阈值

threshold = 8000

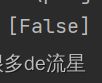
这证明了提高阈值确实可以降低召回率。这张图确实为8，当阈值为0时，分类器可以检测到该图，但是当阈值提高到8000时，就错过了这张图。
那么要如何决定使用什么阈值呢？首先，使用cross_val_predict()函数来获取训练集中所有实例的分数，但是这次需要它返回的是决策分数而不是预测结果，有了这些分数，可以使用precision_recall_curve()函数来计算所有可能的阈值的精度和召回率，使用Matplotlib绘制精度和召回率相对于阈值的函数图。

y_scores = cross_val_predict(sgd_clf,X_train,y_train_8,cv=3,method="decision_function")
precisisons, recalls, thresholds = precision_recall_curve(y_train_8, y_scores)

def plot_precision_recall_vs_threshold(precisions,recalls,thresholds):
    plt.plot(thresholds,precisions[:-1],"b--",label="Precision")
    plt.plot(thresholds,recalls[:-1],"g-",label="Recall")
    plt.legend()
    plt.grid()

plot_precision_recall_vs_threshold(precisisons,recalls,thresholds)
plt.show()

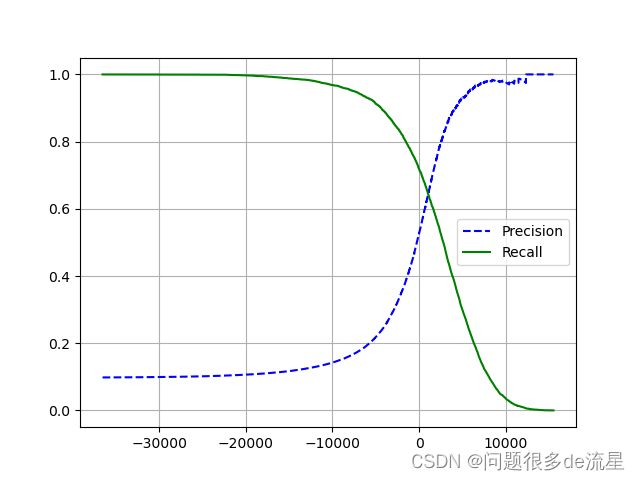
从图中可以看出，召回率从60%向上增加时，精度极度减小。假设决定将精度设为90%。搜索能提供至少90%精度的最低阈值（np.argmax()会给你最大值的第一个索引，在这种情况下，它表示第一个True值）所以最低阈值设置为4178。

threshold_90_precision = thresholds[np.argmax(precisisons >= 0.90)]
print(threshold_90_precision)  # 4177.447970311457
y_train_pred_90 = (y_scores >= threshold_90_precision)
print(y_train_pred_90)

并检查一下这些预测结果的精度和召回率

print(precision_score(y_train_8, y_train_pred_90))
print(recall_score(y_train_8,y_train_pred_90))

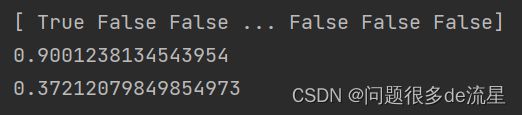
这样就有一个90%精度的分类器了，创建任意一个想要的精度的分类器很容易：只要阈值足够高，然而，如果召回率太低，精度再高，其实也不怎么有用。所以如果有人说需要99%的精度，就应该问召回率是多少。

5、ROC曲线

还有一种经常与二元分类器一起使用的工具，叫做受试者工作特征曲线（检查ROC）。它与精度/召回率曲线非常相似，但绘制的不是精度和召回率，而是真正类率（召回率的另一名称）和假正类率（FPR）。FPR是被错误分为正类的负类实例比率。它等于1减去真负率（TNR），后者是被正确分类为负类的负类实例比率，也称为特异度。因此，ROC曲线绘制的是灵敏度（召回率）和（1-特异度）的关系。
要绘制ROC曲线，首先需要使用roc_curve()函数计算多种阈值的TPR和FPR，然后使用Matplotlib绘制FPR对TPR的曲线。

from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_8, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.grid()

plot_roc_curve(fpr, tpr)
plt.show()

这里再次面临一个折中权衡：召回率（TPR）越高，分类器产生的假正类（FPR）就越多。虚线表示纯随机分类器的ROC曲线、一个优秀的分类器应该离这条线越远越好。

有一种比较分类的的方法是测量曲线下面积（AUC）。完美的分类器的ROC AUC等于1，而纯随机分类器的ROC AUC等于0.5。Scikit-Learn提供计算ROC AUC的函数：

from sklearn.metrics import roc_auc_score
print(roc_auc_score(y_train_8,y_scores))

由于ROC曲线与精度/召回率（PR）曲线非常相似，因此如何决定使用哪种曲线？有一个经验法则是，当正类非常少见或者你更关注假正类而不是假负类时，应该选择PR曲线，反之则是ROC曲线。
现在训练一个随机森林分类器，并比较它和SGD分类器的ROC曲线和ROC AUC分数。
先要获取训练集中每个实例的分数。但是它工作方式不同，随机森林分类器类没有decision_function()方法，相反，它有dict_proba()方法。Scitkit-Learn的分类器通常都会有这两种方法中的一种。dict_proba()方法会返回一个数组，其中每行代表一个实例，每列代表一个类别，意思是某个给定实例属于某个给定类别的概率。
roc_curve()函数需要标签和分数，但是我们不提供分数，而是提供类概率。我们直接使用正类的概率作为分数值，然后绘制ROC曲线，绘制第一条ROC曲线看对比结果。

forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf,X_train,y_train_8,cv=3,method="predict_proba")
y_scores_forest = y_probas_forest[:,1]
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_8,y_scores_forest)
plt.plot(fpr,tpr,"b:",label="SGD")
plot_roc_curve(fpr_forest,tpr_forest,"RandomForest")
plt.legend(loc="lower right")
plt.show()

可以看出随机森林分类器的ROC曲线更好，因此它的ROC AUC分数也更高。

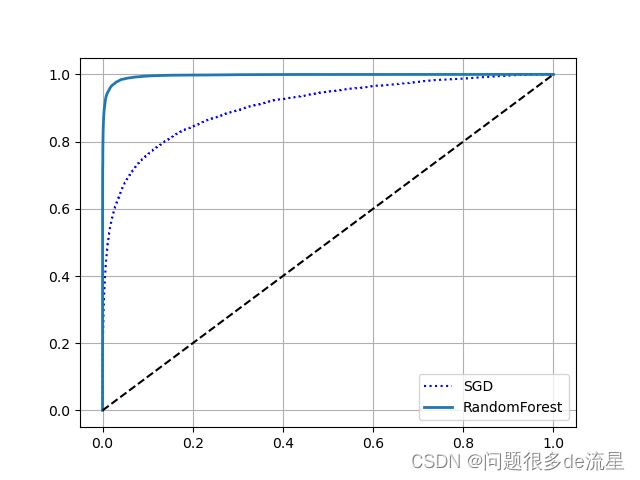
它的ROC AUC分数也更高。

在掌握了如何训练二元分类器，如何选择合适的指标利用交叉验证来对分类器进行评估，如何选择满足需求的精度/召回率权衡，以及如何使用ROC曲线和ROC AUC分数来比较多个模型。接着再试试对数字8之外的检测。

四、多类分类器

二元分类器在两个类中区分，而多类分类器（也称为多项分类器）可以区分两个以上的类。
有一些算法（如随机森林分类器或朴素贝叶斯分类器）可以直接处理多个类。也有一些严格的二元分类器。但是，有多种策略可以让你用几个二元分类器实现多类分类的目的。
要创建一个系统将数字图片分为10类（从0到9），一种方法是训练10个二元分类器，每个数字一个（0-检测器、1-检测器、2-检测器，以此类推）。然后，当你需要对一张图片进行检测分类时，获取每个分类器的决策分数，哪个分类器给分最高，就将其分为哪个类。这称为一堆剩余（OvR）策略，也称为一对多（one-versus-all）。
另一种方法是为每一对数字训练一个二元分类器：一个用于区分0和1，一个区分0和2，一个区分1和2，依次类推。这称为一对一（OvO）策略。如果存在N个类别，那么这需要训练N×（N-1）/2个分类器。对于MNIST问题，这意味着要训练45个二元分类器！当需要对一张图片进行分类，需要运行45个分类器来对图片进行分类，最后看哪个类获胜最多。OvO的主要优点在于，每个分类器只需要用到部分训练集对其必须区分的两个类进行训练。
有些算法（例如支持向量机分类器）在数据规模扩大时表现糟糕。对于这类算法，OvO是一个优先的选择，因为在较小训练集上分别训练多个分类器比在大型数据集上训练少数分类器要快得多。但是对于大多数二元分类器来说，OvR策略还是更好的选择。
Scikit-Learn可以检测到你尝试使用二元分类算法进行多类分类任务，它会根据情况自动运行OvR或者OvO。我们用sklearn.svm.SVC类来试试SVM分类器。

# 支持向量机分类器
svm_clf = SVC()
svm_clf.fit(X_train, y_train)
svm_clf.predict([some_digit])
print(svm_clf.predict([some_digit]))

这段代码使用原始目标类0到9（y_train）在训练集上对SVC进行训练，而不是以”8“和”剩余“作为目标类（y_train_8)。而在内部，Scikit-Learn实际上训练了45个二元分类器，获得它们对图片的决策分数，然后选择了分数最高的类。
可以利用decision_function()方法检查内部运行的原理。

some_digit_scores = svm_clf.decision_function([some_digit])
print(some_digit_scores)
print(np.argmax(some_digit_scores))
print(svm_clf.classes_)
print(svm_clf.classes_[8])

它会返回10个分数，每个类1个，而不再是每个实例返回1个分数。可以发现最高分确实对应数字8这个类别。

当训练分类器时，目标类的列表会存储在class_属性中，按值的大小排序。在本例中，class_数组中每个类的索引正好对应其类本身。但一般来说，不会这么凑巧。
如果想要强制Scikit-Learn使用一对一或者一对多剩余策略，可以使用OneVsOneClaasifier或OneVsRestClassifier类。只需要创建一个实例，然后将分类器传给其构造函数（它甚至不必是二元分类器）。
例如使用OvR策略，基于SVC创建一个多类分类器

ovr_clf = OneVsRestClassifier(SVC())
ovr_clf.fit(X_train,y_train)
ovr_predict = ovr_clf.predict([some_digit])
print(ovr_predict)
print(len(ovr_clf.estimators_))

继续回到SGDClassifier分类器，利用decision_function()获得每个实例分类为每个类的概率，使用cross_val_score()函数评估准确性，利用特征缩放将特征标准化，再次评估其准确性，可以发现经过特征缩放后的准确性更高。

# 训练SGDClassifier或者RandomForestClassifier
sgd_clf.fit(X_train,y_train)
sgd_clf.predict([some_digit])
print(sgd_clf.predict([some_digit]))
print(sgd_clf.decision_function([some_digit]))   # 获得分类器将每个实例分类为每个类的概率列表

# 使用cross_val_score()函数评估准确性
score = cross_val_score(sgd_clf,X_train,y_train,cv=3,scoring="accuracy")
print(score)  #[0.88635 0.8756  0.8846 ]
# # 特征缩放（标准化）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
score = cross_val_score(sgd_clf,X_train_scaled,y_train,cv=3,scoring="accuracy")
print(score) #[0.8965 0.903  0.8992]

五、误差分析

首先看看混淆矩阵，使用cross_val_predict()函数进行预测，然后调用confusion_matrix()函数。
使用Matplotlib的matshow()函数来查看混淆矩阵的图像表示更方便。

y_train_pred = cross_val_predict(sgd_clf,X_train,y_train,cv=3)
conf_mx = confusion_matrix(y_train,y_train_pred)
print(conf_mx)
plt.matshow(conf_mx,cmap=plt.cm.gray)
plt.show()

混淆矩阵很不错，因为大多数图片都在主对角线上，这说明它们被正确分类。


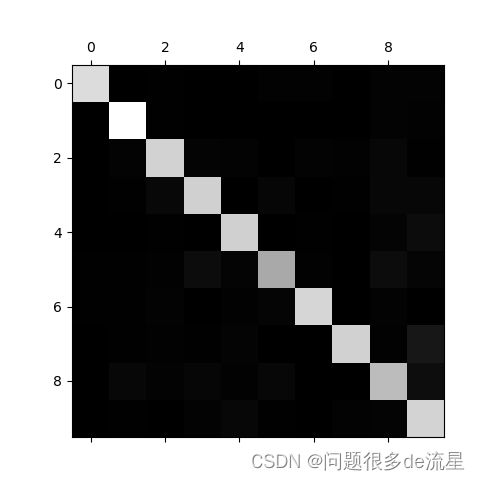
数字5看起来比其他数字稍稍暗一点，这可能意味着数据集中数字5的图片较少，也可能是分类器在数字5上的执行效果不如在其他数字上好。
接下来重点对错误进行分析。首先，需要将混淆矩阵中的每个值除以相应类中的图片数量，这样你比较的就是错误率而不是错误的绝对值（后者对图片数量较多的类不公平），用0填充对角线，只保留错误，重新绘制结果。

# 用0填充对角线，只保留错误，重新绘制结果
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx,cmap=plt.cm.gray)
plt.show()

现在可以清晰地看到分类器产生的错误种类了。每行代表实际类，每列表示预测类。第8列看起来非常亮，说明有很多图片被错误地分类为数字8了。然而，第8行不那么差，告诉你实际数字8被正确分类为数字8。注意，错误不是完全对称的，比如，数字3和数字5经常被混淆（在两个方向上）。
通过上图来看，进数字8的分类错误。例如，可以试着收集更多看起来像数字8的训练数据，以便分类器能够学会将它们与真实的数字区分开来。或者，也可以开发一些新特征来改进分类器——例如，写一个算法来计算闭环的数量（例如，数字8有两个，数字6有一个，数字5没有）。再或者，还可以对图片进行预处理（例如，使用Scikit-Image、Pillow或OpenCV）让某些模式更为突出，比如闭环之类的。

六、多标签分类

在某些情况下，分类器输出可以为多个类。例如，人脸识别的分类器：如果在一张照片里识别出多个人怎么办？应该为识别出来的每个人都附上一个标签。假设分类器经过训练，已经可以识别出三张脸——爱丽丝、鲍勃和查理，那么当看到一张爱丽丝和查理的照片时，它应该输出【1，0，1】这种输出多个二元标签的分类系统称为多标签分类系统。

# 多标签分类
y_train_large = (y_train>=7)
y_train_odd = (y_train%2==1)
y_multilabel = np.c_[y_train_large,y_train_odd] #创建一个数组，其中包含两个数字图片的目标标签：第一个表示数字是否是大数（7、8、9），第二个表示是否为奇数。

knn_clf = KNeighborsClassifier() # 创建一个KNeighborsClassifier实例，支持多标签分类
knn_clf.fit(X_train,y_multilabel) #使用多个目标数组对它进行训练
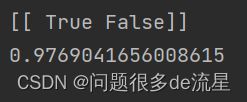
print(knn_clf.predict([some_digit])) # 做一个预测

y_train_knn_pred = cross_val_predict(knn_clf,X_train,y_multilabel,cv=3)
print(f1_score(y_multilabel,y_train_knn_pred,average="macro"))  #计算所有标签的平均F1分数
# 如果设置权重，设置average = "weighted"

# 多标签分类
y_train_large = (y_train>=7)
y_train_odd = (y_train%2==1)
y_multilabel = np.c_[y_train_large,y_train_odd] #创建一个数组，其中包含两个数字图片的目标标签：第一个表示数字是否是大数（7、8、9），第二个表示是否为奇数。

knn_clf = KNeighborsClassifier() # 创建一个KNeighborsClassifier实例，支持多标签分类
knn_clf.fit(X_train,y_multilabel) #使用多个目标数组对它进行训练
print(knn_clf.predict([some_digit])) # 做一个预测

y_train_knn_pred = cross_val_predict(knn_clf,X_train,y_multilabel,cv=3)
print(f1_score(y_multilabel,y_train_knn_pred,average="macro"))  #计算所有标签的平均F1分数
# 如果设置权重，设置average = "weighted"

预测结果是正确的。

七、多输出分类

最后一种分类任务称为多输出-多类分类（或简单地称为多输出分类）。简单来说，它是多标签分类的泛化，其标签也可以是多类的（比如它可以有两个以上可能的值）
构建一个系统去除图片中的噪声。给它输出一张干净的数字图片，与其他MNIST图片一样，以像素强度的一个数组作为呈现方式。这个分类器的输出是多个标签（一个像素点一个标签），每个标签可以有多个值（像素强度范围为0到255）。
先从创建训练集和测试集开始，使用Numpy的randint()函数为MNIST图片的像素强度增加噪声。目标是将图片还原为原始图片。

knn_clf = KNeighborsClassifier() # 创建一个KNeighborsClassifier实例，支持多标签分类
# 多输出分类
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test

# 通过训练分类器，清洗图片

def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    plt.axis("off")


some_index = 0
plt.subplot(121)
plot_digit(X_test_mod[some_index])
plt.subplot(122)
plot_digit(y_test_mod[some_index])

knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
plt.show()

左边图片是加了噪声的图片，右边是每加噪声的图片

这个是代表经过模型训练后处理后的噪声图片。

---

练习题

1、为MNIST数据集构建一个分类器，并在测试集上达成97%的准确率

# 练习题------>为MINST数据集构建一个分类器，并在测试集上达到97%准确率
knn_clf = KNeighborsClassifier() # 创建一个KNeighborsClassifier实例，支持多标签分类
# 网格搜索超参数
param_grid = [{'weights':['uniform', 'distance'],'n_neighbors':[2,4,6,8]}]
grid_search = GridSearchCV(knn_clf,param_grid,cv=3,scoring='neg_mean_squared_error',return_train_score=True)
print(grid_search.best_estimator_)   # 最佳预估器
grid_search.fit(X_train,y_train)
knn_clf_pred = grid_search.predict(X_test)
print(accuracy_score(y_test,knn_clf_pred))

准确率达到了97.5%，最终估算器是n_neighbors=4,weights=distance。

2、写一个可以将MNIST图片向任意方向（上、下、左、右）移动一个像素的功能。然后对训练集中的每张图片，创建四个位移后的副本（每个方向一个），添加到训练集。最后，在这个扩展过的训练集上训练模型，测量其在测试集上的准确率。

# 练习题2------->写一个可以将MNIST图片向任意方向（上、下、左、右）

def shift_image(image, dx, dy):
    image = image.reshape((28,28))
    shiftd_image = shift(image,[dy,dx],cval=0,mode="constant")
    return shiftd_image.reshape([-1])

image = X_train[1000]
shifted_image_down = shift_image(image,0,5)
shifted_image_left = shift_image(image,-5,0)
shifted_image_up = shift_image(image,0,-5)
shifted_image_right = shift_image(image,5,0)

plt.figure(figsize=(12,3))
plt.subplot(131)
plt.title("Original",fontsize=14)
plt.imshow(image.reshape(28,28),interpolation="nearest",cmap="Greys")
plt.subplot(132)
plt.title("Shifted down",fontsize=14)
plt.imshow(shifted_image_down.reshape(28,28),interpolation="nearest",cmap="Greys")
plt.subplot(133)
plt.title("Shifted left",fontsize=14)
plt.imshow(shifted_image_left.reshape(28,28),interpolation="nearest",cmap="Greys")
plt.show()
plt.title("Shifted up",fontsize=14)
plt.imshow(shifted_image_up.reshape(28,28),interpolation="nearest",cmap="Greys")
plt.show()
plt.title("Shifted right",fontsize=14)
plt.imshow(shifted_image_right.reshape(28,28),interpolation="nearest",cmap="Greys")
plt.show()

X_train_augmented = [image for image in X_train]
y_train_augmented = [label for label in y_train]

for dx,dy in ((1,0),(-1,0),(0,1),(0,-1)):
    for image,label in zip(X_train,y_train):
        X_train_augmented.append(shift_image(image,dx,dy))
        y_train_augmented.append(label)

X_train_augmented = np.array(X_train_augmented)
y_train_augmented = np.array(y_train_augmented)

shuffle_idx = np.random.permutation(len(X_train_augmented))
X_train_augmented = X_train_augmented[shuffle_idx]
y_train_augmented = y_train_augmented[shuffle_idx]

knn_clf = KNeighborsClassifier(**grid_search.best_params_)
print(grid_search.best_params_)
knn_clf.fit(X_train_augmented,y_train_augmented)

y_pred = knn_clf.predict(X_test)
print(accuracy_score(y_test,y_pred))

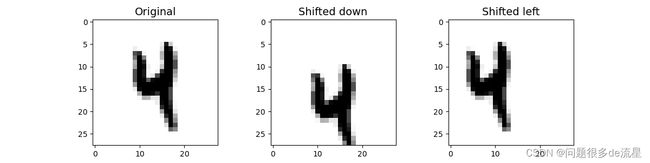
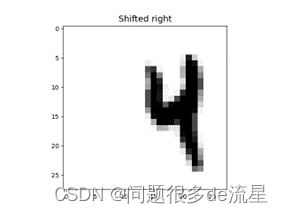
以上五张图片分为原始图片，以及向四个方向平移的图片。

最后输出结果，最佳参数是n_neighbors=4，weights=‘distance’。
准确率为98.14%。
模型的表现甚至变得更好了！这种人工扩展训练集的技术称为数据增广或训练集扩展。
3、创建一个垃圾邮件分类器（更具挑战性的练习）：